- This is an assessment test.
- These tests focus on the basics of Maths and are meant to indicate your preparation level for the subject.
- Kindly take the tests in this series with a pre-defined schedule.
Basic Maths: Test 38
Congratulations - you have completed Basic Maths: Test 38.You scored %%SCORE%% out of %%TOTAL%%.Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
Which one of the following does not divide$\left( {{5}^{2430}}-1 \right)$?
24 | |
124 | |
624 | |
3124 |
Question 1 Explanation:
When n is odd or even, ${{x}^{n}}-{{a}^{n}}$ is exactly divisible by x-a.
$\begin{align}
& \left( {{5}^{2430}}-1={{25}^{1215}}-1,\,\,25-1\,\,\,i.e.\,\,is\,\,\,divisible\,\,by\,\,24 \right) \\
& {{5}^{2430}}-1={{\left( {{5}^{3}} \right)}^{810}}-1={{125}^{810}}-1, \\
& which\,\,\,\,is\,\,\,\,divisible\,\,by\,\,124. \\
& {{5}^{2430}}-1={{\left( {{5}^{5}} \right)}^{486}}-1, \\
& ={{\left( 3125 \right)}^{486}}-1\,\,which\,\,\,is\,\,\,divisible\,\,\,\,by\,3124. \\
\end{align}$
Question 2 |
When 1031 is divided by 999, the remainder is
1 | |
10 | |
100 | |
999 |
Question 2 Explanation:
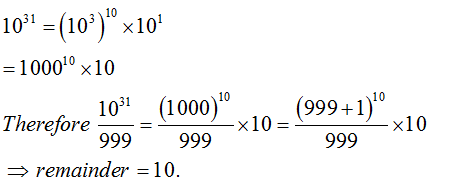
Question 3 |
Simplify: ${{\left( 0\overline{.2} \right)}^{2}}\left\{ \,3-11{{\left( 0.\overline{27} \right)}^{2}} \right\}$
$-\frac{32}{162}$ | |
$\frac{1}{297}$ | |
$\frac{76}{99}$ | |
$\frac{32}{297}$ |
Question 3 Explanation:
$\begin{align}
& {{\left( \frac{2}{9} \right)}^{2}}\left\{ 3-11{{\left( \frac{27}{99} \right)}^{2}} \right\} \\
& =\frac{4}{81}\left\{ 3-\frac{11\times 3\times 3}{11\times 11} \right\} \\
& =\frac{4}{81}\times \left\{ 3-\frac{9}{11} \right\} \\
& =\frac{4}{81}\times \left\{ \frac{24}{11} \right\} \\
& =\frac{4}{81}\times \frac{24}{11}=\frac{32}{297} \\
\end{align}$
Question 4 |
${{\left( 28 \right)}^{3}}+{{\left( 75 \right)}^{3}}-{{\left( 103 \right)}^{3}}+3\times 28\times 75\times 103$ is equal to:
10000 | |
0 | |
30007 | |
1 |
Question 4 Explanation:
$\begin{align}
& Let,\,\,28=\,\,a \\
& 75=\,b,\,-103=c \\
& When\,\,\left( a+b+c \right)=0 \\
& {{a}^{3}}+{{b}^{3}}+{{c}^{3}}-3abc=0 \\
& Here,\,\,a+b+c=\,28+75-103=0 \\
& Therefore\,\,{{(28)}^{3}}+{{\left( 75 \right)}^{3}}-{{\left( 103 \right)}^{3}}+3\times 28\times 75\times 103=0 \\
\end{align}$
Question 5 |
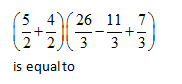
33 | |
19 | |
37 | |
36 |
Question 5 Explanation:
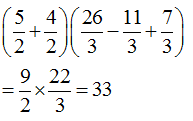
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 5 questions to complete.
List |











