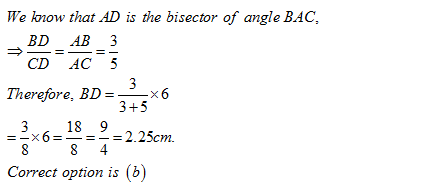- This is an assessment test.
- These tests focus on geometry and mensuration and are meant to indicate your preparation level for the subject.
- Kindly take the tests in this series with a pre-defined schedule.
Geometry and Mensuration: Test 17
Congratulations - you have completed Geometry and Mensuration: Test 17.You scored %%SCORE%% out of %%TOTAL%%.You correct answer percentage: %%PERCENTAGE%% .Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
In a triangle ABC, the lengths of the sides AB, AC and BC are 3, 5 and 6 cm respectively. If a point D on BC is drawn such that the line AD bisects the ∠A internally, then what is the length of BD?
2 cm | |
2.25 cm | |
2.5 cm | |
3 cm |
Question 2 |
If P and Q are the mid-points of the sides CA and CD respectively of a triangle ABC right angled at C. Then, the value of 4 (AQ2 + BP2) is equal to
4 BC2 | |
5 AB2 | |
2AC2 | |
2BC2 |
Question 2 Explanation:

$ \displaystyle \begin{array}{l}A{{D}^{2}}=\text{ }A{{C}^{2}}+\text{ }C{{D}^{2}}\\In\,\,PCB,\\\begin{array}{*{35}{l}} B{{P}^{2}}=\text{ }P{{C}^{2}}+\text{ }C{{B}^{2}} \\ A{{D}^{2}}+B{{P}^{2}}=\text{ }A{{C}^{2}}+C{{D}^{2}}+P{{C}^{2}}+\text{ }C{{B}^{2}} \\ =\text{ }\left( A{{C}^{2}}+C{{B}^{2}} \right)\text{ }+\text{ }\left( C{{D}^{2}}+\text{ }P{{C}^{2}} \right) \\ =\text{ }A{{B}^{2}}=\text{ }P{{D}^{2}} \\ \end{array}\\=A{{B}^{2}}{{\left( \frac{1}{2}\,AB \right)}^{2}}\\A{{D}^{2}}+\text{ }B{{P}^{2}}=\frac{4A{{B}^{2}}+A{{B}^{2}}}{4}\\Therefore\text{ }4\text{ }\left( A{{D}^{2}}+\text{ }B{{P}^{2}} \right)\text{ }=\text{ }5A{{B}^{2}}\end{array}$
Question 3 |
If the sides of a right triangle are x,x+1 and x-1,then the hypotenuse is
5 | |
4 | |
1 | |
0 |
Question 3 Explanation:
Since the triangle is a right angled triangle, We have,
(x+1)2 = x2+(x-1)2
=> x2 +2x +1 = x2 + x2-2x +1
=> x2- 4x =0
=> x(x-4) =0
=>x = 4 [x cannot be equal to 0 ]
Therefore Hypotenuse = 4+1 = 5
=> x2 +2x +1 = x2 + x2-2x +1
=> x2- 4x =0
=> x(x-4) =0
=>x = 4 [x cannot be equal to 0 ]
Therefore Hypotenuse = 4+1 = 5
Question 4 |
Let ABC be an acute-angled triangle and CD be the altitude through C. If AB = 8 and CD= 6, then the distance between the mid-points of AD and BC is
30 | |
25 | |
27 | |
5 |
Question 4 Explanation:
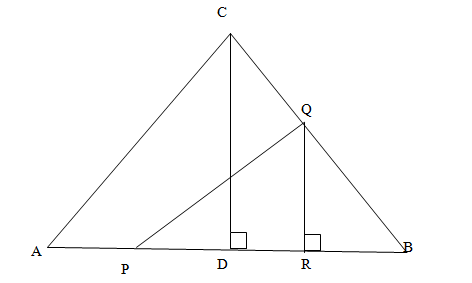
Let P and Q be the mid points of AD and BC respectively.
Draw QR perpendicular on AB. Since Q is the midpoint of BC, so R is the midpoint of BD. Hence by mid point theorem QR = 3.
Also AD = 4 = DB. So DR = PD = 2 Þ PR = 4. Hence by Pythagoras theorem, we have
PQ2 = PR2 + QR2 = 16 + 9 = 25
=>PQ = 5.
Question 5 |
4 cm | |
√6 cm | |
3 cm | |
3.5 cm |
Question 5 Explanation:
AD = CD= 6/2 = 3 cm.
BD2=ADxCD = 9.
BD= 3 cm
. Correct option is (c)
BD2=ADxCD = 9.
BD= 3 cm
. Correct option is (c)
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 5 questions to complete.
List |