Geometry and Mensuration: Test 20

This is an assessment test.
These tests focus on geometry and mensuration and are meant to indicate your preparation level for the subject.
Kindly take the tests in this series with a pre-defined schedule.

Geometry and Mensuration: Test 20

Please wait while the activity loads.
If this activity does not load, try refreshing your browser. Also, this page requires javascript. Please visit using a browser with javascript enabled.

If loading fails, click here to try again

Question 1

The side QR of an equilateral triangle PQR is produced to the point S in such a way that QR= RS and P is joined to S. Then the measure of ∠PSR is

A	30^o
B	15^o
C	60^o
D	45^o

Question 1 Explanation:

Here ∠PRQ = 60⁰ so ∠PRS = 120⁰. Now QR = PR = RS.
Hence ∠PSR = ∠RPS
Now ∠PRS + ∠PSR + ∠RPS = 180⁰
=>2 ∠PSR = 180⁰ - 120⁰ = 60⁰
=> ∠PSR = 30⁰.

Question 2

ABC is an isosceles triangle with AB= AC. A circle through B touching AC at the middle point intersects AB at P, Then AP: AB is:

A	4: 1
B	2: 3
C	3: 5
D	1: 4

Question 2 Explanation:

$\displaystyle \begin{array}{l}\begin{array}{*{35}{l}} AM\text{ }is\text{ }the\text{ }tangent\text{ }to\text{ }the\text{ }circle\text{ }and \\ APB\text{ }is\text{ }a\text{ }secant\text{ }to\text{ }the\text{ }circle. \\ So~AM{}^\text{2}\text{ }=\text{ }AP\text{ }*\text{ }AB \\ \end{array}\\\begin{array}{*{35}{l}} But\text{ }M\text{ }is\text{ }the\text{ }mid-point\text{ }of\text{ }AC\text{ }and \\ AC\text{ }=\text{ }AB \\ Thus\text{ }AM\text{ }=\text{ }\left( 1/2 \right)AB \\ \end{array}\\AM{}^\text{2}\text{ }=\text{ }\frac{1}{4}AB{}^\text{2}\\\begin{array}{*{35}{l}} and\text{ }we\text{ }have\text{ }got\text{ }AM{}^\text{2}\text{ }=\text{ }AP\text{ }\times \text{ }AB \\ Hence,\text{ }AP:AB\text{ }=\text{ }1:4 \\ \end{array}\end{array}$

Question 3

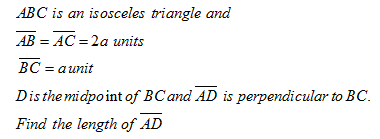
A	$\displaystyle \sqrt{15}\,\,a\,\,\,unit$
B	$\displaystyle \frac{\sqrt{15}}{2}\,\,a\,\,unit$
C	$\displaystyle \sqrt{17}\,\,a\,\,unit$
D	$\displaystyle \frac{\sqrt{17}}{2}\,\,a\,\,unit$

Question 3 Explanation:

$\begin{array}{l}\overline{AD}=\sqrt{{{(2a)}^{2}}-{{(\frac{a}{2})}^{2}}}\\=\frac{\sqrt{15}}{2}a\end{array}$

Question 4

AB⊥BC, BD⊥AC and CE bisects ∠C, ∠A= 30^o. Then what is ∠CED?

A	30^o
B	60^o
C	45^o
D	65^o

Question 4 Explanation:

$\begin{array}{l}\angle DCB={{60}^{o}}\\=>\angle DCE={{30}^{o}}\\Thus,\\\angle DEC=90-30={{60}^{o}}\end{array}$

Question 5

The sum of interior angles of a regular polygon is 720^o. The number of sides of the polygon is

A	10
B	12
C	6
D	8

Question 5 Explanation:

$\displaystyle \begin{array}{l}If\text{ }the\text{ }number\text{ }of\text{ }sides\text{ }of\text{ }regular\text{ }polygon\text{ }be\text{ }n,\text{ }then\\\left( 2n-4 \right)\times {{90}^{o}}={{720}^{o}}\\\Rightarrow 2n-4=\frac{720}{90}=8\\\Rightarrow 2n-4=8\\\Rightarrow 2n=12\\\Rightarrow n=6\end{array}$

Once you are finished, click the button below. Any items you have not completed will be marked incorrect. Get Results

There are 5 questions to complete.

List

→

Return

Shaded items are complete.