- This is an assessment test.
- These tests focus on geometry and mensuration and are meant to indicate your preparation level for the subject.
- Kindly take the tests in this series with a pre-defined schedule.
Geometry and Mensuration: Test 21
Congratulations - you have completed Geometry and Mensuration: Test 21.You scored %%SCORE%% out of %%TOTAL%%.You correct answer percentage: %%PERCENTAGE%% .Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
In the following figure, the radii of the circles with centre at 'u and 'v' is of one unit and they touch each other. These circles also touch the circle with centre at 's'. These three circles touch internally the outer circle of radius 2 units. Find the radius of the circle whose centre is 's'.


5 | |
3/2 | |
2/3 | |
None of these |
Question 1 Explanation:

$ \displaystyle \begin{array}{l}{{\left( su \right)}^{2}}={{\left( sw \right)}^{2}}+{{\left( su \right)}^{2}}\\\Rightarrow {{\left( m+1 \right)}^{2}}={{\left( rw-rs \right)}^{2}}+1\\\Rightarrow {{\left( m+1 \right)}^{2}}={{\left( 2-m \right)}^{2}}+1\\\Rightarrow {{m}^{2}}+1+2m=4+{{m}^{2}}-4m+1\\\Rightarrow 6m=4\\\Rightarrow m=\frac{2}{3}\end{array}$
Question 2 |
74o | |
106o | |
53o | |
37o |
Question 2 Explanation:
∠OBC = 37o = ∠OCB
Thus, ∠BOC = 180 -74 = 106o
∠BAC= 106/2 = 530
Correct option is (c)
Thus, ∠BOC = 180 -74 = 106o
∠BAC= 106/2 = 530
Correct option is (c)
Question 3 |
Two non-intersecting circles, one lying inside another, are of diameters a and b. The distance between their circumferences is c. The distance between their centres is
a–b–c | |
a+b–c | |
½ (a–b–c) | |
½ (a–b)–c |
Question 3 Explanation:
The distance between their centers is
= (radius of bigger circle- distance between their circumference – radius of smaller circle)
=½ a–c–½b
=½ a–½b–c
=½ (a–b)–c
Correct option is (d)
= (radius of bigger circle- distance between their circumference – radius of smaller circle)
=½ a–c–½b
=½ a–½b–c
=½ (a–b)–c
Correct option is (d)
Question 4 |
The sides of a triangle measure 4 cm, 3.4 cm and 2.2 cm. Three circles are drawn with centers at A, B and C in such a way that each circle touches the other two. Then, the diameters of these circles would measure (in cm)
1.11, 1.7, 5.0 | |
1.6, 2.8, 5.2 | |
1.5, 2.9, 5.2, | |
1.6, 3.0, 5.0 |
Question 4 Explanation:
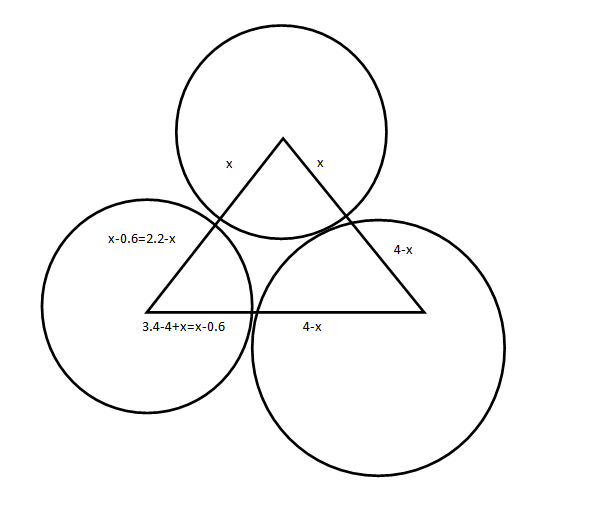
$ \displaystyle \begin{array}{l}Thus\text{ }we\text{ }can\text{ }see\text{ }that\text{ }x-0.6=2.2-x.\\=>\text{ }x=1.4\\One\text{ }of\text{ }the\text{ }diameters\text{ }is~2\times 1.4=\text{ }2.8,\\Similarly\text{ }the\text{ }others\text{ }are\text{ }1.6\text{ }and\text{ }5.2\\The\text{ }correct\text{ }option\text{ }is\text{ }\left( b \right)\end{array}$
Question 5 |
A rhombus OABC is drawn inside a circle whose center is at O in such a way that the vertices A, B and C of the rhombus are on the circle. If the area of the rhombus is 32√3 m2, then the radius of the circle is
64 m | |
8 m | |
32 m | |
46 m |
Question 5 Explanation:
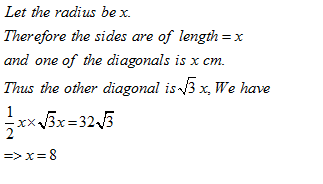
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 5 questions to complete.
List |







