- This is an assessment test.
- These tests focus on geometry and mensuration and are meant to indicate your preparation level for the subject.
- Kindly take the tests in this series with a pre-defined schedule.
Geometry and Mensuration: Test 6
Congratulations - you have completed Geometry and Mensuration: Test 6.You scored %%SCORE%% out of %%TOTAL%%.You correct answer percentage: %%PERCENTAGE%% .Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
The total area of a circle and a square is equal to 5450 sq.cm. The diameter of the circle is 70 cms. What is the sum of the circumference of the circle and the perimeter of the square?
360 cm | |
380 cm | |
270 cm | |
Cannot be determined |
Question 1 Explanation:
Radius of circle = 70/2 = 35 cm.
Area of circle = ∏r2 x 35 x 35 = 3850 m2
Area of square = 5450 – 3850 = 1600 sq. m.
length of the square = 40 m.
Required sum =2π r + 4x40 = 2 x 22/7 x 35 + 160 = 220+160 = 380 cm
Correct option is (b)
Area of circle = ∏r2 x 35 x 35 = 3850 m2
Area of square = 5450 – 3850 = 1600 sq. m.
length of the square = 40 m.
Required sum =2π r + 4x40 = 2 x 22/7 x 35 + 160 = 220+160 = 380 cm
Correct option is (b)
Question 2 |
Length of a rectangular blackboard is 8 m more than that of its breadth. If its length is increased by 7 m and its breadth is decreased by 4 m, its area remains unchanged. The length and breadth of the rectangular blackboard is
24 m, 16 m | |
20 m, 24 m | |
28 m, 20 m | |
28 m, 16 m |
Question 2 Explanation:
Let the breadth of the board is 'x' m and it s length is x + 8 m
Its area is x(x + 8).
The new length is x + 15 and new breadth is (x - 4) m.
We have
x(x + 8) = (x + 15) (x - 4)
=> x2 + 8x = x2 + 11x - 60
=> 3x = 60
=> x = 20.
Hence the length and breadth of the board are 28m and 20 m respectively.
The correct solution is (c)
Its area is x(x + 8).
The new length is x + 15 and new breadth is (x - 4) m.
We have
x(x + 8) = (x + 15) (x - 4)
=> x2 + 8x = x2 + 11x - 60
=> 3x = 60
=> x = 20.
Hence the length and breadth of the board are 28m and 20 m respectively.
The correct solution is (c)
Question 3 |
The area of a square is 1024 sq. cm. What is the respective ratio between the length and the breadth of a rectangle whose length is twice the side of the square and breadth is 12cm less than the side of the square?
5: 18 | |
16: 7 | |
14: 5 | |
None |
Question 3 Explanation:
Length of the square= √1024 =32cm
Length of the rectangle = 2x32 = 64 cm
and breadth = 32-12 = 20 cm.
Required ratio of length and breadth = 32: 20 = 8:5.
Length of the rectangle = 2x32 = 64 cm
and breadth = 32-12 = 20 cm.
Required ratio of length and breadth = 32: 20 = 8:5.
Question 4 |
A cylindrical tub of radius 12 cm contains water up to a depth of 20 cm. A spherical iron ball is dropped into the tub and thus the level of water is raised by 6.75 cm. The radius of the ball is
7.25 cm | |
6 cm | |
4.5 cm | |
9 cm |
Question 4 Explanation:
Let the radius of the ball is 'r'. We have
π ×122× (6.75) = 4/3 × π × r3
Solving we will get r= 9 cm.
π ×122× (6.75) = 4/3 × π × r3
Solving we will get r= 9 cm.
Question 5 |
A spherical ball of lead, 3 cm in diameter is melted and recast into three spherical balls. The diameter of two of these is 1.5 cm and 2 cm respectively. The diameter of the third ball is
3 cm | |
2.66 cm | |
2.5 cm | |
3.5 cm |
Question 5 Explanation:
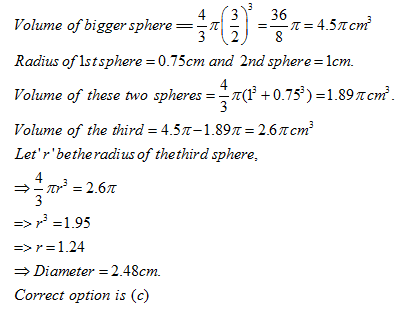
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 5 questions to complete.
List |






