We come across the term mixtures quite often. Although we understand its literal sense, but while solving problems, how do we go about it? In this article, we will study the basics of alligation and mixtures and learn various approaches to solve questions based on this topic.
Let us proceed with the basic definition first.
Mixture:
A Mixture is the result of mixing of two or more ingredients in some fixed ratio (or quantity)
Mixtures are of two types:
- Simple mixture: Simple mixture is a mixture of two ingredients like water and milk.
- Compound mixture: Compound mixture is a mixture of two simple mixtures.
Alligation:
It is a process of linking or we can say that the process of mixing the two quantities of different ingredients or different costs to form a mixture of the mean cost.
Formula derivation:
First of all, let us learn the concept of weighted average.
Example:There are two varieties of sand at Rs 20 per kg and Rs 30 per kg. They are mixed in a ratio of 1: 4. Find the average cost.
Solution: Weighted average =![]()
![]()
We can generalize the formula for weighted average.
![]()
Now let there be two ingredients that are priced at Rs x/kg and Rs y/kg.
We want to mix these ingredients in a certain ratio so that we get a price of Rs z/kg.
For that let us take m kg of the first ingredient and n kg of the second ingredient.
So, the total cost = mx + ny.
Since our required cost is Rs z/kg, we have:
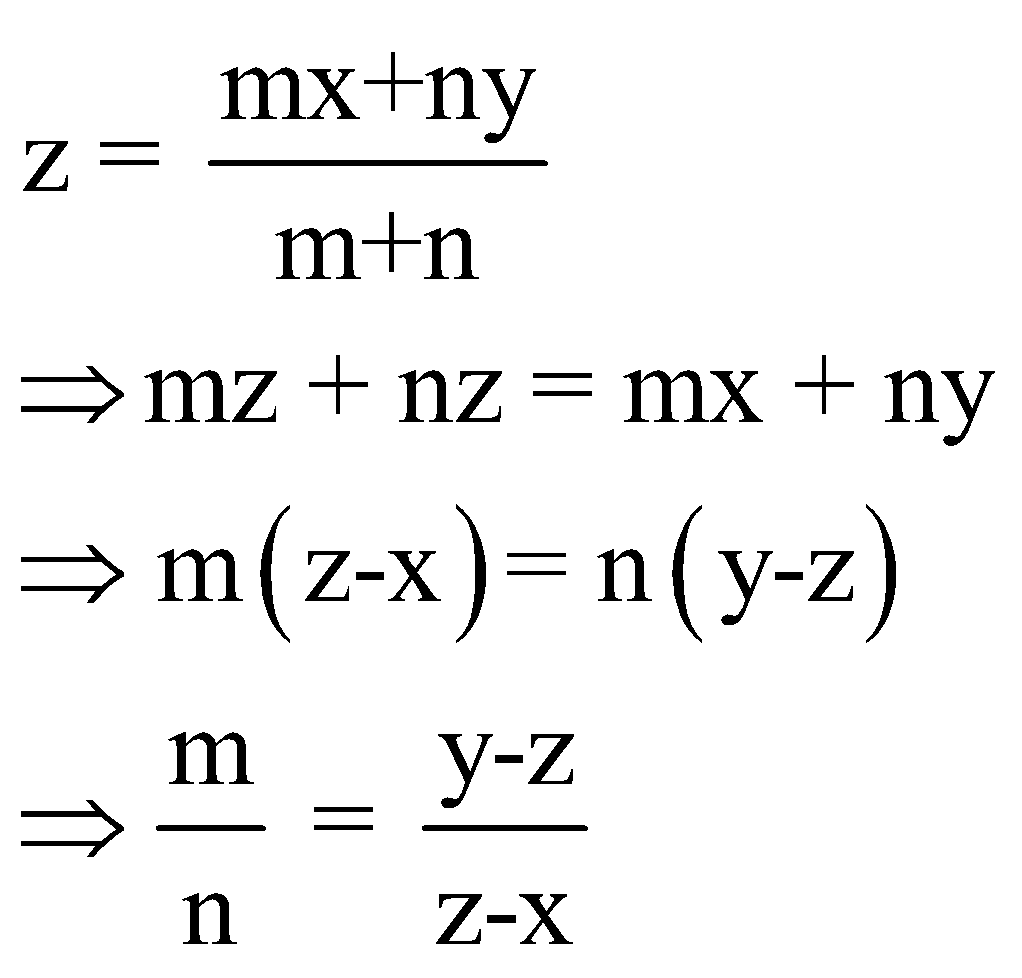
This gives us the required ratio in which the ingredients should be mixed.
Diagrammatic representation:The above relation can also be represented as follows:
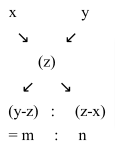
Where,
x = Price of the cheaper thing
y = Price of the dearer thing
z = Mean price
Or it can be interpreted in another way:
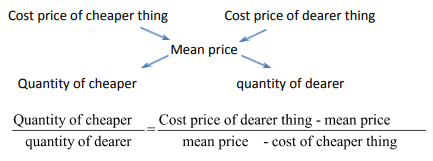
Let us now understand it with an example:
Example:In what proportionshould sand at Rs 2/kg be mixed with salt at Rs 6/kg to make a mixture of Rs 4/kg?
Solution:
Alligation Approach
Use above conceptand make the followingdiagram: (Let us assume, x=2, y=6, z=4)
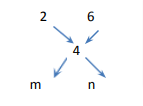
By the formula: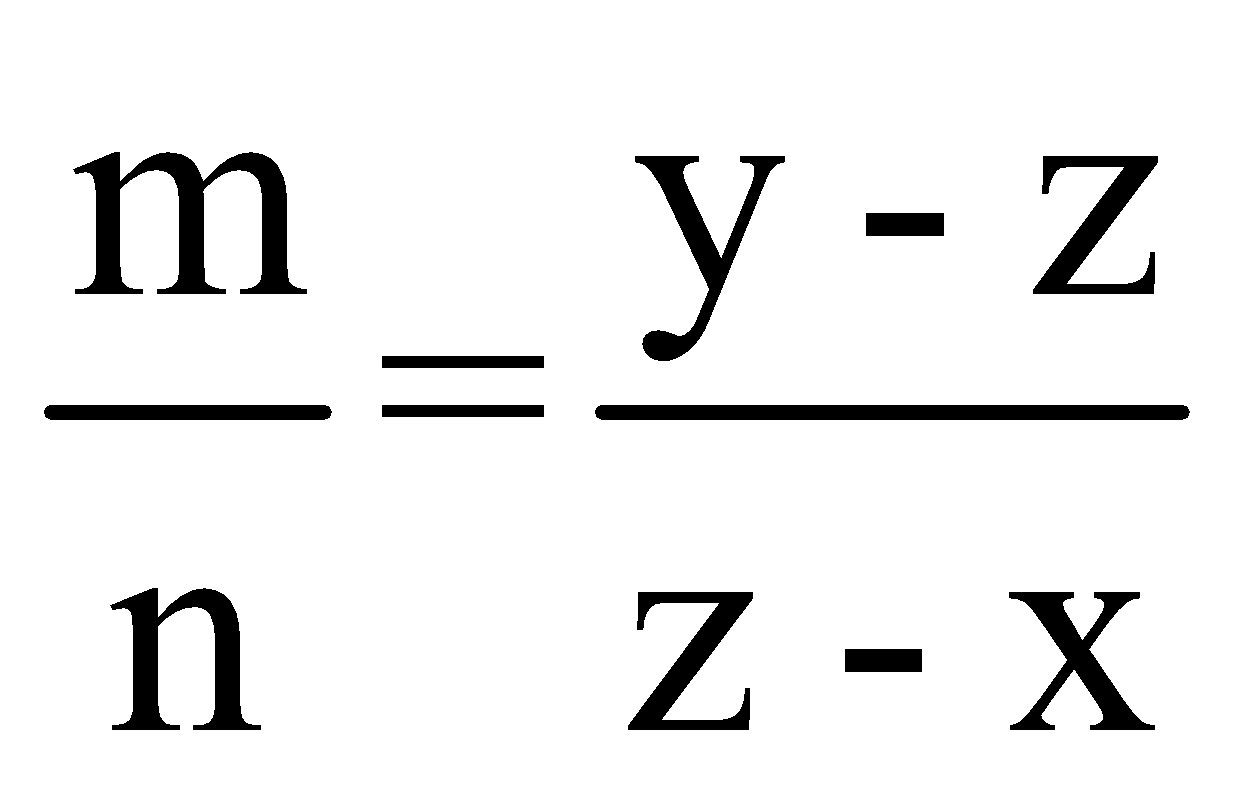
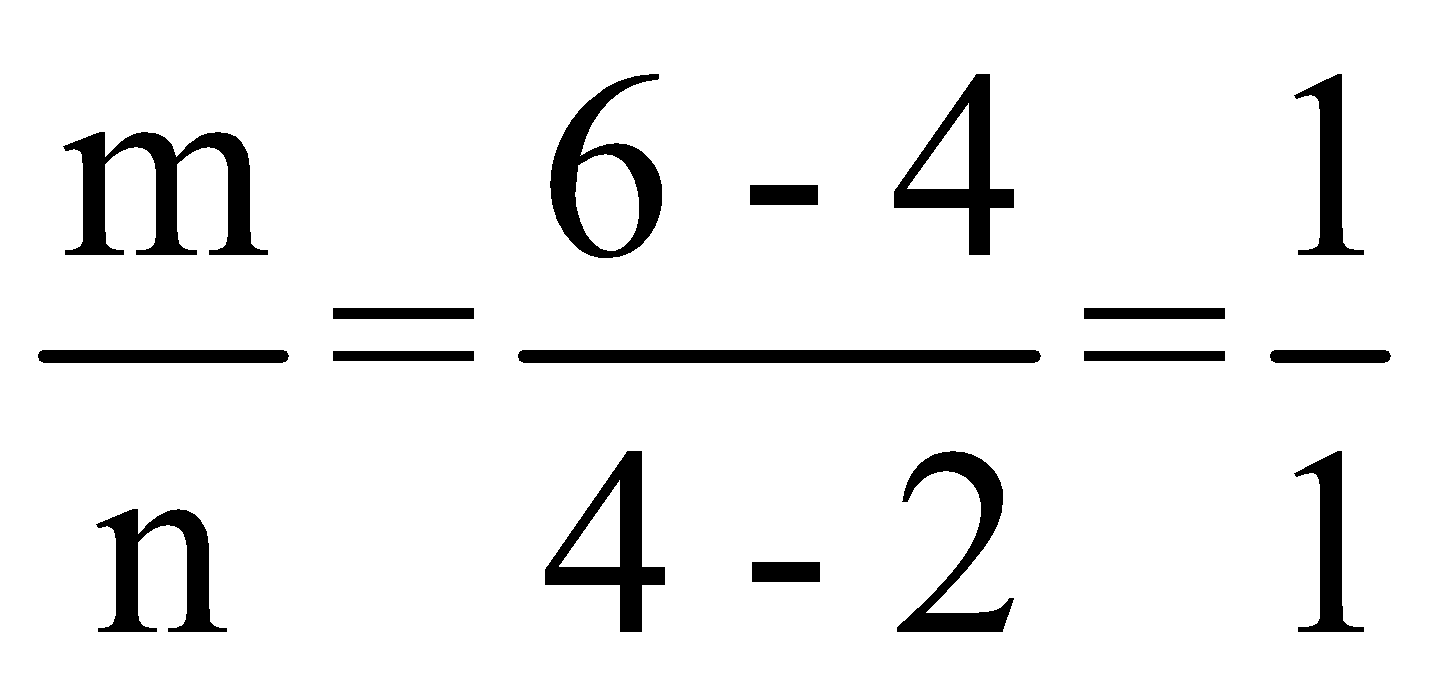
Hence the required ratio is 1: 1.
Alternate Method:
Let the required ratio be x1: x2.
Using weighted average method
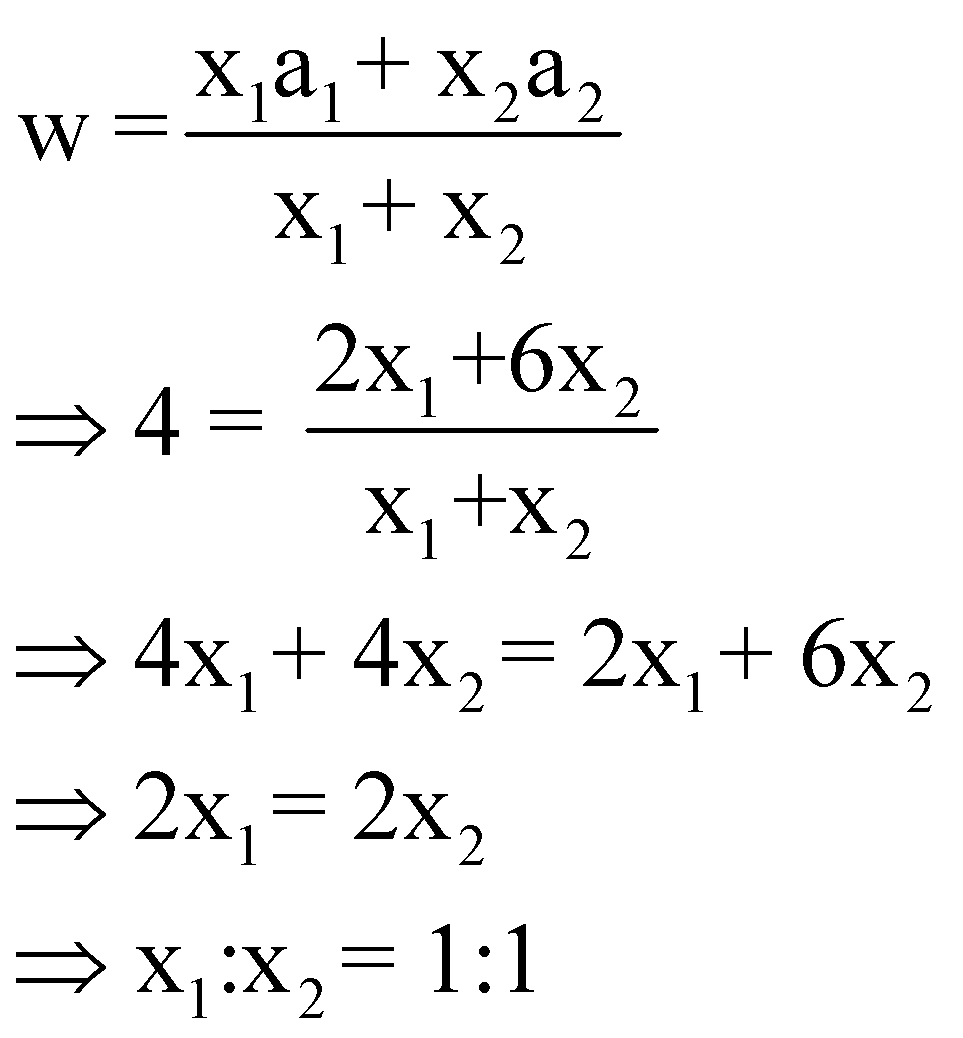
Next, we will discuss 3 types of problems generally asked from this topic:
TYPE 1:
Case of water and milk:
Whenever these types of questions occur,we need to take expenditure on water zero as no money is given for mixing water. So, the profit is all because of milk.
Let us try understanding this with the help of examples.
Example: A seller has milk at Rs 30/litre. In what ratio should water be mixed in milk so that when the seller sells the mixture at Rs 10/litre, he gets a profit of 25%.
Solution:
Let the amount milk and water mixed be ‘a’ and ‘b’respectively.
Now SP = Rs 10/litre and profit = 25%

Tip: For such type of questions, it is advisable to know the basics of profit and loss.
Alternate Method:
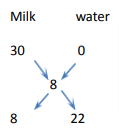
Hence the ratio will be = 8: 22 = 4:11
Example: A mixture having 20 litre water and an unknown quantity of milk is sold at Rs 50/litre. If pure milk is sold at Rs 80/litre, calculate the quantity of milk in this mixture.
Solution:
Let the quantity of milk be x litre.
So, the equation will be:
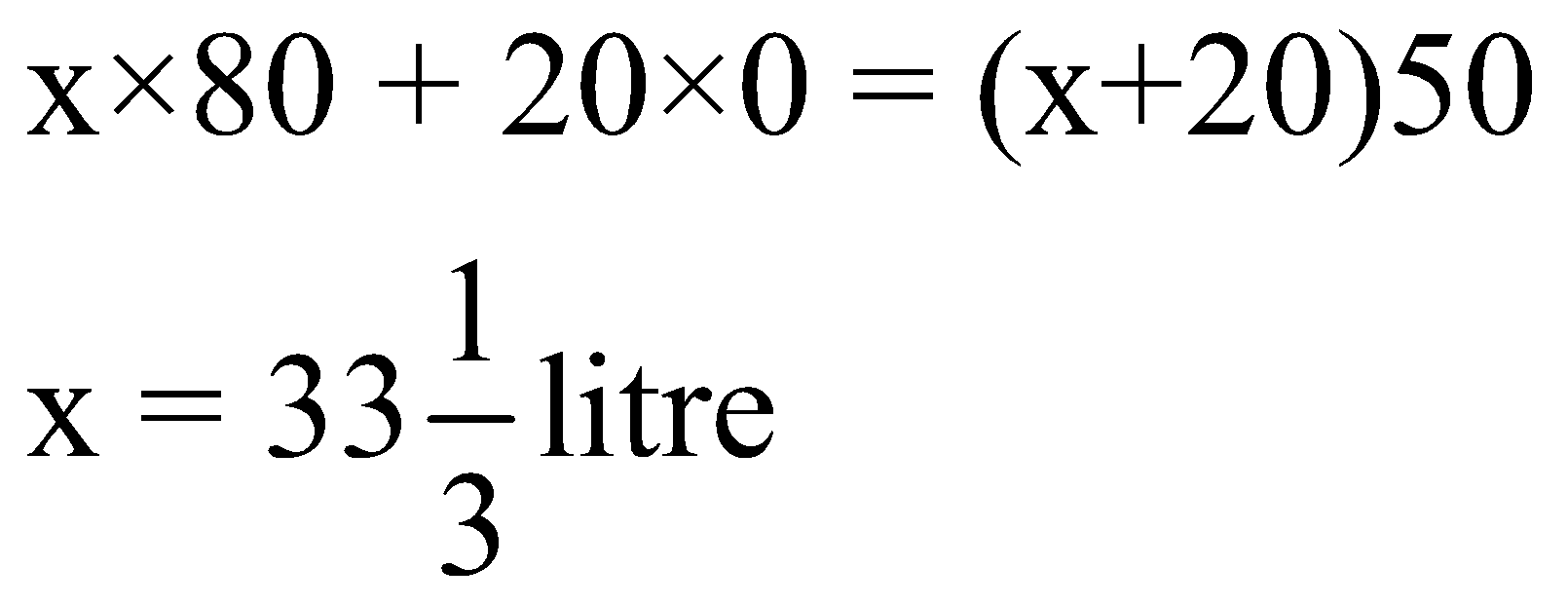
Alternate Method:
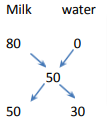
Hence the ratio of milk and water is 5: 3.
So, when the water is 3 litres, milk is 5 litres.
Then, when the water is 20 litres,milk will be =![]()
Example: In what ratio water and milk be mixed so that seller could gain 20% by selling it at cost price?
Solution:
By alligation method
Let the CP of mixture be Re 1/litre, so the SP will be Re 1 /litre.
Also Profit = 20%
So, the CP of 1 litre of milk will be:
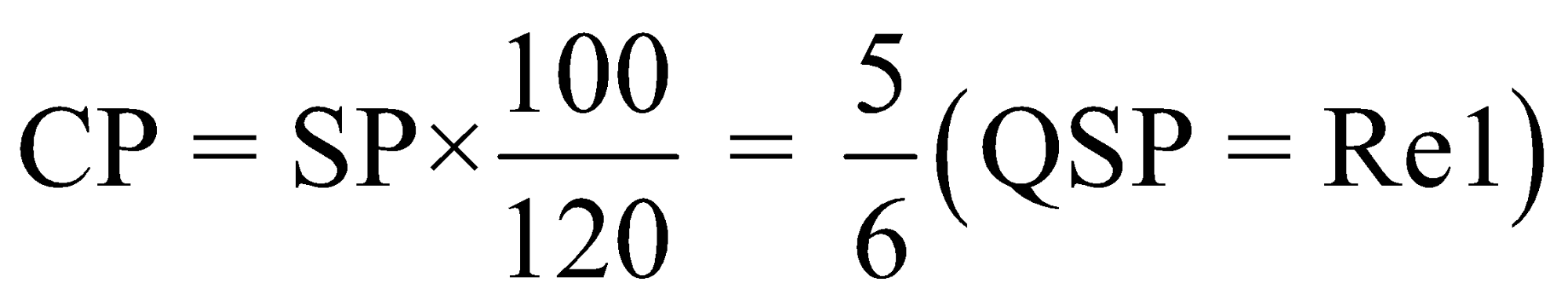
Now drawing the diagram,
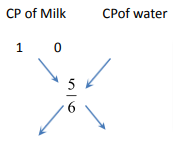
Hence the ratio of milk and water is 5: 1.
TYPE 2:
Example:A vessel contains 70 litres of a mixture of milk and water containing 90% milk.Find the quantity (in litres) of water to be added to the vessel so that the percentage of milk in the new solution is 87.5%.
Solution:
Quantity of Milk is constant after adding water(this is an important point to be kept in mind while solving the question).
In original solution, milk is ![]()
Now, after adding water let the mixture be equal to x litre. The volume of the milk is constant and is 87.5% of it.
So, we have 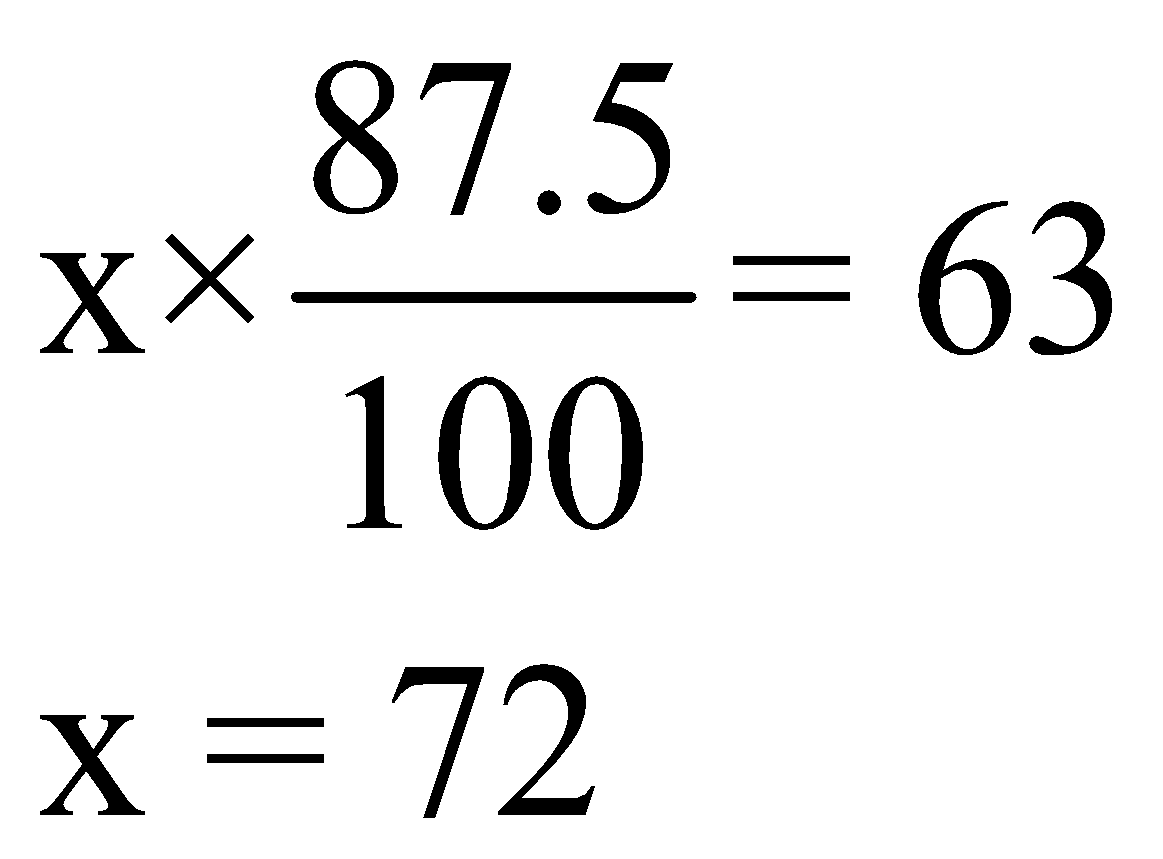
Before adding water, mixture was 70 litre and after adding water, it is 72 litres, so the water added = 72-70= 2 litre
Alternate Method:
Original solution has 10% water.
How much of water is to be added to make it 12.5%?
The solution of water that we will add has pure water that is 100% water.
So,we draw the diagram as:
Water in original solution Water to be added
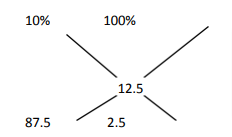
10% 100%
Ratio will be = 87.5:2.5 => 35:1
When original solution is 35 litres then water added will be 1 litre
So, when original solution is 70 litres then the water added will be ![]()
TYPE 3:
Example: A seller has 80kg sugar. A part of this is sold at 12% profit and rest is sold at 4% loss.He gets a profit of 5% on whole. What is the quantity sold at 12% gain and 4% loss?
Solution:
By allegation method
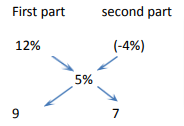
Ratio of parts will be = 9:7
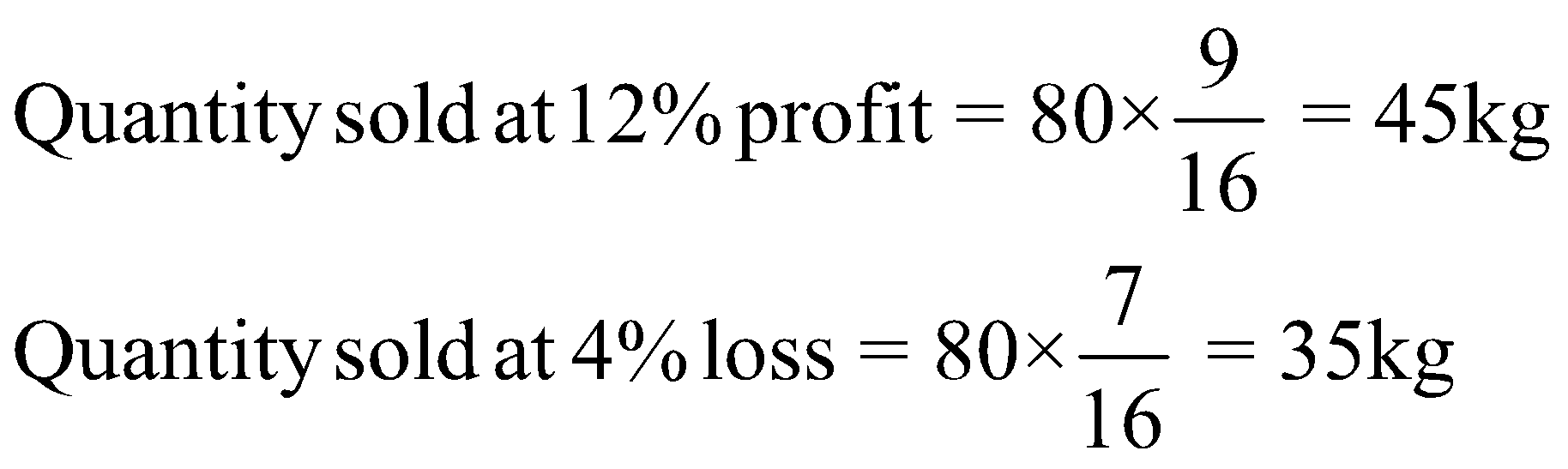
Example:A seller has 90kg sugar. A part of this is sold at 12% profit and rest is sold at 4% loss. He gets a loss of 5% on whole. What is the quantity sold at 12% gain and 4% loss?
Solution: Use allegation method directly
First part second part
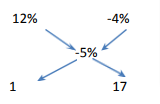
Ratio of parts will be = 1:17
We have learned various methods to solve questions on alligation and mixtures. To check which method are you comfortable with while solving questions, solve the given exercise. It will help you get a good hold on the topic.
EXERCISE:
Question 1: A mixture contains spirit and water in the ratio 3 : 2. If it contains 3 litres more spirit than water, the quantity of spirit in the mixture is
(1) 10 litres
(2) 12 litres
(3) 8 litres
(4) 9 litres
(SSC Combined Graduate LevelPrelim Exam. 11.05.2003 (Second Sitting)
Answer and Explanation
Solution: (4)
Let the amount of water be x litre. Spirit will be x+3.
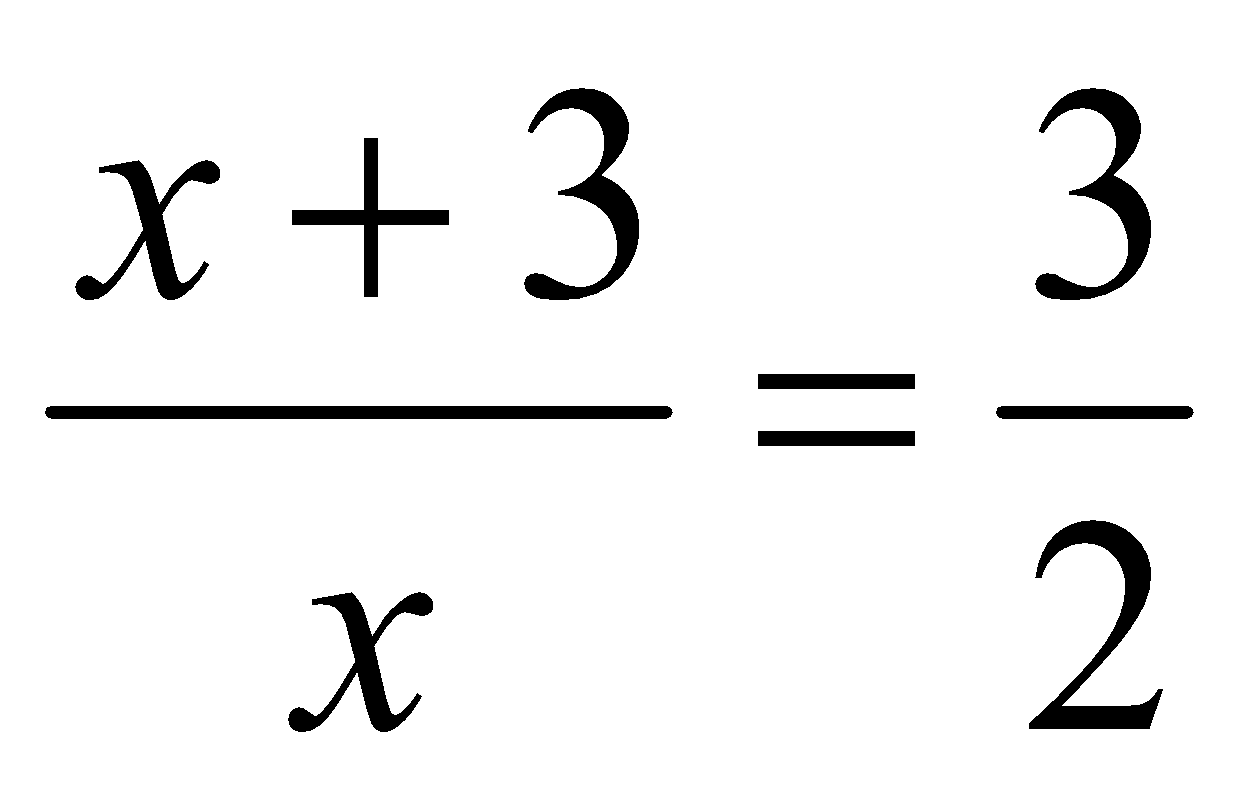
So,
Or 2x + 6 = 3x
Or x = 6
The quantity of spirit in the mixture = x + 3 = 6 + 3 = 9 litres.
Question 2: A mixture contains alcohol and water in the ratio 4 : 3. If 5 litre of water is added to the mixture, the ratio becomes 4:5. The quantity of alcohol in the given mixture is
(1) 3 litres
(2) 4 litres
(3) 15 litres
(4) 10 litres
(SSC 10+2 Data Entry Operator & LDC Exam. 27.10.2013, IInd Sitting)
Answer and Explanation
Solution: (4)
In original mixture,
Alcohol = 4x litre
Water = 3x litre
On adding 5 litre of water, new quantity of water = 3x+5
So, the ratio will be:
![]()
⇒ 20x = 12x + 20
⇒ 8x = 20
⇒ x =![]()
⇒ Quantity of alcohol= 4x = 4 × ![]() = 10 litre
= 10 litre
Question 3: In two alloys A and B, the ratio of zinc to tin is 5 : 2 and 3 : 4 respectively. 7 kgs of the alloy A and 21 kgs of the alloy B are mixed to form a new alloy. What will be the ratio of zinc and tin in the new alloy?
(1) 2 : 1
(2) 1 : 2
(3) 2 : 3
(4) 1 : 1
(SSC (10+2) Level Data Entry Operator & LDC Exam. 10.11.2013, 1st Sitting)
Answer and Explanation
Solution: (4)
In 7 kg of alloy A,
Zinc = ![]() = 5 kgs, Tin =
= 5 kgs, Tin = ![]() = 2 kgs.
= 2 kgs.
In 21 kg of alloy B
Zinc =![]() = 9 kgs,Tin =
= 9 kgs,Tin = ![]() = 12 kgs.
= 12 kgs.
Required ratio of zinc and tin in new alloy= (5 + 9) : (2 + 12)= 1 : 1
Question 4: Zinc and copper are in the ratio 5 : 3 in 400 gm of an alloy. How much of copper (in grams) should be added to make the ratio 5 : 4?
(1) 50
(2) 66
(3) 72
(4) 200
(SSC (10+2) Level Data Entry Operator & LDC Exam. 10.11.2013, IInd Sitting)
Answer and Explanation
Solution: (1)
In 400 gm of alloy,
Zinc = ![]() × 400 = 250 gm.
× 400 = 250 gm.
Copper = ![]() × 400 = 150 gm.
× 400 = 150 gm.
If x gm of copper be mixed, then new qty of copper will be 150+x.
Hence, we have
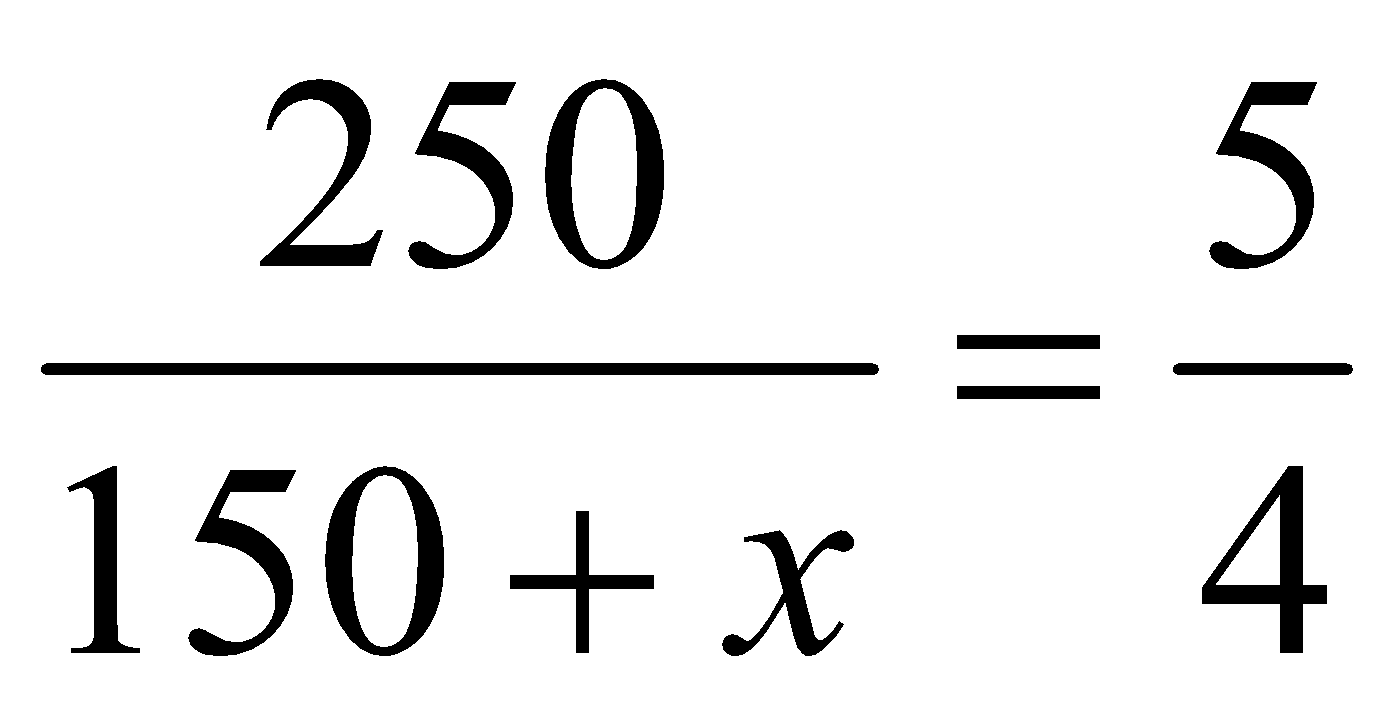
⇒ 750 + 5x = 1000
⇒ 5x = 1000 – 750 = 250
⇒ x = 50 gm.
Question 5: In an alloy there is 12% of copper. To get 69 kg of copper, how much alloy will be required?
(1)424 kg
(2) 575 kg
(3) 828 kg
(4) 1736- kg
(SSC Combined Graduate Level Prelim Exam. 24.02.2002 (Middle Zone)
Answer and Explanation
Solution: (2)
As copper is 12% of alloy
12 kg copper is contained in 100 kg of alloy.
69 kg copper is contained in=>![]() kg of alloy
kg of alloy
Question 6: How much pure alcohol must be added to 400 ml of a solution containing 15% of alcohol to change the concentration of alcohol in the mixture to 32%?
(1)60 ml
(2) 100 ml
(3) 128 ml
(4) 68 ml
(SSC Combined GraduateLevelPrelim Exam. 11.05.2003(Second Sitting)
Answer and Explanation
Solution: (2)
Alcohol = ![]() ml = 60 ml.
ml = 60 ml.
Water = 340 ml.
Let the new mixture be x ml.
Now the volume of water is constant at 340 ml, but its percentage is changed to 68%. Hence, we have

Alligations and Mixtures Questions: Problems on Alligations and Mixtures you should solve for competitive examination preparation
Welcome to this exercise on Problems on Alligations and Mixtures. In this exercise, we build on the basic concepts for Alligations and Mixtures. As you prepare for your competitive examinations, you will come across questions on Alligations and Mixtures. Such questions need optimized tackling and can be solved with ease by using simple tricks and understanding the relationships highlighted in thisAlligations and Mixtures Questions article. TheAlligations and Mixtures Questions exercise comes into the picture where it gives you a chance to practice the highlighted and important concepts related to Alligations and Mixtures question type.







