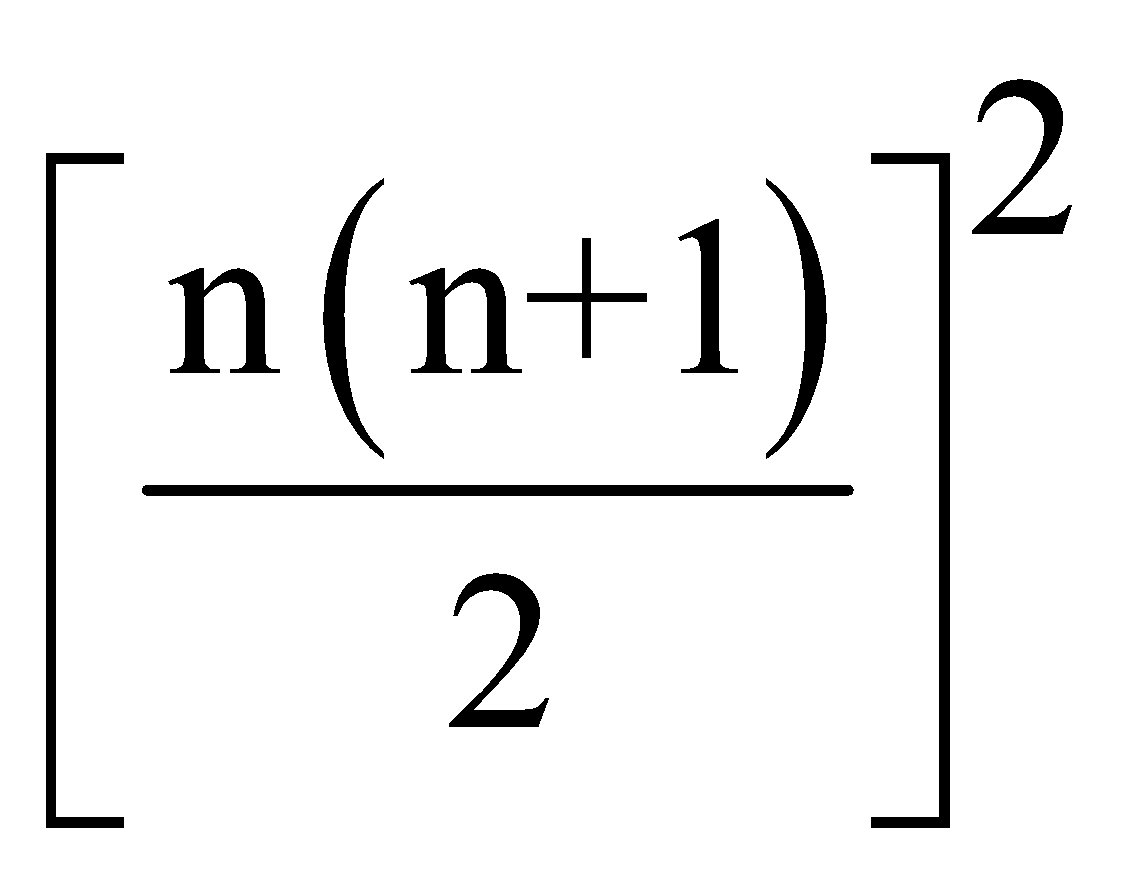CAT 2022 : Averages: Formulas, Tricks and Shortcuts

In this article, we provide you a short and effective summary for Averages. We have covered 10 formulas and shortcuts that you can use for Average questions.  The following is a list of important formulas for Averages:

1. In simple terms, averages usually refer to the sum of given numbers divided by the total number of terms listed.

Averages =

2. The Weighted Average is given by:

WeightedAverage =

Let us say, average of x numbers is A and average of y numbers is B. The sum of the first group is Ax and of second group is By.

3. If the average of n numbers is A and if we multiply p with each term then,

Then the new average will be = (A x p).

4. If the average of n numbers is A and if we divide each term by p,

Then the new average will be = (A/ p).

5. In the Arithmetic Progression, there are two cases:
   1. When the number of terms is odd, then the average will be the middle term.
   2. When number of terms is even, then the average will be the average of two middle terms.

For the terms in A.P., we can also use  to find the average of the given terms.

6. If average of n quantities is A₁.Let a new number N be added to the series and this increases the average to A₂. Then the value of new number will be:

N=n x (A₂ – A₁)+ A₂ OR N= n × (increase in value of average) + A₂

7. If average of n quantities is A₁.  Let a number is removed from the series and this decreases the average to A₂. Then the value of the number removed will be:

N= n × (A₁ – A₂) + A₂OR N= n × (decrease in value of average) + A₂

8. In some cases, a number is excluded and one more number is added in the series of the numbers, then the average will change by q and the value of the newly added term will be:

New term = Replaced Term + (increased in average × number of terms)

9. Formulae of sum of Progressions:

This can be very useful while solving problems based on Averages.

• Sum of first n natural numbers =
• Sum of first n even natural numbers =
• Sum of first n odd natural numbers =
• Sum of squares of first n natural numbers =
• Sum of cubes of first n natural numbers =
• Sum of squares of first n even natural numbers =
• Sum of squares of first n odd natural numbers
• Sum of cubes of 1^st ‘n’ Odd natural number = 1³ + 3³ + 5³ + …. + (2n -1)³ = n² (2n² -1)
• Sum of cubes of 1^st ‘n’ Even natural number = 2³ + 4³ + 6³ + …. + (2n)³ = 2 [n (n + 1)]²

10. When a number is wrongly taken while calculating the average of ‘n’ terms, then we can correct the average by the following rule:

Correct average = wrong average +

Averages Questions: Problems on averages you should solve for competitive examination preparation

Welcome to this exercise on Problems on Averages. In this exercise, we provide the summary of formulas for finding the Average. As you explore this topic, you will come across questions where you will be needing to find averages that require use of typical formulas and understanding of certain concepts. Such questions need optimized tackling and can be solved with ease by using the given formulas and understanding the relationships highlighted in this Averages Questions article. The Averages Questions exercise comes into the picture where it highlights the important concepts related to calculating the Averages and tricks you should keep in mind for this question type.