In our daily lives, we use the word ‘average’ to talk about the average speed of a car, or average marks of a class, and the average earnings of all the members of a family. The term ‘average’ shows a central value of a given set of numbers. If we dig up more in Mathematics, we can say that it shows the central tendency of those numbers. So, what does this central tendency or central value refer to?
To understand it better, let us take an example:
Example: What is the average of 12, 13, 17, 18?
Solution: Now according to the above explanation, we need to look at the central tendency or central value of the number
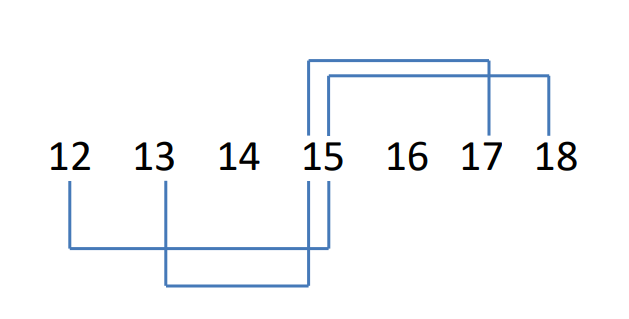
We can see from the diagram that 12 and 18 are 3 steps away from 15, while 13 and 17 are two steps away from 15. So, the central tendency of this series is 15.
An important thing to note here is “AVERAGE” is always more than the lowest number and lesser than the maximum number of that series. Now let us go deep into the topic and learn some concepts related to averages.
Concept 1
In simple terms, average usually refers to the sum of given numbers divided by the total number of terms listed.
Average = ![]()
From this we can also say that:
Sum of terms = Average × number of terms
Example: Find the average of 2, 3, 5, 4, 6.
Solution: Here, the sum of the trems = 2 + 3 + 5 + 4 + 6 = 20 and the number of terms is 5.
Average =![]()
![]()
From the explanation above, it is clear that the ‘average’ is a central value of the given of numbers. The average is also known as the arithmetic mean of the given numbers in series.
Further, an important point to note is that the average can replace each value of the given set of numbers and the sum and average will still be the same.
Confused??
Let us check this property for the above example.
Example: Find the average of 2, 3, 5, 4, 6.
Solution: We have calculated average for above series as 4.
Sum of given series = 2+3+5+4+6 =20
Now replace every number with the average, i.e., by 4.
The sum of the terms will be = 4+4+4+4+4 = 20
Again, the Average = ![]()
Concept 2
Weighted average or average of groups
Let us say, we have two groups of kids.
Let the first group has x children and their average weight is A kg.
So, the sum of their weight = Average × number of children = Ax
Let the second group has y children and their average weight is B kg.
So, the sum of their weight = Average × number of children = By
Then, the weighted Average= 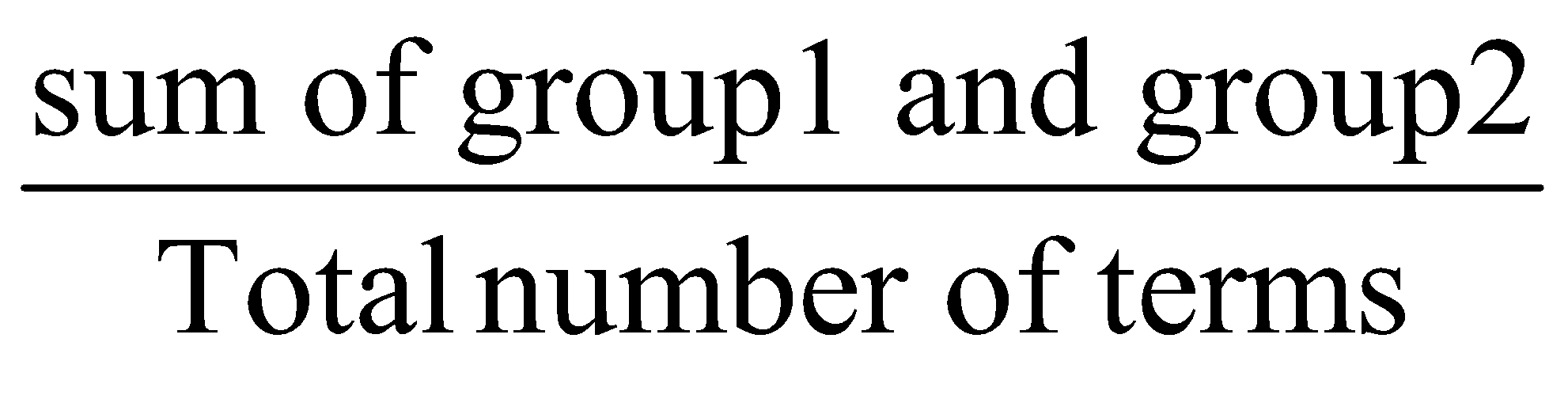
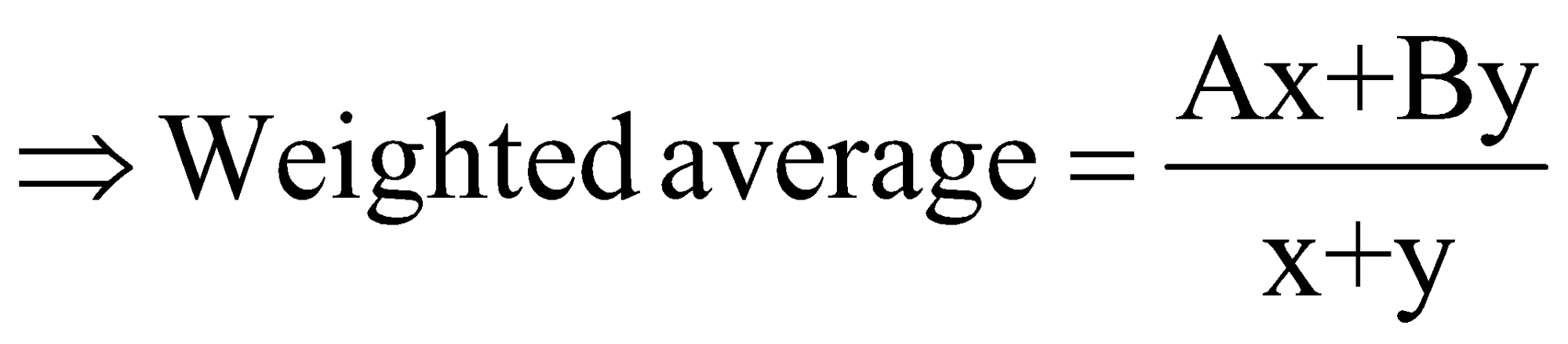
Note: This result can be extended to ‘n’ number of groups.
Example: The two varieties of sand at 20 Rs per kg and 30 Rs per kg are mixed in a ratio of 1: 4. Find the average price of sand per kg.
Solution:
Let the sand of first variety taken is 1 kg and of second variety taken is 4 kg.
Weighted average =![]()
Concept 3
If the average of n numbers is A and if we multiply p with each term, then the new average will be
= A × p.
Example: The average of 5 numbers is 18. If 4 is multiplied to each of the number, then the average would be equal to?
Solution:
Old average = 18. If 4 is multiplied to each number, the average will also be multiplied by 4.
So, the new average will be = 4 x 18= 72.
Note: The above concept will not be applicable if only some terms are multiplied by p.
Concept 4
If the average of n numbers is A and if we divide each term by p, then the new average will be =
(A/p).
Example: The average of 5 numbers is 20. If each number is divided by 2, then the average would be equal to?
Solution:
Old average = 20, when each number is divided by 2, the average will also be get divided by 2.
So, the new average will be = 20/2 = 10.
Note: The above concept will not be applicable if only some terms are divided by p.
Concept 5
If the average of n numbers is A and if we add p to each term, then the new average will be = A + p.
Example: The average of 5 numbers is 12. If 3 is added to each number, then the average would be equal to?
Solution:
The original average = 12. When 3 is added to each number, the average will increase by 3.
So, the new average = 12 + 3 = 15.
Note: The above concept will not be applicable if p is added to only some terms.
Concept 6
If the average of n numbers is A and if we subtract p from each term then the new average will be
= A – p.
Example: The average of 8 numbers is 25. If 4 is subtracted from each number, then the average would be equal to?
Solution:
The original average = 25. When 4 is subtracted from each number, the average will decrease by 4.
So, the new average = 25 – 4 = 21.
Note: The above concept will not be applicable if p is subtracted from only some terms.
Example: If the mean of 4 observations is 20, when a constant ‘C’ is added to each observation, the mean becomes 22. The value of C is:
(1) 6
(2) –2
(3) 2
(4) 4
Solution: Option 3
Here we have
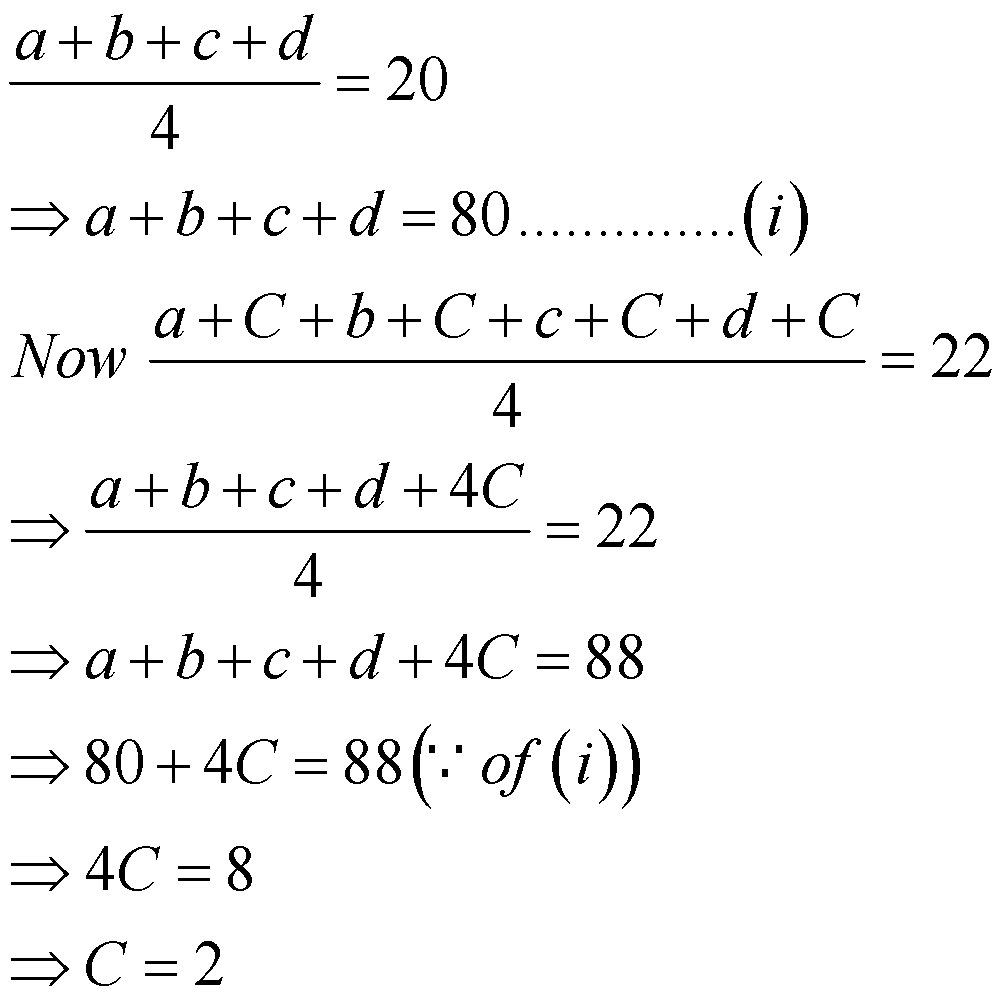
Shortcut:
In concept 5, we discussed that:
If the average of n numbers is A and if we add p to each term, then the new average will be = A + p.
Therefore, p= Difference between the two averages = 22-20 = 2.
With this, we wind up this article on the basics of averages. But before that, let’s test what we have learned by solving the below-given exercise.
EXERCISE
Question 1: Find the average of 1.11, 0.01, 0.101, 0.001, 0.11
(1) 0.2664
(2) 0.2554
(3) 0.1264
(4) 0.1164
Answer and Explanation
Answer: Option 1
According to the formula, we have Average = 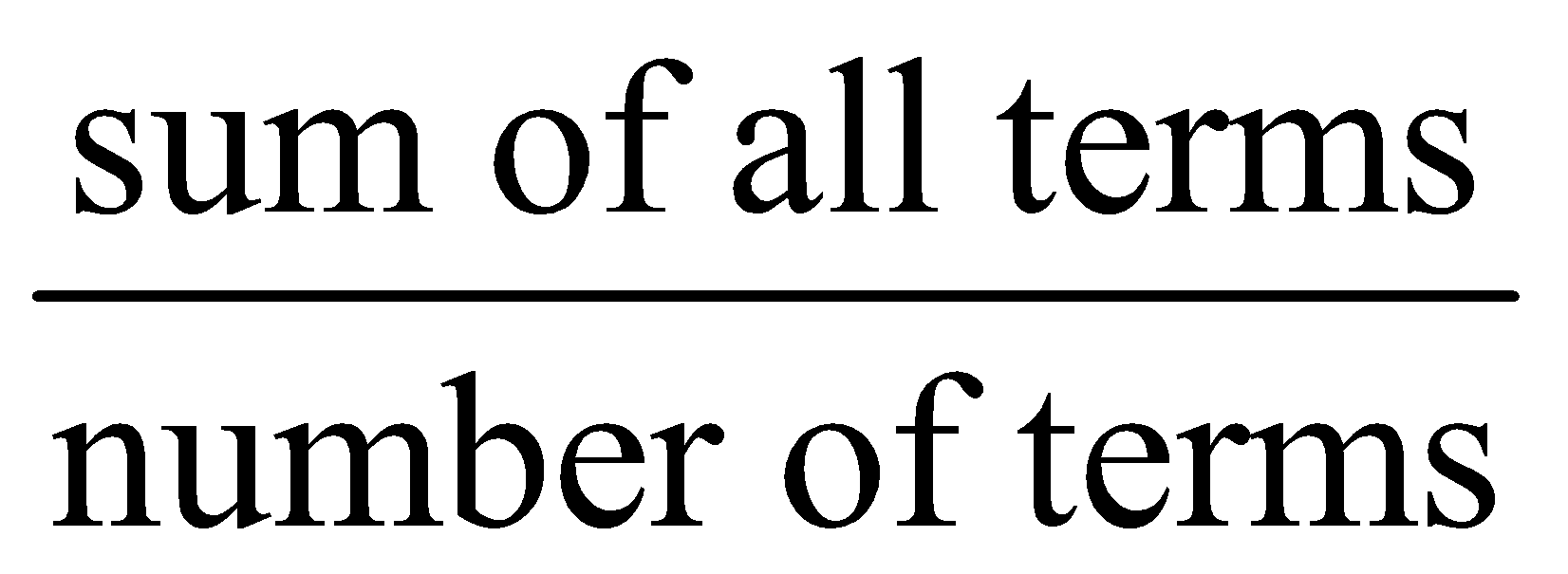
Required average 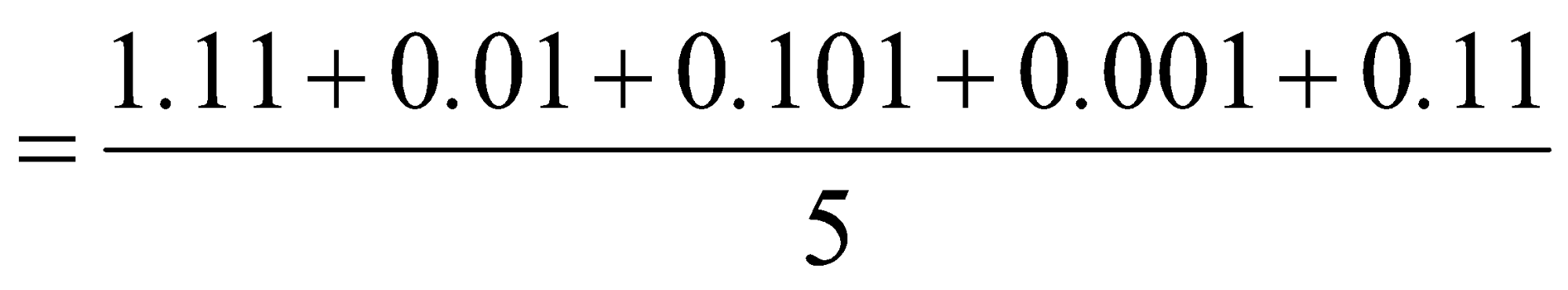
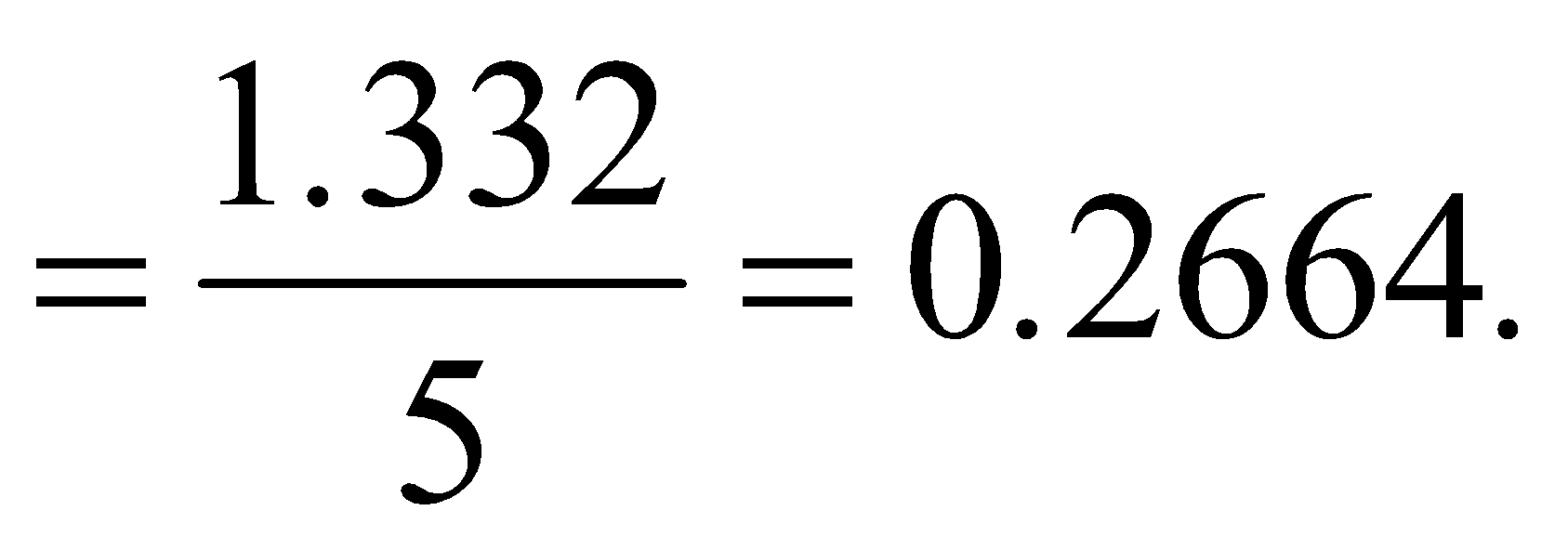
Question 2: The average of 50 numbers is 38. If two numbers namely 45 and 55 are discarded, the aver¬age of the remaining numbers is?
(1) 35
(2) 32.5
(3) 37.5
(4) 36
Answer and Explanation
We have sum of terms = average × number of terms Sum of 50 numbers will be = 50 × 38 = 1900 When 45 and 55 are discarded, the sum becomes = 1900 – 55 – 45 = 1800
Hence the required average = 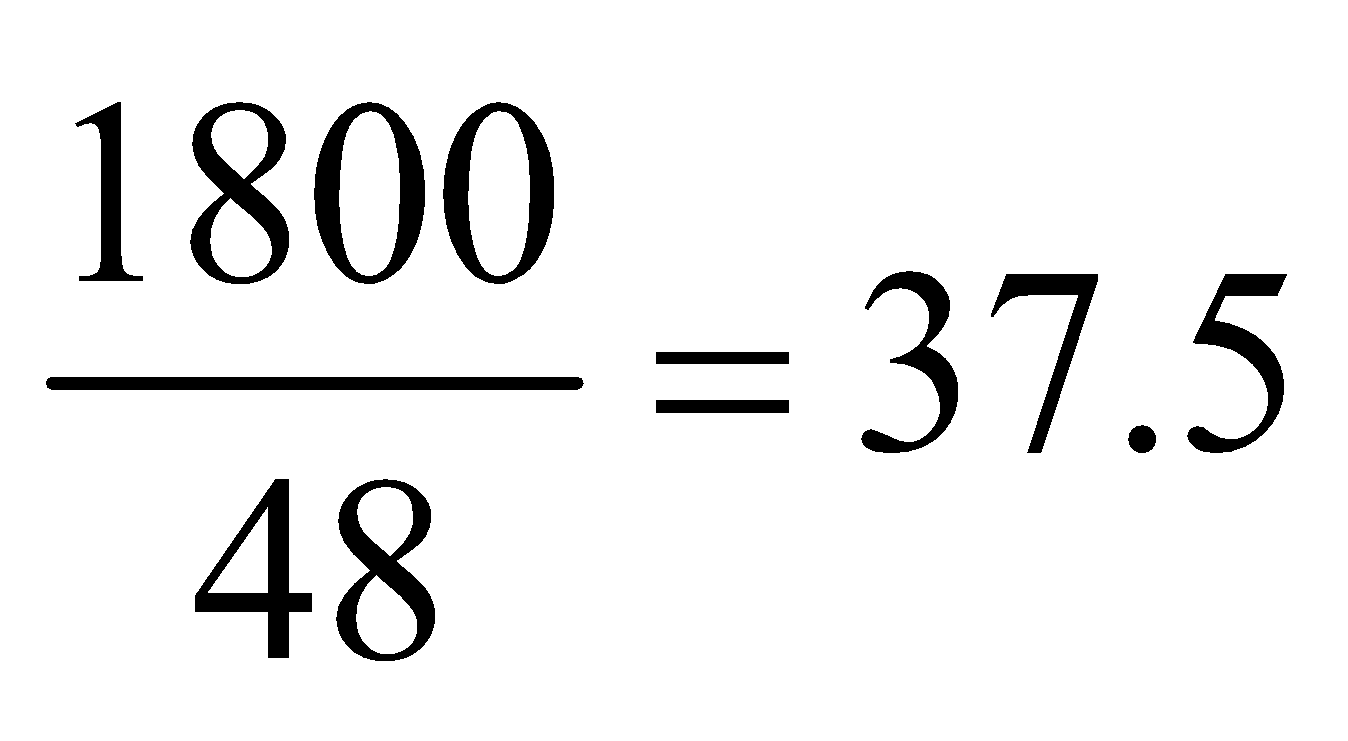
Question 3: The average of the marks obtained in an examination by 8 students was 51 and by 9 other students was 68. The average of the marks obtained by 17 students was:
(1) 59
(2) 59.5
(3) 60
(4) 60.5
Answer and Explanation
The total marks of the students = 8 × 51 + 9 × 68 = 408 + 612 = 1020
Hence, the required average = 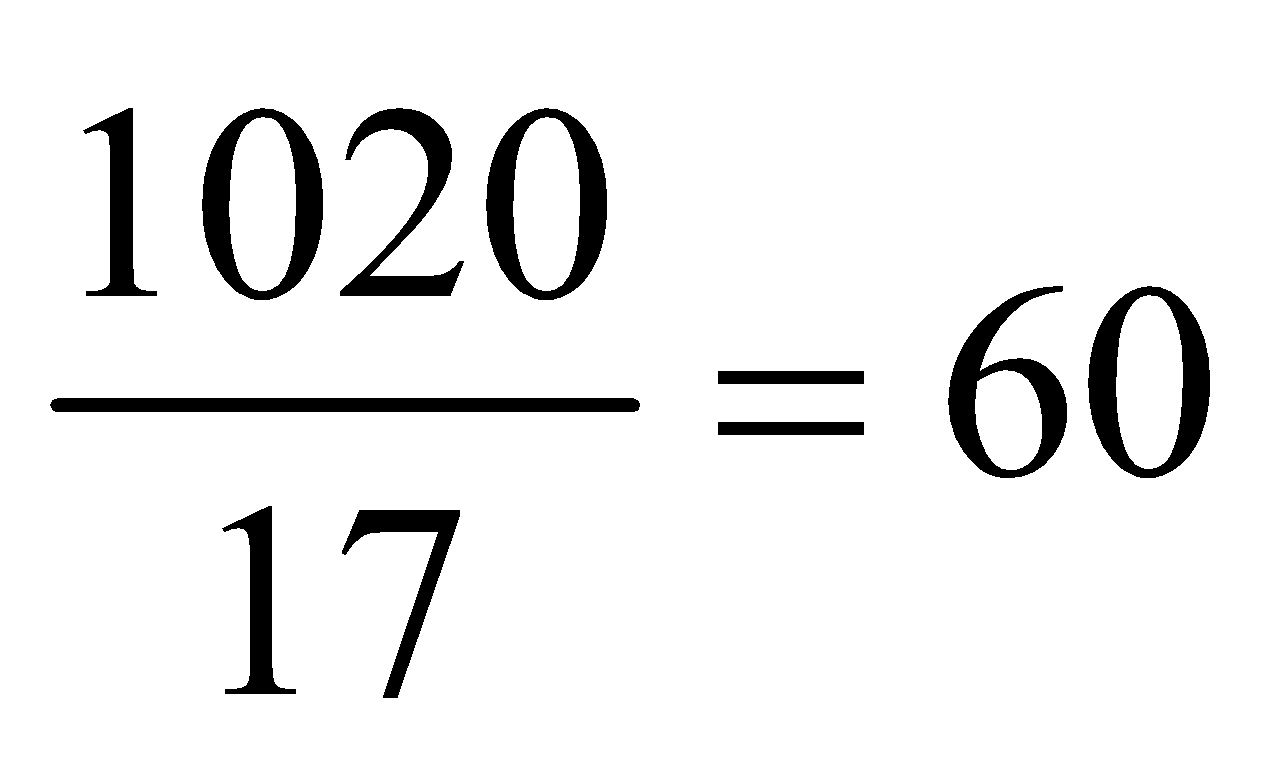
Question 4: A student was asked to find the arithmetic mean of the following 12 numbers:
3, 11, 7, 9, 15, 13, 8, 19, 17, 21, 14 and x
He found the mean to be 12. The value of x will be:
(1) 3
(2) 7
(3) 17
(4) 31
Answer and Explanation
Averages = 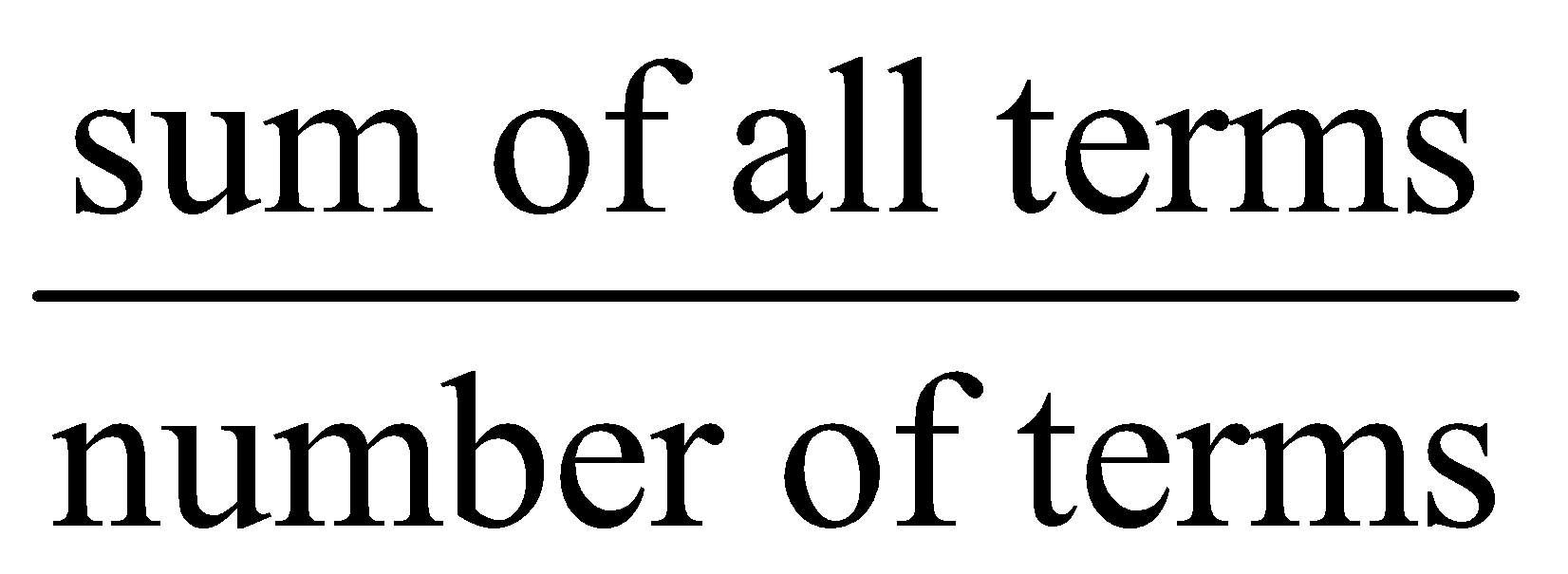
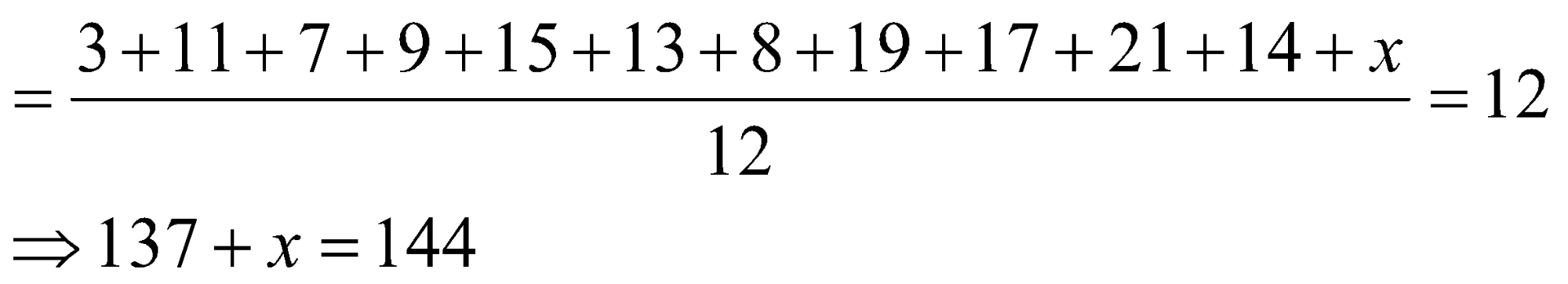
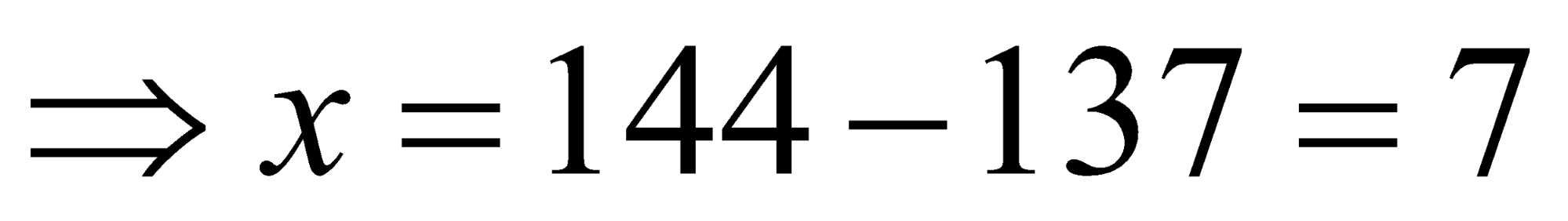
Question 5: If the average marks of three batches of 55, 60 and 45 students respectively are 50, 55 and 60, then the average marks of all the students is
(1) 54.68
(2) 53.33
(3) 55
(4) 56.46
Answer and Explanation
We have weighted average = 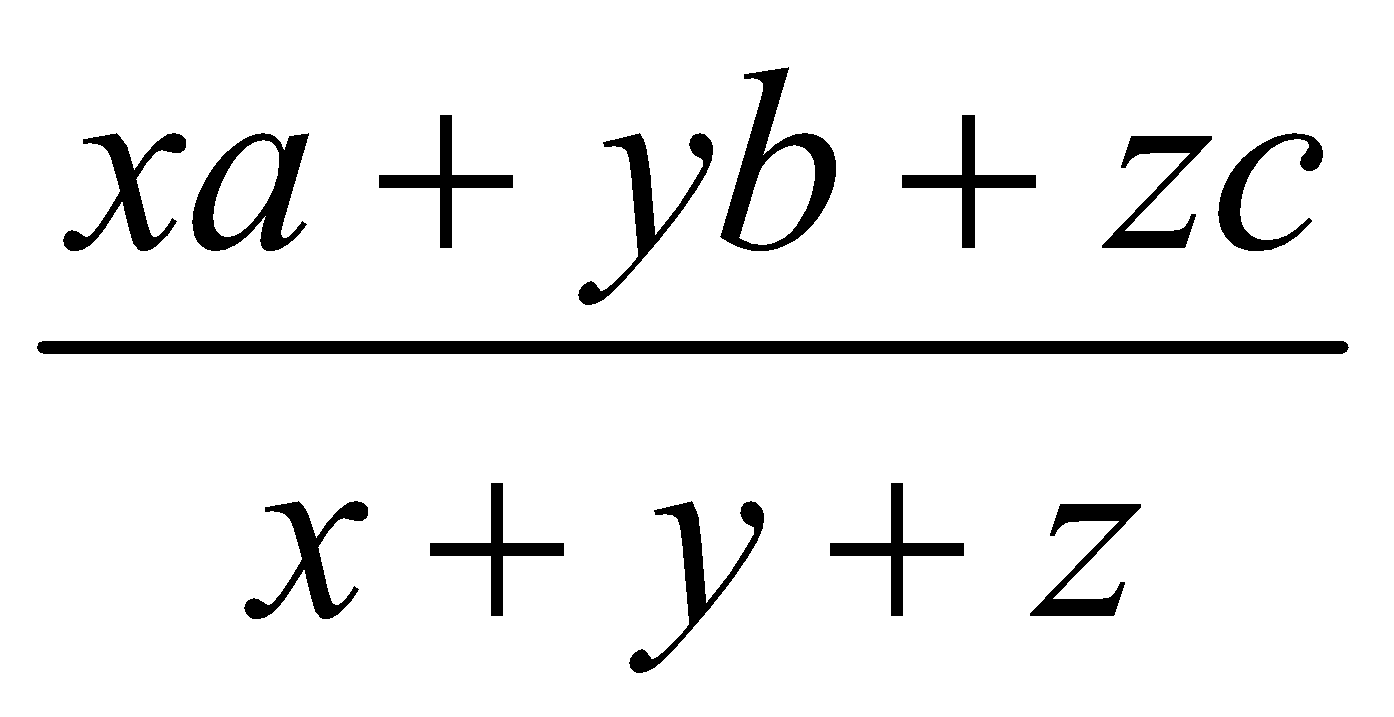
[Where x, y and z are number of students in the three batches; a, b and c are their averages respectively]
The required average marks 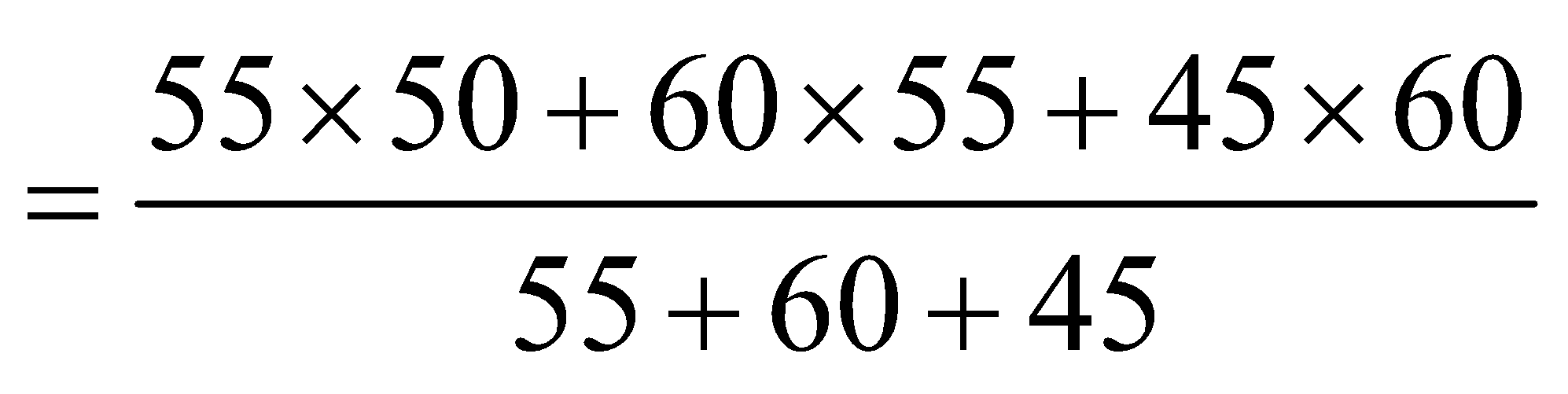
Averages Questions: Problems on averages you should solve for competitive examination preparation
Welcome to this exercise on Problems on Averages. In this exercise, we build on the basic concepts for finding the Average. As you explore this topic, you will come across questions where you will be needing to find averages. Such questions need optimized tackling and can be solved with ease by using the formulas and understanding the relationships highlighted in the Averages Questions article. This is where this simple and effective Averages Questions exercise comes into the picture: it highlights the important concepts and tricks you should keep in mind for this question type.







