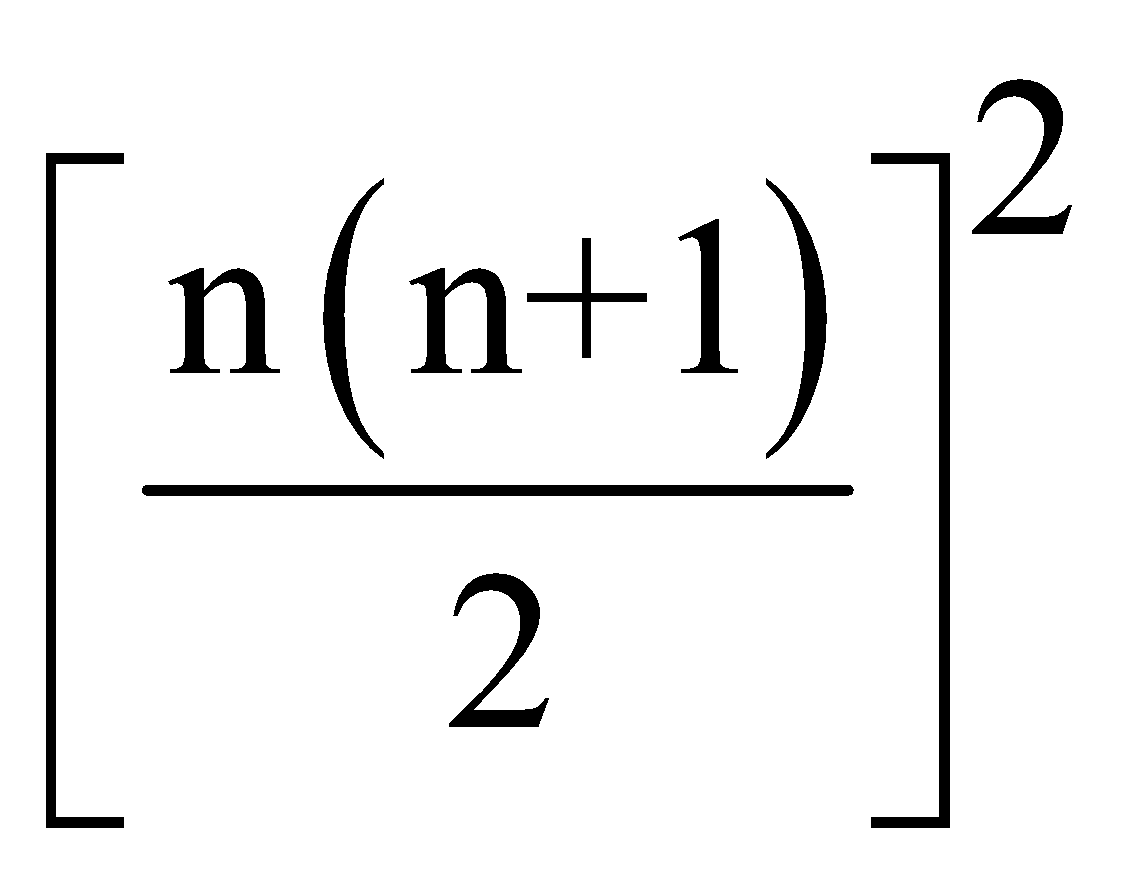Averages: Typical Concepts and Formulas - CAT 2022

As we have covered the basics of averages in the previous articles, we will now learn about some typical concepts, formulas and shortcuts that can come in handy while solving questions.

Concept 1

Let us recall some formula of arithmetic progression.

Sum of first n natural numbers =
Sum of first n even natural numbers =
Sum of first n odd natural numbers =
Sum of squares of first n natural numbers =
Sum of cubes of first n natural numbers =
Sum of squares of first n even natural numbers =
Sum of squares of first n odd natural numbers=
Sum of cubes of 1^st‘n’ Odd natural number = 1³+ 3³+ 5³ + …. + (2n -1)³ = n² (2n² -1)
Sum of cubes of 1^st ‘n’ Even natural number = 2³ + 4³ + 6³ + …. + (2n)³= 2 [n (n + 1)]²

Note: These formulas have wide applications in the Quant and DILR section of all competitive exams. Therefore, it is advisable that you learn them by heart.

Given below are some questions based on the above-discussed formulas.

Question 1: Find the average of first 20 odd numbers.

(1) 20

(2) 18

(3) 16

(4) 14

Answer and Explanation

Solution:Option 1

Sum of first n odd numbers =

Average =

So, average = 20.

Question 2: Find the average of first 30 even numbers.

(1) 30

(2) 31

(3) 36

(4) 34

Answer and Explanation

Solution: Option 2

Sum of first n even numbers =

Average =

So, the average will be 30+1 = 31

Question 3: Find average of odd numbers from 1 to 29.

(1) 20

(2) 15

(3) 16

(4) 14

Answer and Explanation

Solution: Option 2

There are 15 odd numbers from 1 to 29 and their sum is 15².

Hence their average =

Question 4: Find average of even numbers from 1 to 30.

(1) 15

(2) 16

(3) 17

(4)18

Answer and Explanation

Solution:Option 2

There are 15 even numbers from 1 to 30 and their sum is n(n+1)= 15 × 16.

Hence the average =

Concept 2

When a number is wrongly taken while solving average.

If average of n quantities is A₁. It was later discovered that while calculating average, one number ‘a’ was wrongly read as a₁, so the correct average will be:

Correct average = wrong average +

Derivation:

Let the wrong average = A₁and wrongly read number = a₁

Let The correct average = A₂and the correct number = a

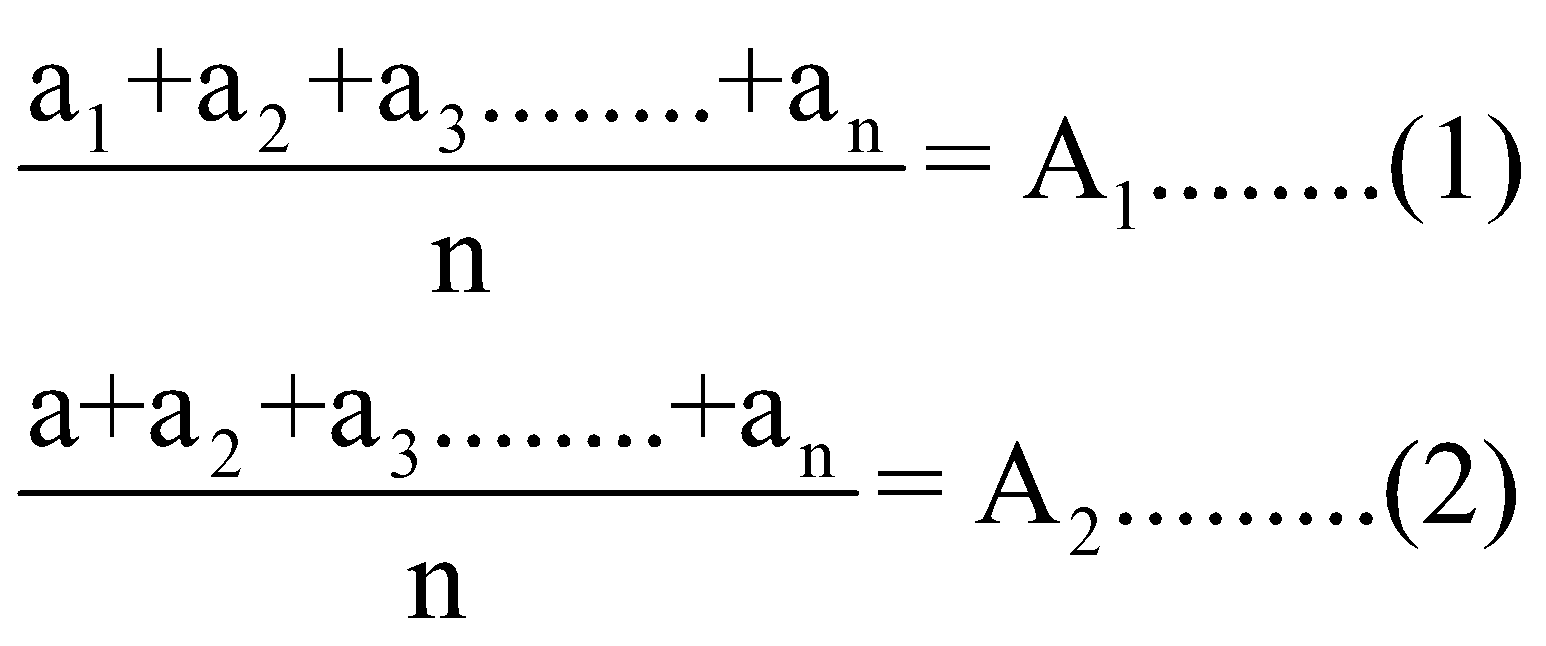
Subtracting (2) from (1), we get:

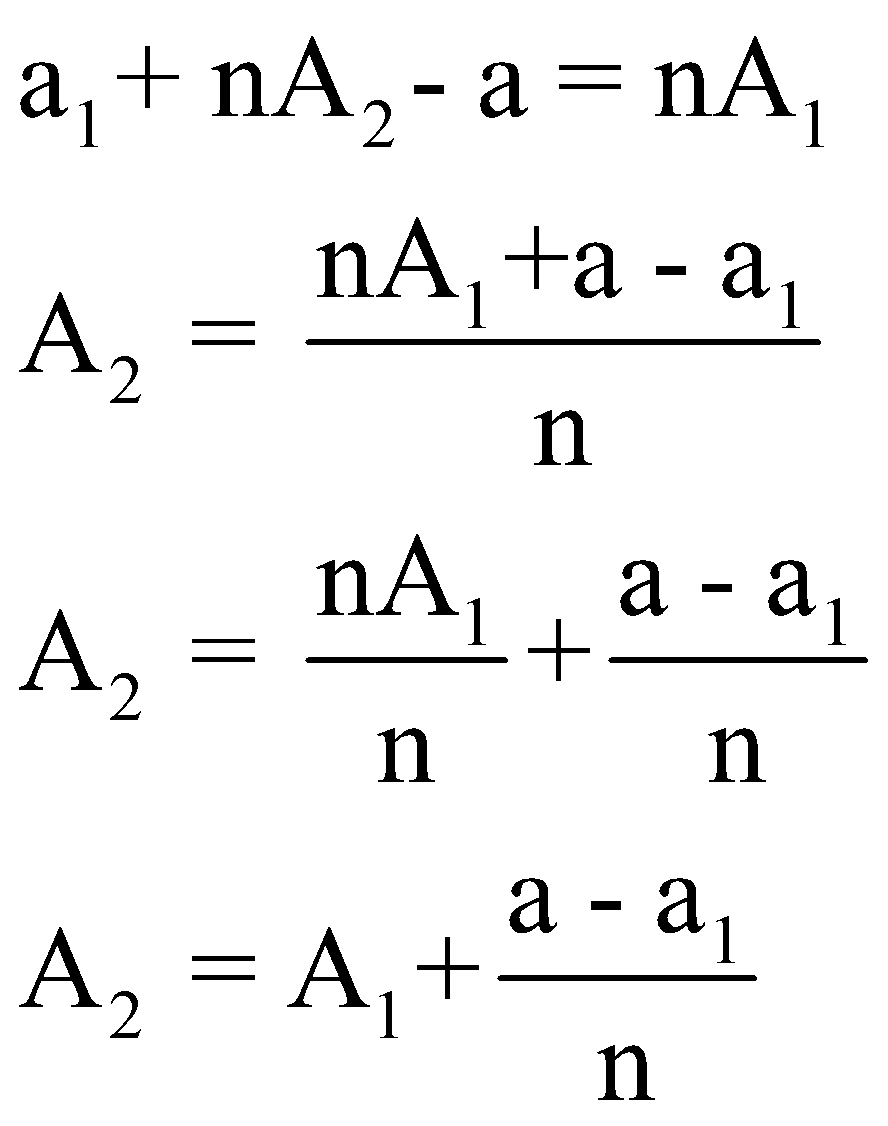
Correct average = wrong average +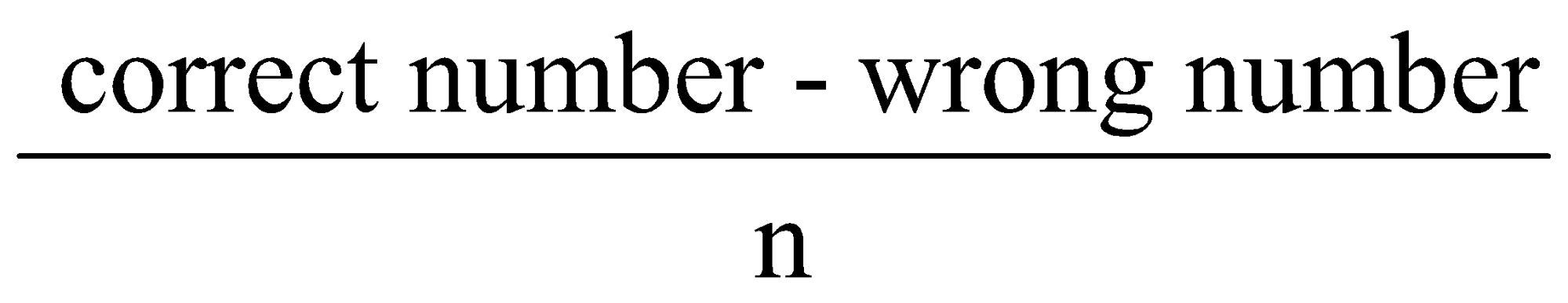

Question 5: The average of 10 numbers is calculated as 15. It is later discovered that while calculating the average, one numbernamely 36, was wrongly read as 26. The correct average is?

(1) 20

(2) 18

(3) 16

(4) 14

Answer and Explanation

Solution: Option 3

We have the Sum of terms = Average × number of terms

Sum of the numbers = 15 × 10=150

Now the difference between 36 and 26 = 10

So new sum = 150+10=160

New average =

Or we can directly use the formula:

Correct average = wrong average +

Concept 3

When one or more than one, new items are added, then we can calculate average of newly added items as follows:

Let the average of original N items be = original average

So,the Average of new items added = original average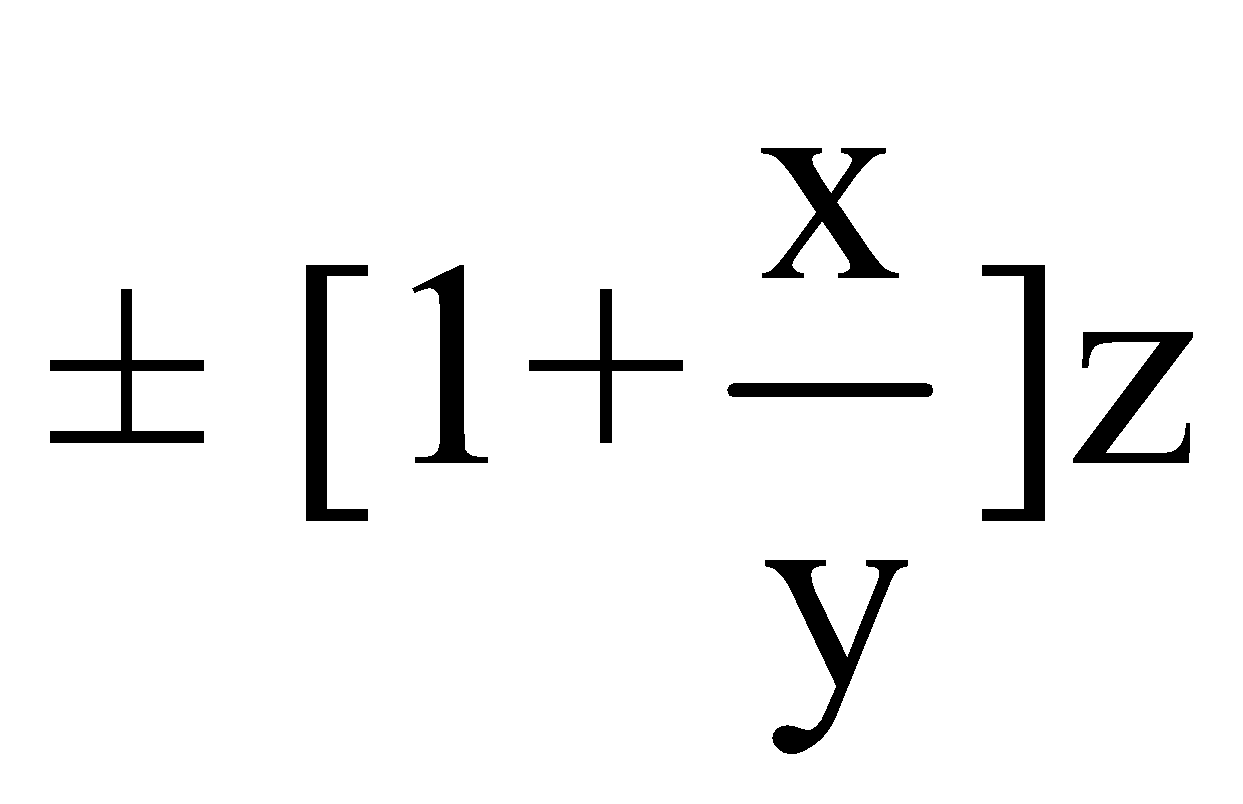

Where x is the original numbers, y is the numbers added and z is the change in average.

Use plus sign if average is increased and use minus sign if average is decreased.

Question 6: Average of 60 students is 20 years. When 10 new students are added,average increased by 0.5years. Find the average age of new students.

Answer and Explanation

Solution:

Average of new items added = original average

(Where x is the original numbers, y is the numbers added and z is the change in average.)

Averages Questions: Problems on averages you should solve for competitive examination preparation

Welcome to this exercise on Problems on Averages. In this exercise, we build on the basic concepts for finding the Average. As you explore this topic, you will come across questions where you will be needing to find averages that require use of typical formulas. Such questions need optimized tackling and can be solved with ease by using the given formulas and understanding the relationships highlighted in this Averages Questions article. The Averages Questions exercise comes into the picture where it highlights the important concepts related to calculating the Averages and tricks you should keep in mind for this question type.