- This is an assessment test.
- These tests focus on the basics of Maths and are meant to indicate your preparation level for the subject.
- Kindly take the tests in this series with a pre-defined schedule.
Basic Maths: Test 46
Congratulations - you have completed Basic Maths: Test 46.
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
$\left[ \frac{{{\left( 0.54 \right)}^{3}}+{{\left( 0.45 \right)}^{3}}}{{{\left( 0.54 \right)}^{2}}+{{\left( 0.45 \right)}^{2}}-\left( 0.54 \right)\times \left( 0.45 \right)} \right]$
Simplifies to:
1 | |
0.4087 | |
0.73 | |
0.27 |
Question 1 Explanation:
Let 0.54= a and 0.45 = b
Therefore expression
$\begin{align} & =\frac{{{a}^{3}}+{{b}^{3}}}{{{a}^{2}}+{{b}^{2}}-ab} \\ & =\frac{\left( a+b \right)\left( {{a}^{2}}+{{b}^{2}}-ab \right)}{{{a}^{2}}+{{b}^{2}}-ab} \\ & =a+b=0.54+0.45=1 \\ \end{align}$
Therefore expression
$\begin{align} & =\frac{{{a}^{3}}+{{b}^{3}}}{{{a}^{2}}+{{b}^{2}}-ab} \\ & =\frac{\left( a+b \right)\left( {{a}^{2}}+{{b}^{2}}-ab \right)}{{{a}^{2}}+{{b}^{2}}-ab} \\ & =a+b=0.54+0.45=1 \\ \end{align}$
Question 2 |
$\left( 79\times 21+25\times 17+7\times 3 \right)$
equals
2450 | |
2405 | |
2150 | |
2105 |
Question 2 Explanation:
Expression
$\begin{align} & =\left( 79\times 21+25\times 17+7\times 3 \right) \\ & =1659+425+21=2105 \\ \end{align}$
$\begin{align} & =\left( 79\times 21+25\times 17+7\times 3 \right) \\ & =1659+425+21=2105 \\ \end{align}$
Question 3 |
$\left( 0.06\times 6-0.006\times 6 \right)$ is equal to:
3.240 | |
0.366 | |
0.324 | |
0.342 |
Question 3 Explanation:
Expression
$\begin{align} & =0.06\times 6-0.006\times 6 \\ & =0.36-0.036=0.324 \\ \end{align}$
$\begin{align} & =0.06\times 6-0.006\times 6 \\ & =0.36-0.036=0.324 \\ \end{align}$
Question 4 |
The value of
$\sqrt[3]{\frac{0.3\times 0.3\times 0.3+0.05\times 0.05\times 0.05}{0.6\times 0.6\times 0.6+0.1\times 0.1\times 0.1}}$
is
0.5 | |
0.25 | |
0.75 | |
0.125 |
Question 4 Explanation:
Let 0.3= a and 0.05= b
Therefore 0.6 = 2a and 0.1 = 2b
Therefore expression

Therefore 0.6 = 2a and 0.1 = 2b
Therefore expression
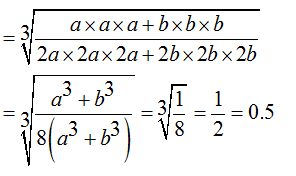
Question 5 |
$\frac{{{\left( 2.25 \right)}^{\frac{1}{2}}}\times {{\left( 0.0196 \right)}^{\frac{1}{2}}}+1-0.01}{{{\left( 0.064 \right)}^{\frac{1}{3}}}\times {{\left( 16 \right)}^{\frac{1}{4}}}}$
is simplified to
0.15 | |
1.5 | |
1 | |
$1.\overline{5}$ |
Question 5 Explanation:
Expression
$\begin{align} & =\frac{{{\left( 2.25 \right)}^{\frac{1}{2}}}\times {{\left( 0.0196 \right)}^{\frac{1}{2}}}+1-0.01}{{{\left( 0.064 \right)}^{\frac{1}{3}}}\times {{\left( 16 \right)}^{\frac{1}{4}}}} \\ & =\frac{{{\left( 1.5 \right)}^{2\times \frac{1}{2}}}\times {{\left( 0.14 \right)}^{2\times \frac{1}{2}}}+1-0.01}{{{\left( 0.4 \right)}^{3\times \frac{1}{3}}}\times {{\left( 2 \right)}^{4\times \frac{1}{4}}}} \\ & =\frac{1.5\times 0.14+1-0.01}{0.4\times 2}=\frac{0.21+1-0.01}{0.8} \\ & =\frac{1.20}{0.8}=\frac{120}{80} \\ & =1.5 \\ \end{align}$
$\begin{align} & =\frac{{{\left( 2.25 \right)}^{\frac{1}{2}}}\times {{\left( 0.0196 \right)}^{\frac{1}{2}}}+1-0.01}{{{\left( 0.064 \right)}^{\frac{1}{3}}}\times {{\left( 16 \right)}^{\frac{1}{4}}}} \\ & =\frac{{{\left( 1.5 \right)}^{2\times \frac{1}{2}}}\times {{\left( 0.14 \right)}^{2\times \frac{1}{2}}}+1-0.01}{{{\left( 0.4 \right)}^{3\times \frac{1}{3}}}\times {{\left( 2 \right)}^{4\times \frac{1}{4}}}} \\ & =\frac{1.5\times 0.14+1-0.01}{0.4\times 2}=\frac{0.21+1-0.01}{0.8} \\ & =\frac{1.20}{0.8}=\frac{120}{80} \\ & =1.5 \\ \end{align}$
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 5 questions to complete.
List |






