In this article we would be going through the important concept of boats and streams. It is based on the concept of relative speed, which was covered in the previous article. Whenever a boat moves in the direction of the stream, it is said to be moving downstream whereas when it moves in the direction opposite to that of the stream, it is said to be moving upstream.
Likewise, the speed of the boat when it moves downstream is called downstream speed and the speed of the boat when it moves upstream is called the upstream speed.
Formulation:
Let the speed of the boat in still water is ‘x’ km/hr and the speed of the stream is ‘y’ km/hr. When the boat goes downstream, then the water will help the boat by pushing it forward. So, in this case the net speed of the boat will become x + y km/hr. On the other hand, when the boat moves upstream then the water works against it and offers it resistance. So, the net speed is x – y km/hr.
Let the downstream speed is ‘d’ and the upstream speed is ‘u’. So, we have
d = x + y ………. (i)
and u = x – y ……………(ii)
Adding equations (i) and (ii), we get d + u = 2x
![]() which is the speed of the boat in still water.
which is the speed of the boat in still water.
Subtracting equation (ii) from equation (i), we get d – u = 2y
![]() which is the speed of the steam.
which is the speed of the steam.
The other relations remain the same as in other concepts of time, speed, and distance.
Let us look at some examples.
Example 1: Speed of aman is 10m/s in still water.If the rate of current is 3m/s, find the effective speed of the man upstream.
Solution: Here the speed of the man in still water = x = 10m/s
The speed of the current = y = 3m/s
So, the upstream speed = 10 – 3 = 7m/s
Example 2: Speed of man is 10m/s in still water.If the rate of current is 3m/s, find the effective speed of the man downstream.
Solution:Here the speed of the man in still water = x = 10m/s
The speed of the current = y = 3m/s
So, the downstream speed = 10 + 3 = 13m/s
Example 3: A man row upstream at 10km/hr and downstream at 12 km/hr.Find the man’s rate in still water.
Solution: Here downstream speed = d = 12 km/hr
The upstream speed = u = 10 km/hr
Let the speed of the man in still water = x
So![]()
Example 4: A man row upstream at 10km/hr and downstream at 12 km/hr.Find the rate of water current.
Solution: Here downstream speed = d = 12 km/hr
The upstream speed = u = 10 km/hr
Let the speed of the current = y
So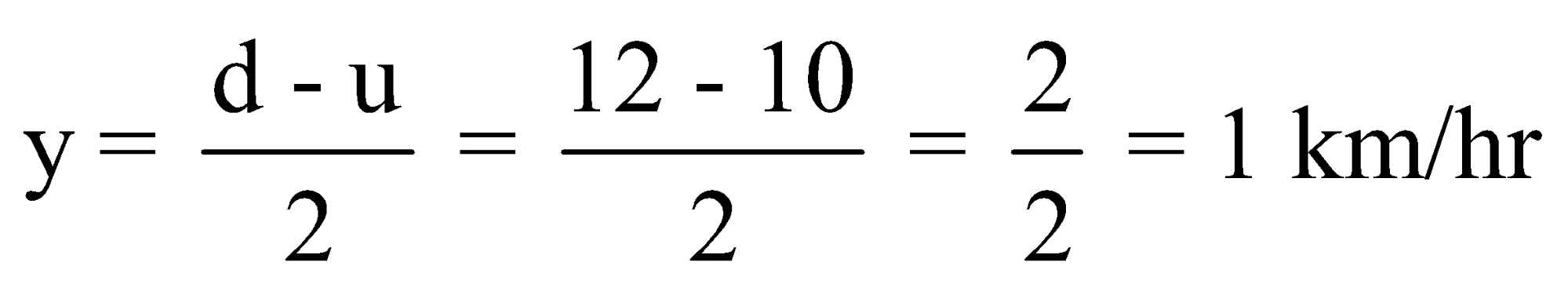
Example 5: A man takes twice as long to row up as to row down the river same distance.If the rate of the river is 6 km/hr,find the rate of the man in still water.
Solution: Let the speed of the man in still water = ‘y’
The upstream speed = y – 6
The downstream speed = y + 6
Let ‘t’ be the time taken to go downstream and 2t be the time taken to go upstream. Since the distance is same, so we have:
2t × (y – 6) = t × (y + 6)
⇒ 2y – 12 = y + 6
⇒ y = 18 km/hr
Solve the exercise given below to get your concept strong.
Exercise:
Question 1: A man rows a boat 18 kilometers in 4 hours downstream and returns upstream in 12 hours. The speed of the stream (in km per hour) is:
(1) 1
(2) 1.5
(3) 2
(4) 1.75
Answer and Explanation
Solution: (2)
Rate downstream ![]() kmph
kmph
Rate upstream =![]() kmph
kmph
Now, speed of the stream![]()
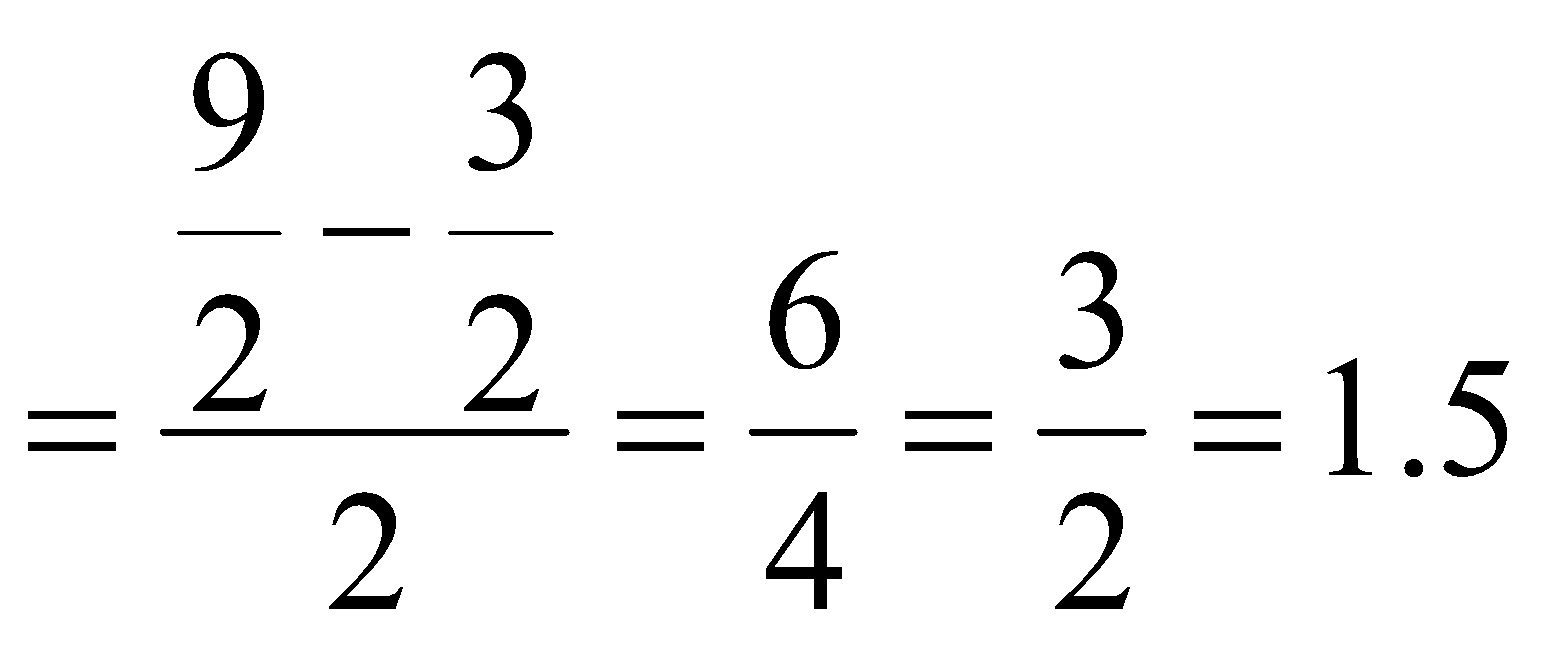 kmph.
kmph.
Question 2: A motorboat in still water travels at a speed of 36 kmph. It goes 56 km upstream in 1 hour 45 minutes. The time taken by it to cover the same distance down the stream will be:
(1) 2 hours 25 minutes
(2) 3 hours
(3) 1 hour 24 minutes
(4) 2 hours 21 minutes
Answer and Explanation
Solution: (3)
Speed of the motorboat upstream
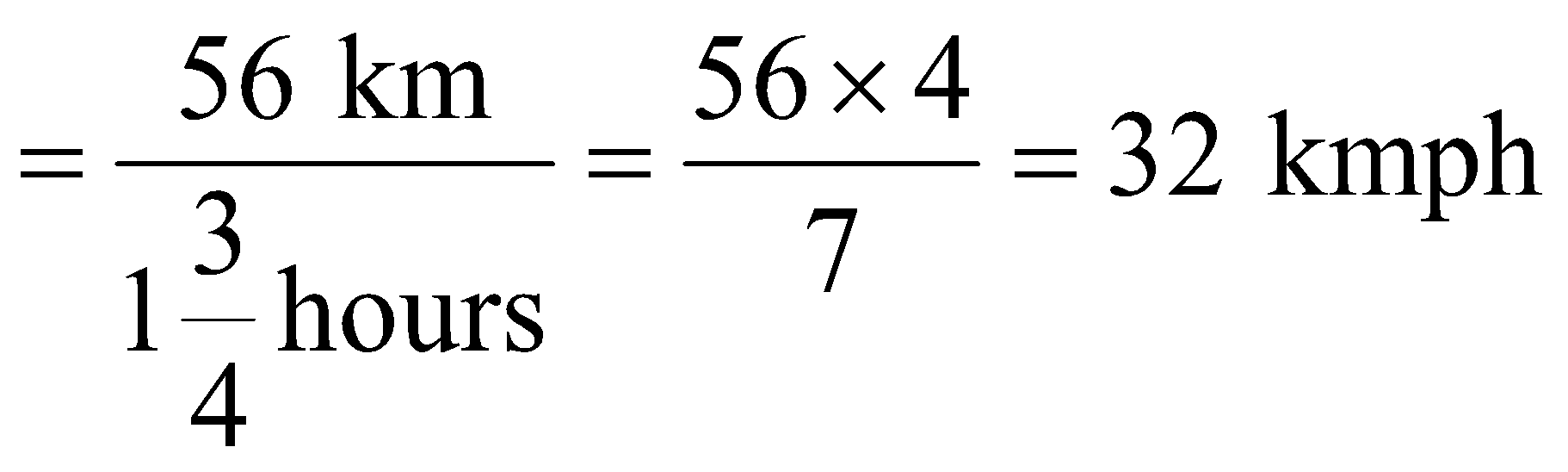
Let the speed of the current = x kmph
Upstream speed of boat BU = BS – WS.
36 – x = 32
Upstream speed= x = 36 – 32 = 4 kmph
Downstream speed of boatBD = BS+ WS.
Speed of motorboat downstream = 36 + 4 = 40 kmph
Time taken to cover 56 km at 40 kmph.
![]() hours
hours
= 1 hours 24 minutes
Question 3: A boat running downstream covers 20 kms in 2 hours while it covers the same distance upstream in 5 hrs. Then speed of the boat in still water is
(1) 7 km/hr
(2) 8 km/hr
(3) 9 km/hr
(4) 10 km/hr
Answer and Explanation
Solution: (1)
Let the speed of boat in still water be x km/hr and that of stream be y km/hr.

Question 4: A boatman rows 1 km in 5 minutes, along the stream and 6 km in 1 hour against the stream. The speed of the stream is?
(1) 3 km/hr
(2) 6 km/hr
(3) 10 km/hr
(4) 12 km/hr
Answer and Explanation
Solution: (1)
Since the boat goes 1 km in 5 minutes, so it will go 12km in one hour.
So, the downstream speed = d= 12 km/hr
Similarly, the upstream speed = u = 6 km/hr
The speed of the stream =![]()
Question 5: A boat covers 24 km upstream and 36 km downstream in 6 hours, while it covers 36 km upstream and 24 km downstream in 6![]() hours. The speed of the current is
hours. The speed of the current is
(1) 1 km/hr
(2) 2 km/hr
(3) 1.5 km/hr
(4) 2.5 km/hr
Answer and Explanation
Solution: (2)
Let the speed of boat in still water = x km/hr
Let the speed of current = y km/hr
Upstream speed of boat = x – y
Downstream speed of boat = x + y
Now we have
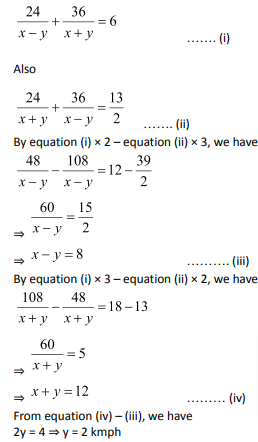
Question 6: The speed of a boat in still water is 10 km/hr. It covers upstream a distance of 45 km in 6 hours. The speed (in km/hr) of the stream is?
(1) 2.5
(2) 3
(3) 3.5
(4) 4
Answer and Explanation
Solution: (1)
Upstream speed of boat ![]() = 7.5 km/hr
= 7.5 km/hr
∴ Speed of current = 10 – 7.5 = 2.5 km/hr
Question 7: A man rows 40 km upstream in 8 hours and 36 km downstream in 6 hours. Then speed of stream is
(1) 0.5 km/hr
(2) 1.5 km/hr
(3) 1 km/hr
(4) 3 km/hr
Answer and Explanation
Solution: (1)
Speed of stream = 0.5 km/hr![]()
Question 8: A boat travels 24 km upstream in 6 hours and 20 km downstream in 4 hours. Then the speed of boat in still water and the speed of water current are respectively
(1) 4 kmph and 3 kmph
(2) 4.5 kmph and 0.5 kmph
(3) 4 kmph and 2 kmph
(4) 5 kmph and 2 kmph
Answer and Explanation
Solution: (2)
Rate upstream = 4 kmph
Rate downstream = 5 kmph
∴ Speed of boat in still water
![]()
= 4.5 kmph
Speed of current = ![]() (5 – 4) = 0.5 kmph
(5 – 4) = 0.5 kmph
Question 9: If a boat goes 100 km downstream in 10 hours and 75 km upstream in 15 hours, then the speed of the stream is
(1) 2 km/hour
(2) 2.5 km/hour
(3) 3 km/hour
(4) 3.5 km/hour
Answer and Explanation
Solution: (2)
Rate downstream = 10 km/hr
Rate upstream = 5 km/hr
∴ Speed of current ![]() (10 – 5) km/hr = 2.5 km/hr
(10 – 5) km/hr = 2.5 km/hr
Speed Time Distance Questions: Problems on Speed Time Distance you should solve for competitive examination preparation
Welcome to this exercise on Speed Time Distance. In this exercise, we build on the basic concepts for Speed Time Distance and focus onboats and streams. As you prepare for your competitive examinations, you will come across questions on Speed Time Distance with focus on boats and streams. Such questions based on boats and streamsneed optimized tackling and can be solved with ease by using simple tricks and understanding the relationships highlighted in this Speed Time DistanceQuestions article. The Speed Time Distance Questions exercise comes into the picture where it gives you a chance to practice the highlighted and important concepts related to this Speed Time Distanceand boats and streamsquestion type.







