Problems based on Viswanathan Anand’s Favourite Game

I do agree that the heading here is a little tongue in cheek and is meant to make you curious about this article. CAT and other MBA entrance exams have featured problems based on grids/chessboards. In these problems, you are suppossed to find the number of sqaures and rectangles for the given grid/chessboard arrangement. At first, you might be baffled by these problems but with diligent practice, you can ace these problems with ease.

With the help of 9 problems, this articles explains the process you need to adopt for solving these CAT chessboard problems.

Question 1:
Find the number of squares which can be formed from 8 cm x 8 cm chessboard?

Solution:
Let us consider a 8cm x 8cm chessboard as shown in the
Figure A in which AB=BC=………=HI=1 cm

Let us calculate those squares which have area 1 cm².
We have 8 such squares in each row and column
Therefore, in totality we have 8×8 = 8² squares

Now we calculate those squares which have area 4 cm²

i.e. we pick those squares having side length 2. Obvious choices are picking squares with sides AC ,BD,CF,DF,EG,FH,GIi.e. 7 possibilities in a row. Similarly 7 choices are(AK,JL,KM,LN,MO,NP,OQ)possible as we move down in a column i.e. sides of length 2cm.So 7 squares in each row and column therefore in totality we have total of 7×7 = 7² squares

Next we calculate those squares which have area 9 cm²

i.e. we pick those squares having side length 3. Obvious choices are picking squares with sides AD ,BE,CF,DG,EH,FI  i.e. 6 possibilities in a row. Similarly 6 choices (AL,JM,KN,LO,MP,NQ) are possible as we move down in a column i.e. sides of length 3cm.So 6 squares in each row and column therefore in totality we have total of 6×6 = 6² squares .
Similarly, number of squares having side length 4 will be 5² squares

Similarly, number of squares having side length 5 will be 4² squares

Similarly, number of squares having side length 6 will be 3² squares

Similarly, number of squares having side length 7 will be 2² squares

Similarly, number of squares having side length 8 will be 1² squares

Thus total number of squares =8²+7²+6²+5²+4²+3²+2²+1² = (8 x 9 x 17)/6 = 204

GENERALISATION:

 Number of squares which can be formed from N x N chessboard

Question 2:
Find the number of rectangles which can be formed from 8 cm x 8 cm chessboard?

Solution:
METHOD 1
We first calculate rectangles of size 8×8 clearly it will be only
1 such rectangle i.e. the whole of chess board.
Now we calculate rectangles of size 1×2
Let us understand this in detail:
If we fix one side as AJ (1 cm), then possibilities of other side of rectangles are AC ,BD,CF,DF,EG,FH,GI  i.e. 7 possibilities .
Similarly for JK,KL,…………..,PQ we have 7 possibilities each. Therefore, in totality 8 x7 rectangles of size1x2 are possible.
Analogous to this we can directly say rectangles of size 2×1 will be 7×8
Now we calculate rectangles of size 1×3
Let us understand this in detail ,if we fix one side as AJ (1 cm) .Then possibilities of other side of rectangles are AD ,BE,CF,DG,EH,FI  i.e. 6 possibilities .
Similarly for JK,KL,…………..,PQ we have 6 possibilities each. Therefore in totality 8 x6 rectangles of size
1×3 are possible
Analogous to this we can directly say rectangles of size 3×1 will be 6×8

Similarly rectangles of size 1×4 will be 8×5 and rectangles of size 4×1 will be 5×8 and so on.
Hence total number of rectangles will be
8(1+2+3+….+8)+7 (1+2+3+….+8)+………………..+1(1+2+3+….+8)
=(1+2+3+….+8)(1+2+3+….+8)

GENERALISATION:

 Number of rectangles which can be formed from N x N chessboard

= (1+2+3+….+N)(1+2+3+….+N)

Question 3:
Find the number of pure rectangles which can be formed from 8 cm x 8 cm chessboard?

Solution:
We calculated earlier, Number of rectangles formed in 8 cm x 8 cm chessboard=1296
Number of squares in 8 cm x 8 cm chessboard=204
Thus number of pure rectangles = No. of rectangles – No. of Squares=1296 – 204=1092.
The next obvious generalization which can be done on the basis of what we learnt above is

GENERALISATION:
Number of Pure Rectangles which can be formed from N x N chessboard
=(1+2+3+….+N)(1+2+3+….+N)   –   (1²+2²+3²+4²+…………………..+N²)

Question 4:
Find the number of parallelograms which can be formed from 8 cm x 8 cm chessboard?

Solution:
We know parallelogram is such a figure in which opposite sides are parallel
Out of the given 9 parallel HORIZONTAL lines we can choose any two lines which can be done in ⁹C₂ ways. Similarly,

Out of the given 9 VERTICAL set of parallel lines we can choose any two lines which can be done in ⁹C₂ways.

Thus total number of parallelograms which can be formed using these lines =

NOTE: The answer is same as it was in Question 2 .Thus we conclude that number of rectangles and number of parallelograms formed in case of chess board is same.

GENERALISATION: 

There are two sets of parallel lines containing m and n lines respectively. Number of parallelograms that can be formed using these lines is

Question 5:
Given is a road map of a city in form of chess board (as shown in figure A). Find the number of different paths that a person can take to reach from one corner to diagonally opposite corner of the city  (From corner Q to I)?

Solution:
Let us take simplest path in going from to Q to I by taking straight road from Q to A then straight road from A to I i.e. he goes from
QP -> PO ->ON->NM->ML->LK->KJ->JA->AB -> BC ->CD->DE->EF->FG->GH->HI
Notice that he took 8 vertical steps (VVVVVVVV where V denotes vertical step) and 8 horizontal steps(HHHHHHHH where H denotes horizontal steps)i.e. he moved in following manner
VVVVVVVVHHHHHHHH
Or even if person chooses some other path as well then also it will involve 8 vertical steps or 8 horizontal steps arranged in some other pattern
We know the no. of ways of arranging the word with 8 V and 8 H are 16!/8!8!

So the required number of paths = 16!/8!8!

Question 6:
Given is a road map of a city in form of chess board (as shown in figure B where a portion in between is darkened to depict that in between roads are under construction). Find the number of different paths that a person can take to reach from A to X first then from Y to B under the condition that a person cannot take in between roads which are under construction?

Solution:

Let us calculate the number of ways a which a person can go from A to X
In going from A to X a person will take 3 horizontal steps (HHH where H denotes horizontal steps)and 3 vertical
VVV where V denotes vertical step) i.e. he moved in following manner
VVVHHH

We know that the no. of ways of arranging the word with 3 V and 3 H are 6!/(3! x 3!) = 20 ways
Now as per the given question, in between roads are under construction so he cannot take in between roads which are under construction. So, there  are only 2 ways to go from X to Y i.e. from X ->P->Y or X ->Q->Y
In going from Y to B a person will take 2 horizontal

steps (HH where H denotes horizontal steps)and 2 vertical(VV where V denotes vertical step) i.e. he moved in following manner VVHH.

We know the number of ways of arranging the word with 2 V and 2 H are 4!/(2!x2!) = 6 ways

Thus, the total number of ways in going from A to B = 20 × 2 × 6 = 240.

Question 7:
Two squares are chosen at random from small squares drawn on a chess board. Find the number of ways in which 2 squares can be chosen such that they have exactly one corner in common?

Solution:
Two squares selected can have a corner common if they are selected from two consecutive rows or columns. The number of ways to select two consecutive rows(or columns) are 7.
For each pair of two consecutive rows(or columns),the number of pairs of squares having exactly one common corner =2× 7=14 ways
Total number of selections = 14× 7 =98

Question 8:
Find the number of ways in which a white and a black square on a chess board be chosen so that two squares do not belong to same row or column?

Solution:
In a standard chess board we have 32 white squares and 32 black squares.Thus, any white square can be chosen in 32 ways and once a particular white square is chosen we cannot pickany other square from that particular row or column(i.e. in that row or column we will have 4 black and 4 white squares)Hence, we are left with 32 – 8 = 24 squares. Therefore , the number of ways in which a white and a black square on a chess board be chosen so that two squares do not belong to same row or column are 32 ×24 =768.

Question 9:
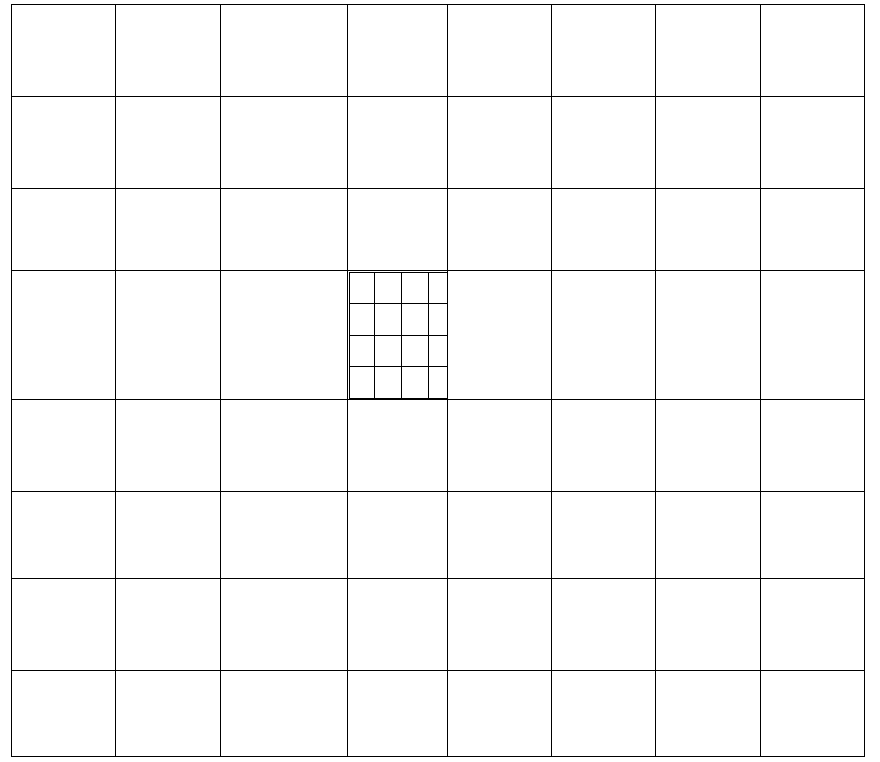
In the given Grid(A Chessboard designed in such a way that middle square of outer chess board of 8×8 contains 1 more smaller grid of dimension 4×4 ), Find the number of squares of all possible dimensions?

Solution: 

Clearly the number of squares in the outer 8×8 chess board = 8²+7²+6²+5²+4²+3²+2²+1² =204

Clearly the number of squares in the inner 4 x 4 grid = 4²+3²+2²+1²=30

But one square is common. Thus, required number of squares =204+30 -1 =233.

Please Note: This article is written by a 100-percentiler in CAT 2016. He is a director of a leading test-prep institute and is the best person to learn Mathematics from. In fact, he was the trainer for Wordpandit himself and Wordpandit credits a lot of his learning to this Master Trainer. Dig into this amazing article by this Mathematics Wizard. We will reveal his identity in the coming posts..:)