What is Compound Interest? Let’s explore the basic concepts for Compound Interest
Compound Interest is part of the wider topic of Interest. In the first part of this topic, we learned about Simple Interest. Well, simple interest is not the only interest mechanism used by lenders and borrowers. There is another method, one which actually runs majority of business operations and goes by the name of Compound Interest.
The basic concept operating behind compound interest is very simple. Let us take a small example to understand its rudiments:
Sham borrows a sum of Rs. 100 from Ghansham for a period of two years. The rate of interest for this loan is 10%. At the end of year one, the amount due is the principal and 10% interest on it, that is a total of Rs. 110. Now, effectively the principal value of the loan for the second year is no longer Rs. 100, it is in fact Rs. 110. That is what Ghansham would say and believe. According to him, for the 2nd year, he has lent Rs. 110 as that was the amount he would have had if he taken back the money at the end of year 1. Now for the 2nd year, the interest becomes Rs 11 (10% of Rs. 110) and the total amount Ghansham would get at the end of the second year will be Rs. 121.
If the same calculation was done using the logic of simple interest, you would see that the interest due for two years would be Rs. 20 (10% of Rs 100 for two years). Thus, replace a S with a C and there is such a big difference in the calculations carried out.
This covers the basic introduction for Compound Interest. Now let’s go through some basic concepts and acquaint ourselves with the mechanics of this topic.
Compound Interest Definitions
Four basic definitions that you need to know in order to figure out
Principal (P): The original sum of money loaned/deposited. Also known as capital.
Interest (I): The amount of money that you pay to borrow money or the amount of money that you earn on a deposit.
Time (T): The duration for which the money is borrowed/deposited. The duration does not necessarily have to be years. The duration can be semi-annual, quarterly or any which may be deemed fit.
Rate of Interest (R): The percent of interest that you pay for money borrowed, or earn for money deposited.
Compound Interest Formula:
Time for the actual learning to begin and you should learn the formula for Compound Interest.
Amount Due at the end of the time period is given by
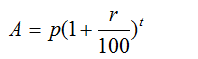
Where:
P: Principal (original amount)
R: Rate of Interest (in %)
T: Time period (yearly, half-yearly etc.)
The Compound Interest over the time period T is given by by the formula:
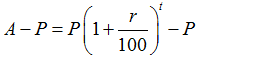
This can be written as:
Compound Interest= P {(1+r/100)t -1}
Useful Tip: In case of simple interest, principal and interest remain same for every year while in case of compound interest, the amount at the end of each year will be the principal for next year and interest for different years is not the same.
Example 1: Maninder took a loan of Rs. 10000 from Prashant. If the rate of interest is 5% per annum compounded annually, find the amount received by Prashant by the end of three years
Solution: The following is the data given:
Principal, P= 10000
Rate = 5%
Time =3 years
Using the formula for Compound Interest:
A = P(1+R/100)t
So A= 10000(1+5/100)3
A = 10000(1+1/20)3
A = 10000 x 21/20 x 21/20 x21/20 =11576.25
So, the total amount paid by Maninder at the end of third year is Rs.11576.25
Example 2: Richa gave Rs. 8100 to Bharat at a rate of 9% for 2 years compounded annually. Find the amount of money which she gained as a compound interest from Bharat at the end of second year.
Solution:
Principal value = 8100
Rate = 9%
Time = 2 years
So the total amount paid by Bharat
= 8100(1+9/100)2
=Rs. 9623.61
The question does not probe the amount, rather, it wants to know the CI paid, that the difference between the total amount and original principal.
The Compound Interest = 9623.61 – 8100 = 1523.61
Simple Interest vs Compound Interest: Difference between simple interest and compound interest
Simple Interest and Compound Interest are both related to the wider topic of interest. Even though these two are two types of interests on a certain sum or quantity, there is a marked difference between the two. When compounding is done on a sum of money, then the interest for the first year also gets added to the principal while calculating the interest payout for the second year. This happens for all subsequent years or the time duration when the interest is being levied (effectively, interest is being charged on interest itself).
In case the same principal P is invested in two schemes, at the same rate of interest r and for the same time period t, then in that case:
Simple Interest = (P x R x T)/100
Compound Interest = P [(1+R/100)T – 1]
So, the difference between them is
= P[(1+R/100)T -1] – PRT/100
= P [(1+R/100)T -1-RT/100]
Two Useful Shortcuts based on the above concept:
Difference between CI and SI when time given is 2 years = P(R/100)2
Difference between CI and SI when time given is 3 years = P[(R/100)3 + 3(R/100)2

If difference and principal is given, you can easily calculate rate % from this formula.
Example 3: The difference between compound interest and simple interest is 2500 for two years at 2% rate, then find the original sum.
Solution:
Given difference is = 2500
So, Simple Interest = (P X R X T)/100
Compound Interest = P [(1+R/100)t – 1]
So the difference between both of them is
= P[(1+R/100)T -1] – PRT/100
= P [(1+R/100)T -1-RT/100]
2500 = P [{(1+2/100)2-1}-4/100]
On simplification this equation, the sum will be = Rs. 6250000
Let’s use the shortcut method:
When time given is 2 years, Difference = P(R/100)2
Since the difference given is Rs 2500, we have
2500 = P (2/100)2
=> 2500 = P (1/50)2
=> 2500= P (1/2500)
=> 6250000=P
So, the sum is Rs.6250000.
Compound Interest Exercises: Questions and Answers featuring Basic Compound Interest problems
In the following section, we solve 5 questions that are based on the basics of Compound Interest. You will solve some compound interest questions in this section and with the help of these questions, you will be able to learn the basic concepts for this topic. Remember, learning a topic such through solved problems and questions is the best approach possible.
Question 1: An amount of Rs 1000 is borrowed at CI at the rate of 2% per annum. What will be the amount to be paid after 3 years if the interest is compounded annually?
A. 926.24
B. 1248.34
C. 1061.28
D. 1678.34
Answer and Explanation
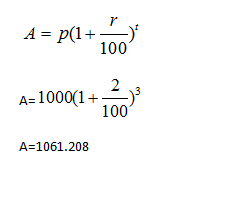
Question 2: An amount of Rs 1000 amount equates to Rs 1728 in 3 years when interest is compounded annually. What will be the rate per annum?
A. 24%
B. 20%
C. 18%
D. 16%
Answers and Explanation
Using Formula
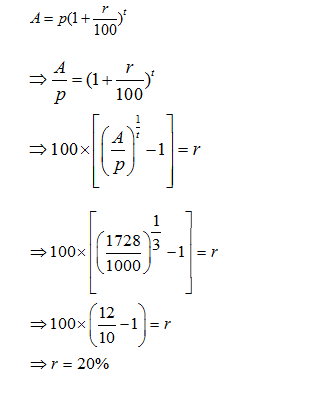
Question 3: The difference between the compound interest and the simple interest on a certain sum at 4% rate for 2 years is Rs 100. What will be the amount invested?
A. 45500
B. 52500
C. 62000
D. 62500
Answer and Explanation
The difference between compound interest and simple interest for two years is given by
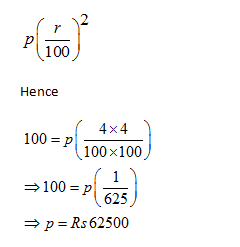
Question 4: The difference between the compound interest and the simple interest on a certain sum at 4% rate for 3 years is Rs 100. What will be the amount invested?
A. 20559
B. 25559
C. 16559
D. 28559
Answer and Explanation
The difference between CI and SI for three years is given by
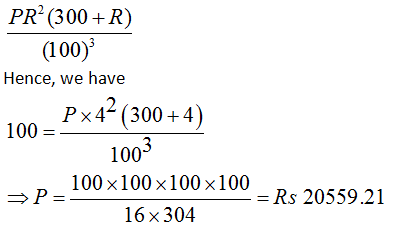
Question 5: A sum of money invested at compound interest amounts to Rs. 650 at the end of first year and Rs. 676 at the end of second year. The sum of money is:
A. Rs. 600
B. Rs. 540
C. Rs. 625
D. Rs. 560
Answer and Explanation
Simple Interest for one year = Compound Interest for one year
Interest on Rs. 650 for 1 year = 676 –650 = Rs. 26
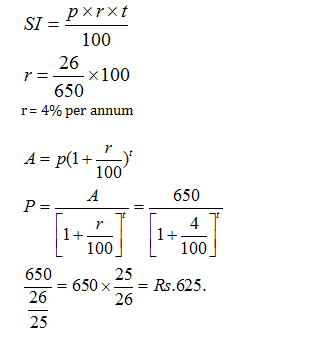










Complete an amortization schedule for a €20,500 loan to be repaid in equal installments at the end of each of the next 3 years. The interest rate is 4%, compounded annually.
Thanks a lot wordpandit. I really liked this site and I have recommended it to my friends too. Keep up the good work.
Thank you so much for sharing this concept I am feeling helpful because of this page thank you so much again.
Question 2 have problem in place of 2 year there should be three.
Thanks Manish
We made the change
Regards
Wordpandit