Learn the applications of for the topic through Compound Interest Examples
The first article for compound interest was all about the basics and essentially explained the compount interest formula. In this article, we use compound interest examples in order to understand important concepts and applications related to Compound Interest.
What all do we cover in this compound interest examples article?
We cover:
- The concept of equal installments
- Application of Compound Interest to population growth problem
- Negative compound interest
Compound Interest Installments: Concept of Equal Installments
How does the concept of equal installments work for Compound interests? Well, in this case, the problem basically tells us that a certain sum of money is borrowed on compound interest for a certain period and it is returned with the help of equal installments.
Let us derive a formula where the amount is returned in two equal installments for a time period of two years.
Assume P to be the principal and r the rate of interest.
Step 1: P[{1+r/100}]= PI (amount of one year)
Step 2: New Principal
Now let X be the first installment. After giving the first installment, the principal value will change and the new principal will be = P1 – X
Step 3: Amount and Interest for the second year
Now the interest charged will be charged on this amount.
Amount at the end of second year is P2 = (P1 –X ){1+r/100}
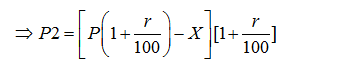
Step 4: Since the installments are equal, this new amount has to be equal to X.
Hence,
[P(1+r/100)-X][1+r/100]=X
On solving, we have
P (1+R/100)2-X (1+R/100)]= X
P (1+R/100)2]= X+X (1+R/100)
Divide both sides by (1+r/100)2
So we are left with:
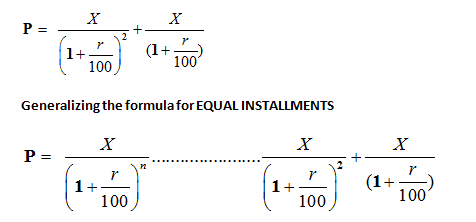
where X is the installment and n refers to the number of installments.
Compound Interest Examples: Let’s solve an example question to understand the compound interest questions.
Question-1: Richa borrowed a sum of Rs. 4800 from Ankita as a loan. She promised Ankita that she will pay it back in two equal installments.If the rate of Interest be 5% per annum compounded annually, find the amount of each installment.
Solution:
Given that principal value = 4800
Rate =5%
Two equal installments annually = 2 years
Appling the formula, P = X/(1+r/100)n…………………….X/(1+r/100)
So, we have here two equal installments.
P= X/(1+r/100)2 + X/(1+r/100)
4800=X/(1+5/100)2 + X/(1+5/100)
On simplifying
We have x= Rs. 2581.46
So, the amount of each installment is Rs 2581.46
Compound Interest Examples: Use of Compound Interest for concepts of population growth.
We study two compound interest examples in this section where we study the concept of population growth. These are particular types of compound interest problems and we are going to explain how you approach these questions. Let’s take up one case at a time and then take up some compound interest examples questions to understand these concepts.
Case 1: When population growing in a constant rate
If the population increases with a constant rate say by r% then the population after T years will be
= P (1+R/100)t
In fact, this is nothing else but an application of the fundamentals of compound interest.
It is actually similar to finding the compound amount after time T years
Net population after T years = = P (1+R/100)t
Net population increase = P [(1+R/100)t– 1]
Example 2:The population of Chandigarh is increasing at a rate of 4% per annum. The population of Chandigarh is 450000, find the population in 3 years hence.
Solution:
P = 450000
Rate of increasing = 4%
Time =3 years
Therefore, the total population after 3 years will be
T = P (1+R/100)3
=> T = 450000(1+4/100)3
=> T = 506188
Case 2: When the population growing with different rates and for different intervals of time
If the rate growth of population increased with different rate and for different intervals of time then the population after T years will be =
P (1+R1/100)t1x (1+R2/100)t2…………………………….. (1+RN/100)tn
Let us take an example for this concept.
Example 3:The population of Chandigarh increased at a rate of 1% for first year, the rate for second year is 2%, and for third year, it is 3%. Then what will be the population after 3 years if present population of Chandigarh is 45000?
Solution:
Since the rate growth of population increased with different rates for the three difference years, the population after T years will be =
P (1+R1/100)t1 x (1+R2/100)t2x (1+R3/100)t3
45000(1+1/100)1 x (1+2/100)1 x (1+3/100)1=47749.77» 47750
Case 3: When the population is decreasing with rate R
Population after a time period of T years=P (1-R/100)t
Where P is the initial population
R is rate at which the population is decreasing
Example 4:The population of Chandigarh is increases at a rate of 1% for first year, it decreases at the rate of 2% for the second year and for third year it again increases at the rate of 3%. Then what will be the population after 3 years if present population of Chandigarh is 45000?
Solution:
The rate growth of population increases, then decreases for the second year and again it increases for third year.
The population after T years will be
=P (1+1/100)x (1-2/100)x (1+3/100)
=45000(1+1/100)1 x (1-2/100)1 x (1+3/100)1=45877.23» 45877
This completest the section on population growth problems. Hope with the help of above compound interest examples, you have been able to understand how these problems need to be approached.
Tooltip 3: Negative Compound Interest
As we can see from the last case above, it is not necessary that there is always an increase in any quantity or amount. There can also be a reduction in the amount of something. This reduction is called the rate of depreciation, especially in the financial world. In this case, we do nothing else but take the interest rate to be negative. The formula for this is as follows:
Let P be the original amount.
Let P1 be the new amount at the end of t years.
P1 = P (1-R/100)t
Here R is the rate of interest (negative rate).
Always remember, the rate of depreciation is nothing else but negative rate of interest.
Example 5: Manpreet bought a new car. The value of the car is Rs. 45000. If rate of depreciation is 10% per annum then what will be the value of the car after 2 years
Solution:
Here P = 45000
Rate of depreciation = 10%
T = 2 years
Therefore, the value will be after 2 years = P (1 – R/100)t
= 45000(1-10/100)2
=Rs 36450
Questions on Compound Interest: Practice Questions
In order to understand the concepts mentioned above, it is best to practice some questions on compound interest and understand the applications for this topic. Solve five compound interest examples and perfect your learning.
Question 1: A builder borrows Rs. 2550 to be paid back with compound interest at the rate of 4% per annum by the end of 2 years in two equal yearly installments. How much will each installment be?
A. Rs. 1352
B. Rs. 1377
C. Rs. 1275
D. Rs. 1283
Answer and Explanation
Amount = Rs 2550
Rate = 4% per annum
Time = 2 years
Applying the formula
P= X/(1+r/100)n+ …………………….X/(1+r/100)
Here we have two equal installments, so
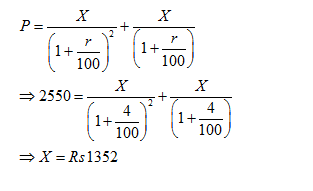
Question 2: A man buys a scooter on making a cash down payment of Rs. 16224 and promises to pay two more yearly installments of equivalent amount in next two years. If the rate of interest is 4% per annum, compounded yearly, the cash value of the scooter, is
A. Rs. 40000
B. Rs. 46824
C. Rs. 46000
D. Rs. 50000
Answer and Explanation
Concept used in this question is: you need to calculate principal for every year unlike simple interest where principal used to be same for every year.
Let principal (present worth) for first year be P1 and that for two years be P2.
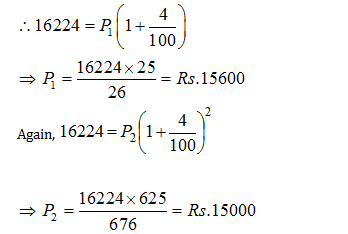
The total payment will be ( cash down payment + installments paid )
Cash value of the scooter
= Rs. (16224 + 15600 + 15000) = Rs. 46824.
Question 3: Kamal took Rs. 6800 as a loan which along with interest is to be repaid in two equal annual installments. If the rate of interest is 25/2 %, compounded annually, then the value of each installment is
A. Rs. 4200
B. Rs. 4150
C. Rs. 4050
D. Rs. 4000
Answers and Explanations
Let the annual installment be Rs. z.
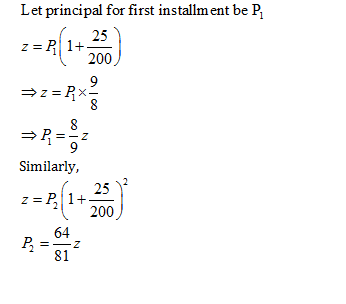
Now
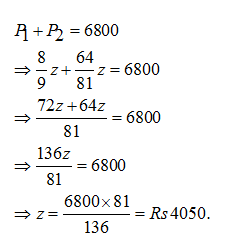
Question 4: The population of Chandigarh is increases at a rate of 1% for first year, it decreases at the rate of 4% for the second year and for third year it again increases at the rate of 5%. Then what will be the population after 3 years if present population of Chandigarh is 50000.
A. Rs. 51006
B. Rs. 50904
C. Rs. 50836
D. Rs. 51125
Answers and Explanations
Since the rate growth of population is increasing first and then decreasing for the second year and again it increases for third year, then the population after T years will be
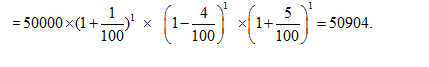
Question 5: A person bought a new machine. The value of the machine is Rs. 10000. If rate of depreciation is 5 % per annum, then what will be the value of the machine after 2 years?
A. Rs. 9025
B. Rs. 9044
C. Rs. 9110
D. Rs. 9080
Answer and Explanation
Here P = Rs 10000
Rate of depreciation = 5%
T = 2 years
Therefore, the value after 2 years will be= P (1 – R/100)t
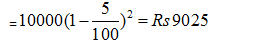








Merci!
Compound Interest Installments: Concept of Equal Installments
Step 4:Since the installments are equal, this new amount has to be equal to X.
Hence,
[P(1+r/100)-X][1+r/100]=X
On solving, we have
P [(1+R/100)2-X (1+R/100)] = X–> why does this equation has a square as compared to previous equation? (I.e there is a square in (1+R/100)^2 while in previous equation it is simply (1+r/100))
Here not that the term in the second bracket i.e. 1+r/100 is multiplied with P(1+r/100) term of the 1 bracket resulting in P (1+r/100)^ while there should not be square bracket after P in step 4 after while solving, though its a small punctuation error and the correct form can be easily picked by further steps!