Compound Interest Shortcuts, Tricks, Tips & Results-2
In this article, we pick up from where we left in the previous article and cover Compound Interest Shortcuts that you can employ in exams. We cover an extremely useful set of compound interest shortcuts, tips, tricks, and results. You can use these Compound Interest tips and Compound Interest shortcuts in competitive exams and make sure save some vital time in the examination by employing these techniques.
Kindly keep in mind that the purpose of this article is to provide you with useful compound interest shortcuts and tips. This article does not cover any core concepts for this topic. For compound interest concepts, you should refer to the first two articles for this topic. Also, some of these compound interest shortcuts might appear obscure or too formula-based to you. Remember, you need to learn these compound interest shortcuts with a pinch of salt. All of these might not be applicable and in fact, you might not be able to learn and remember all of them. It is best to be selective with these compound interest shortcuts and use them to the best of your ability.
In each of the following results, we use the following denotations:
A = future value
P = principal amount (initial investment)
r = annual nominal interest rate
n = number of times the interest is compounded per year
t = number of years for which the money is borrowed
Let’s get started and cover some of these shortcuts.
Compound Interest Shortcuts: Tooltip-1
A sum of money placed at compound interest becomes x time in ‘a’ years and y times in ‘b’ years. These two sums can be related by the following formula:
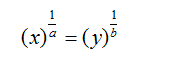
Derivation for this result:
We use the basic formula for calculating Compound Interest:
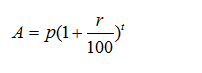
For condition 1, a sum of money becomes x times in “a” years.
Therefore, using the formula for calculating Compound Interest:
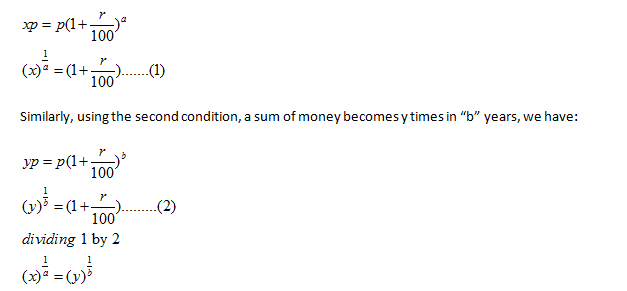
Example-1: A sum of money placed at compound interest doubles itself in 4 years.In how many years will it amount to 16 times itself?
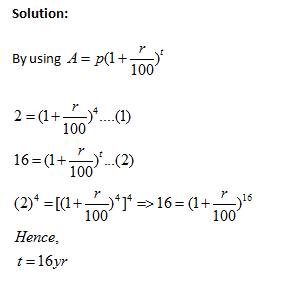
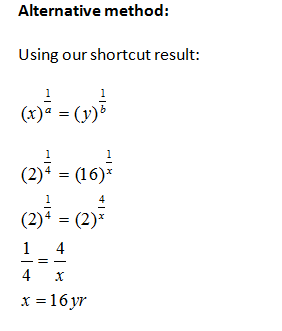
Compound Interest Shortcuts: Tooltip 2
If an amount of money grows up to Rs x in t years and up to Rs y in (t+1) years on compound interest, then
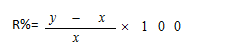
Derivation for this result:
Principal + CI for t years = x …… (1)
Principal + CI for (t+1) years= y ……. (2)
(2) – (1) =>CI for last year = y-x
Which is basically the simple interest upon x
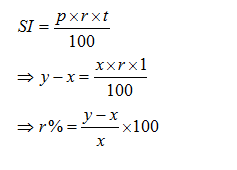
Example-2: An amount of money grows upto Rs 3000 in 3 years and upto Rs 4000 in 4 years on compound interest. What will be the rate percent?
Solution:
Principal + CI for 3 years = 3000 …… (1)
Principal + CI for 4 years= 4000 ……. (2)
Hence (2) – (1) =>CI for 4th year = 4000-3000= Rs 1000
Which is basically the simple interest upon 3000
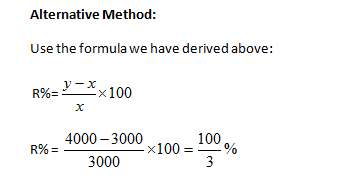
Compound Interest Shortcuts: Tooltip 3
A sum at a rate of interest compounded yearly becomes Rs. A1 in n years and Rs. A2 in (n + 1) years, then
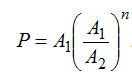
Example-3: A sum of money invested at compound interest amounts to Rs. 100 at the end of first year and Rs. 120 at the end of second year. The sum of money is :
Solution:
Simple Interest for one year = compound interest for one year
Interest on Rs. 100 for 1 year = 120-100= Rs. 20
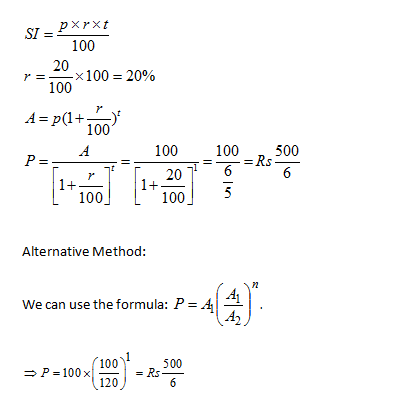
Compound Interest Shortcut: Tooltip 4
If a certain sum becomes x times of itself in t years, the rate of compound interest will be equal to
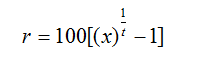
Derivation for this result:
Use the formula for Compound Interest Calculation:
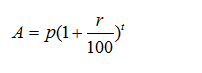
Sum becomes x times of itself in t years so
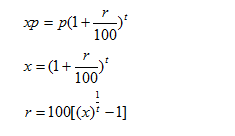
Example 4: If a certain sum becomes 16 times in 2 years ,what will be the rate of compound interest?
Solution:
Using the formula derived above:
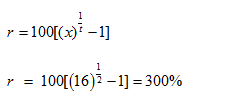
Compound Interest Shortcut: Tooltip 5If the compound interest on a certain sum for 2 years is CI and simple interest for two years is SI ,then rate of interest per annum is
If the compound interest on a certain sum for 2 years is CI and simple interest for two years is SI ,then rate of interest per annum is
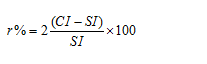
Derivation for this result:
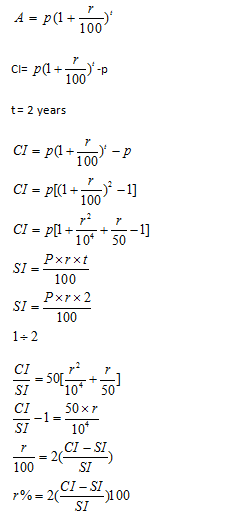
Example 5: If the compound interest on a certain sum for 2 years is 20rs and simple interest for two years is 10rs ,then what wil be the rate of interest per annum ?
Solution:
Using the formula derived above:
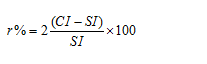
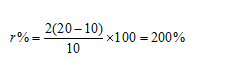
Compound Interest Solved Problems using Compound Interest Shortcuts:
Let’s go through some compound interest solved problems and learn how to use and implement compound interest shortcuts in actual problem solving. Remember, till the time you actually solve questions using these tricks, you won’t be able to memorize and understand them. Go through compound interest solved problems and hone your skills for the topic.
Question 1: What sum of money at compound interest will amount to Rs. 650 at the end of the first year and Rs. 676 at the end of the second year?
A. Rs. 600
B. Rs. 600.25
C. Rs. 625
D. Rs. 625.25
Answers and Explanations
Using the formula we have derived in the article for this exercise:
If an amount of money grows up to Rs x in t years and up to Rs y in (t+1) years on compound interest, then
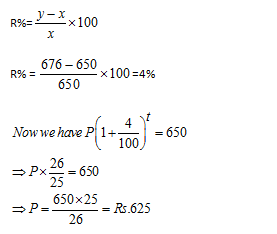
Question 2: If the amount is 2.25 times of the sum after 2 years at compound interest (compound annually) , the rate of interest per annum is :
A. 25%
B. 30%
C. 45%
D. 50%
Answers and Explanations
Using the formula we have derived in the article for this exercise:
If a certain sum becomes x times of itself in t years, the rate of compound interest will be equal to
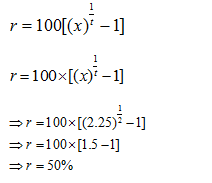
Question 3: A sum of money doubles itself in 4 years at compound interest. It will amount to 8 times itself at the same rate of interest in:
A. 18 years
B. 12 years
C. 16 years
D. 24 years
Using the formula we have derived in the article for this exercise: A sum of money placed at compound interest becomes x time in ‘a’ years and y times in ‘b’ years. These two sums can be related by the following formula:Answes and Explanations
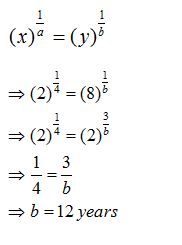
Question 4: A sum borrowed under compound interest doubles itself in 10 years. When will it become fourfold of itself at the same rate of interest?
A. 15 years
B. 20 years
C. 24 years
D. 40 years
Answers and Explanations
Using the formula we have derived in the article for this exercise:
A sum of money placed at compound interest becomes x time in ‘a’ years and y times in ‘b’ years. These two sums can be related by the following formula:
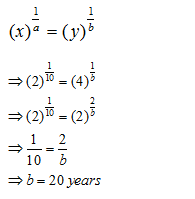
Question 5: A sum of money becomes eight times of itself in 3 years at compound interest. The rate of interest per annum is
A. 100%
B. 80%
C. 20%
D. 10%
Answers and Explanations
Let the principal be Rs. x and the rate of compound interest be r% per annum.
Then,
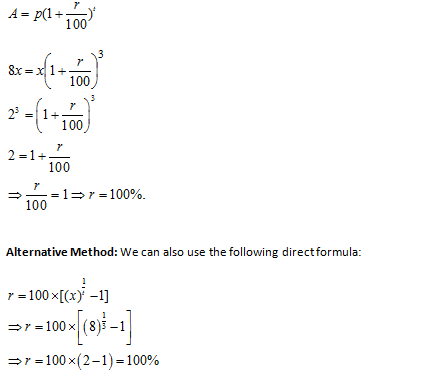








Simply nice tricks .👍👌👌
Upload some more…
I face problem in cset math
It is very useful and easy to understand. Thanks
Thank-you.very helpful.
In Q1 Alternate method is wrong and an answer for entirely different question, please change it.
Hey Arun
Thanks for the input. The image from the previous article was carried forward here by mistake. We have made the update.
Regards
Wordpandit