Divisibility rules for composite numbers

How do we proceed when we are asked to check whether a composite number is divisible by a given number or not? It can be done using a simple method.

Method:

Step 1: factorize the number.

Step 2: The number will be divisible by the composite divisor when the number is divided by all the factors at once.

Divisibility check for number 6:

Step 1: factorize 6; 6=2*3

Step 2: Now the number we want to check divisibility for should be divided by 2 and 3 both

Example: Check whether 84846 is divisible by 6.

Solution:  Factors of 6 = 2*3

According to above rule if 84846 will be divided by both 2 and 3, only then it will be divisible by 6 .

Divisibility check for 2:  check the last digit of the given number. If it is even then the number will be divisible by 2.

84846 has even unit digit. So it will be divisible by 2.

Divisibility check for 3: Number is divisible by 3 if the sum of all the digits of number is divisible by 3.

Sum of digits of 84846 => 8+4+8+4+6=30 => 3+0=3

3 will be divisible by 3.

So 84846 will be divisible by 3.

Because 84846 is divisible by 2 and 3 both so it will be divisible by 6.

Divisibility test for 12:

Step 1:  Factorize 12 =>    12=2*2*3  ;   12=

Step 2: To check divisibility the number should be divisible by 2² /4   and 3

 Example: Check whether 158496 is divisible by 12.

Solution: The number should be divisible by 4 and 3 if it has to be divisible by 12.

Divisibility check for 3- Number is divisible by 3 if the sum of all the digits of number is divisible by 3.

Sum of digits of 158496 =>  1+5+8+4+9+6 =33

Which is divisible by 3

Divisibility check for 4- Check for last 2 digits of number, if 2 digits can be divided by 4 then the number will be divided by 4.

Last two digits are 96 that are divisible by 4.

Because the number is divisible by both 4 and 3 so the number will be divisible by 12.

Divisibility test for 26 :-

Step 1- factorize 26; 26 = 13*2

Step 2- the number should be divisible by both 13 and 2

Example: check whether 10452 is divisible by 26 .

Solution: Factors of 26 = 13*2

Divisibility check for 2– Check the last digit of the given number. If it is even then the number will be divisible by 2.

10452 has even unit digit .so it will be divisible by 2 .

Divisibility check for 13- seed no. for 13 is -9 or 4

Now follow the process explained under “ divisibility check for prime numbers”

Unit digit of 10452 is 2;  2*-9 =-18

1045+(-18) =1027

Unit digit of 1027; 7*-9 =-63

102+(-63) =39

39 is divisible by 13, so the number will be divisible by 13.

Now the number is divisible by 13 and 2, it will be divisible by 26 too.

Let us practice some questions.

 

EXERCISE:

Question 1: The total number of integers between 100 and 200, which are divisible by both 9 and 6, is:

(1) 5                      (2) 6                      (3) 7                      (4) 8

 

Question 2: The total number of 3-digit numbers that are exactly divisible by 6 is:

(1) 149                                (2) 150                                (3) 151                                (4) 166.

 

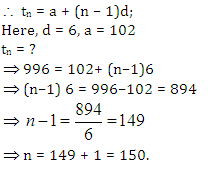
Question 3: If a number is divisible by both 11 and 13, then it must be necessarily:

(1) Divisible by (11+13)             (2) Divisible by (13 –11)

(3) Divisible by (11 × 13)           (4) 429

 

Question 4:  * is a digit such that 5824* is divisible by 11, then * equals:

(1) 2                      (2) 3                      (3) 5                      (4) 6