In this article, we will see what exponents really are and go through some tips to solve the exponential expressions. Exponents also go by the name of powers and indices. So in case you find any of these words used interchangeably in various texts, be rest assured they refer to the same.
Basic Definition of Exponents
Exponents are a method that is used to express products of the same number.
How would you write: 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2?
Hard to repeat the above number in calculations, isn’t it?
Well, exponents provide us the solution to the above problem. The above number simply becomes: 29
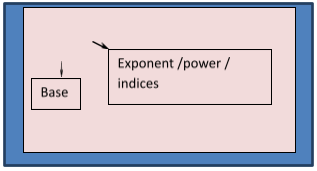
For the expression AN:
- A is called the base
- N is called the exponent
It is generally read as A to the power N.
Essentially, we can say![]()
The reverse of the exponent form is the product form.
Example: How would you write ![]() in product form?
in product form?
Solution: We know ![]() =5x5x5
=5x5x5
Negative exponent: As we have seen above, exponent refers to essentially multiplication of a number with itself. In the same way, negative exponent means division. Negative exponent is the inverse of exponent.

So, whenever you find negative exponent, flip it down and then you can use it exactly like exponents or positive exponents.
Let us take up an example of what a negative exponent is.
Example: What is the value of (3)–4
Solution: ![]()
Example: What is the value of (–2)–5 ?
Solution: ![]()
Useful results for Exponents
Now let us take up some useful results for exponents that we can use to solve questions. These rules are essentially based on basic concepts and if you understand these rules, you go a long way in solving questions based on exponents.
Tooltip 1: Exponents in the case of negative numbers
You can represent exponents for negative numbers as:
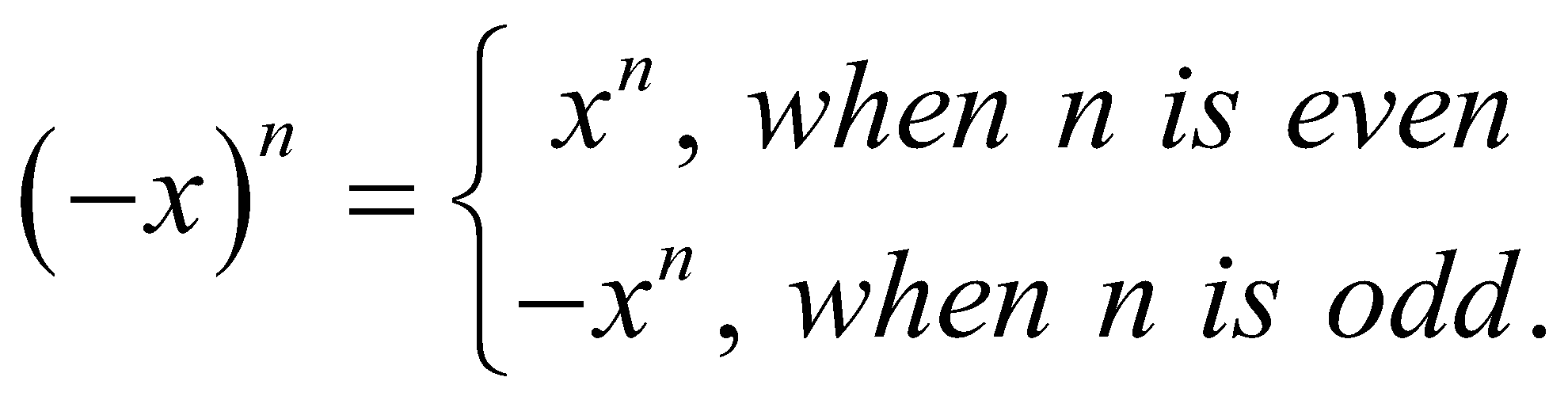
For example,
(i)![]()
(ii)![]()
Tooltip 2: Exponents for fractions
Let ![]() be any rational number and n be a positive integer. Then,
be any rational number and n be a positive integer. Then,
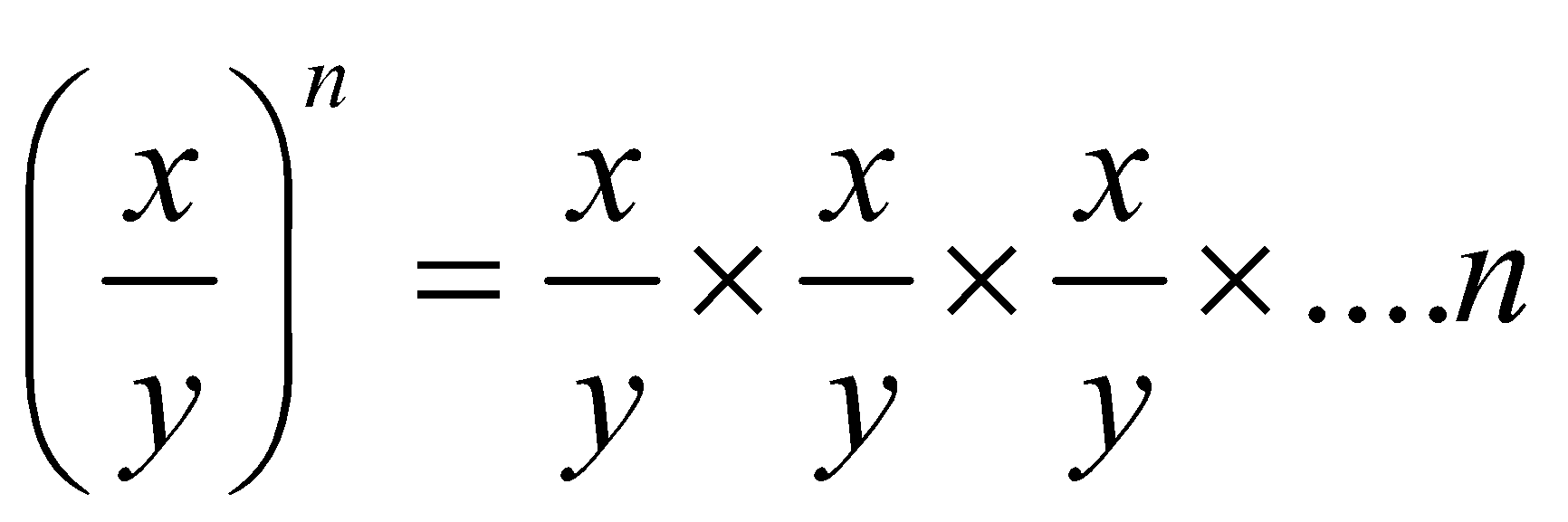 times =
times =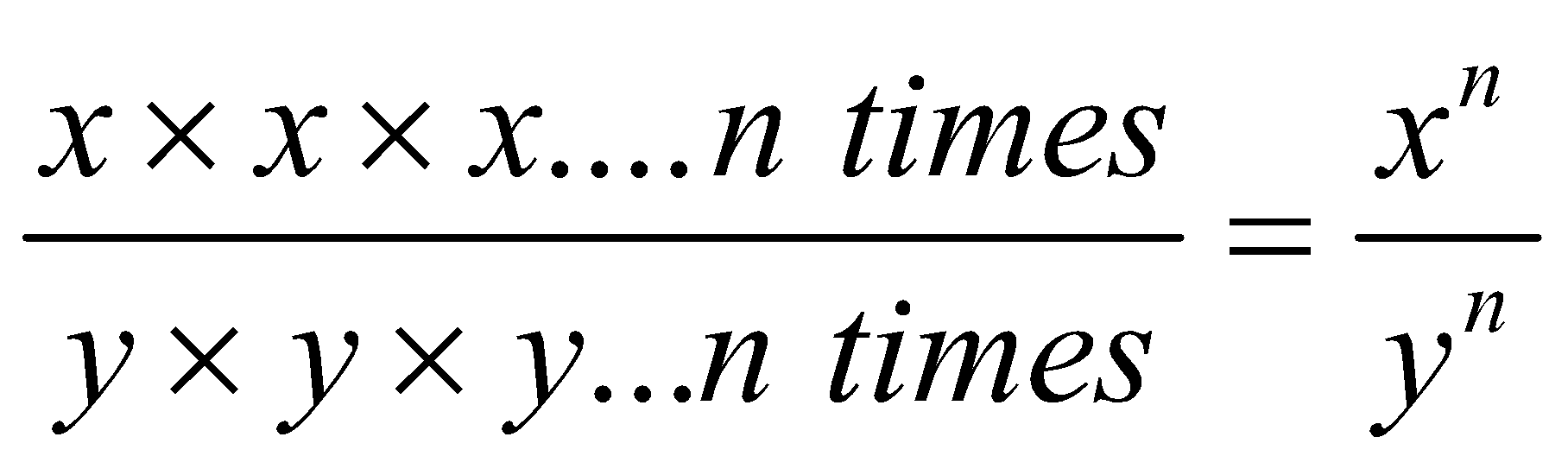 .
.
Thus, 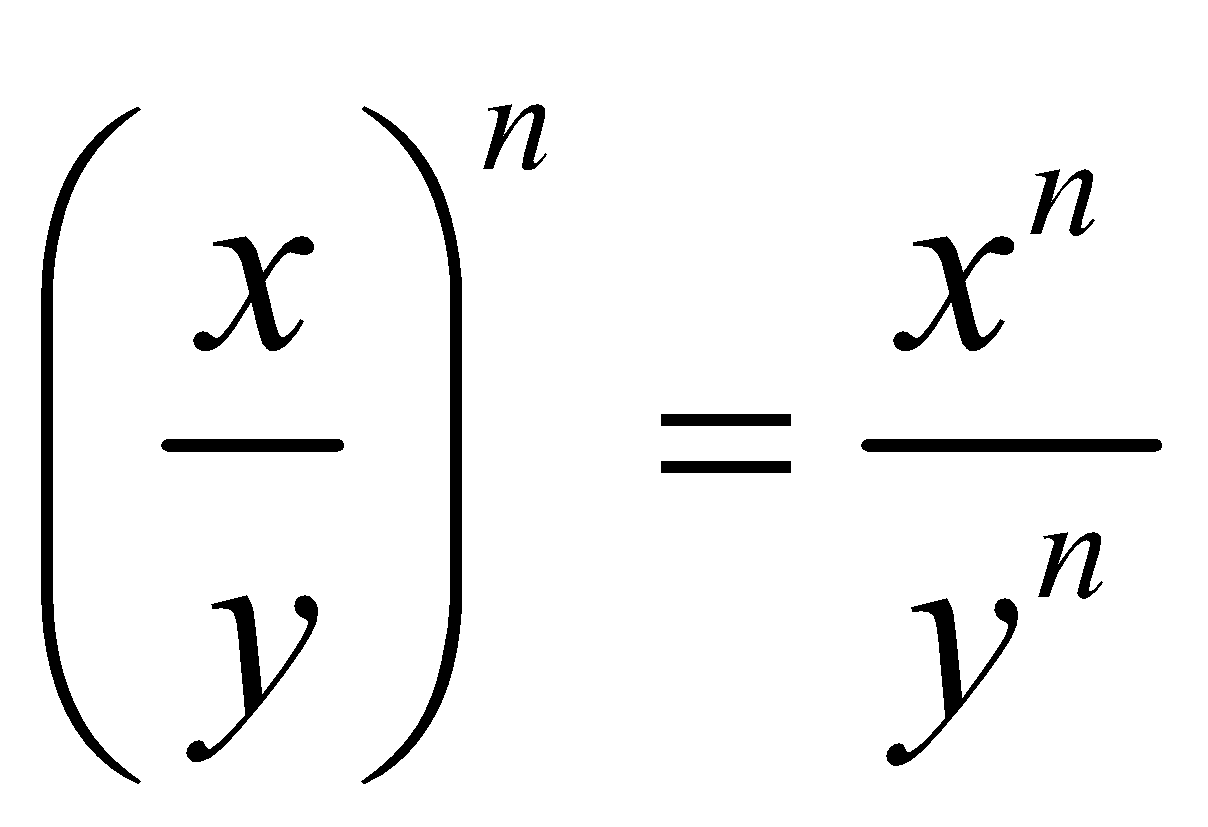 for every positive integer n.
for every positive integer n.
Example: Elaborate :- ![]()
Solution: We can write both numerator and denominator in product form separately.
![]() =
=![]()
Example: Write ![]() in exponent form.
in exponent form.
Solution: Count numbers in numerator and denominator and write them in their respective powers.
So![]()
Tooltip 3: Another rule for exponents related to fractions
Let ![]() be any rational number and n be a positive integer.
be any rational number and n be a positive integer.
Then, we define,![]() .
.
EXERCISE:
Question 1: Evaluate![]()
a. 4/25
b. 8/125
c. 8/25
d. 16/125
Solution: We know Hence, option (b)Answer and Explanation
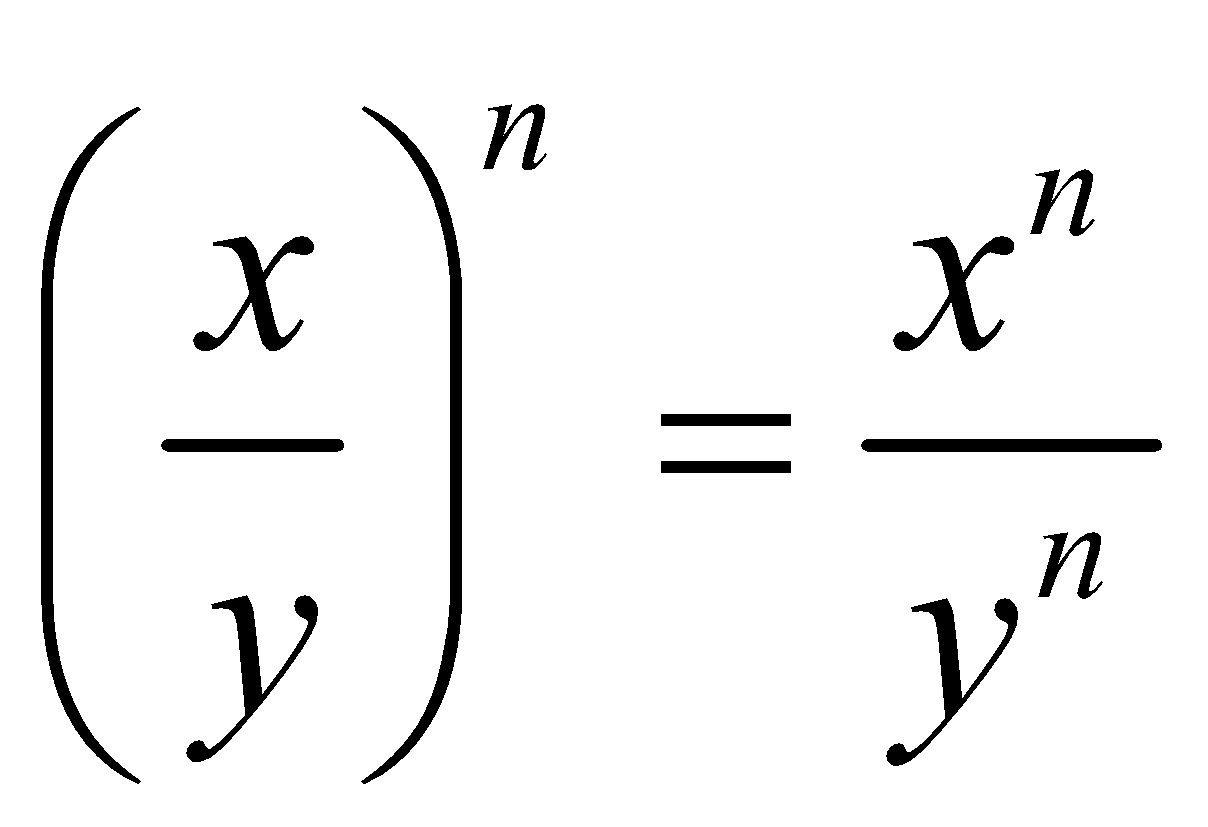
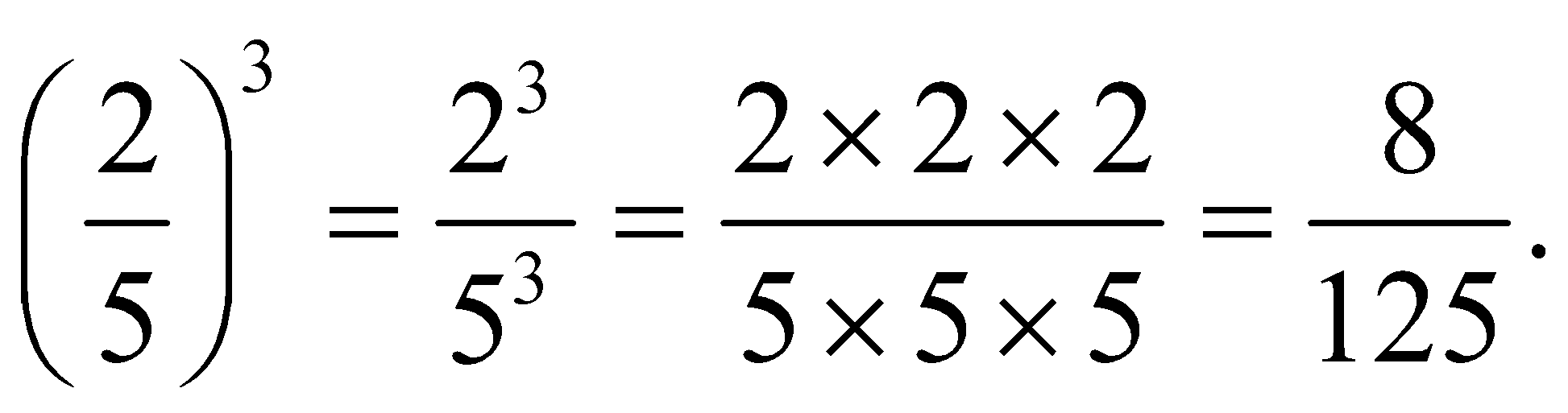
Question 2: Evaluate![]()
a. -27/125
b. 27/125
c. 27/625
d. -9/125
Answer and Explanation
Solution: We know
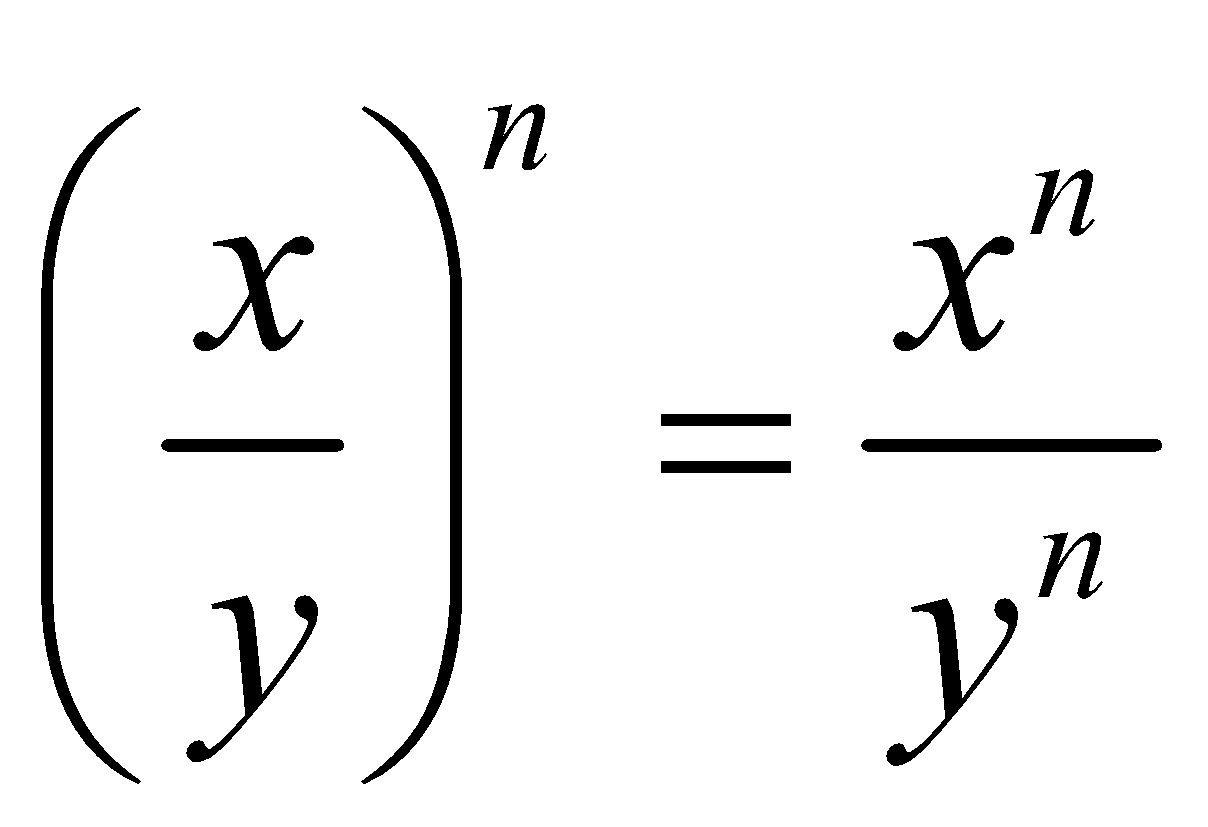
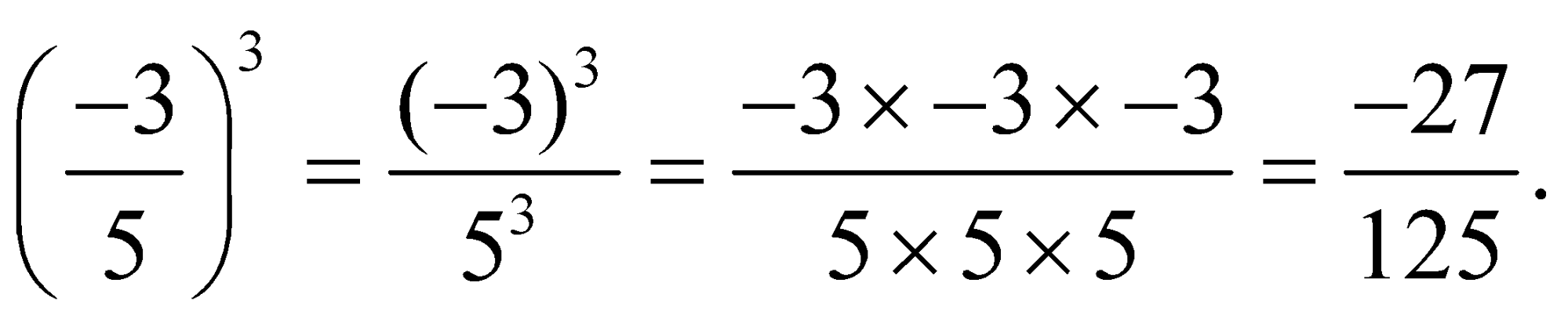
Hence, option (a)
Question 3: Evaluate
a. 125/27
b. 27/125
c. -125/27
d. -27/125
Answer and Explanation
Solution: We know
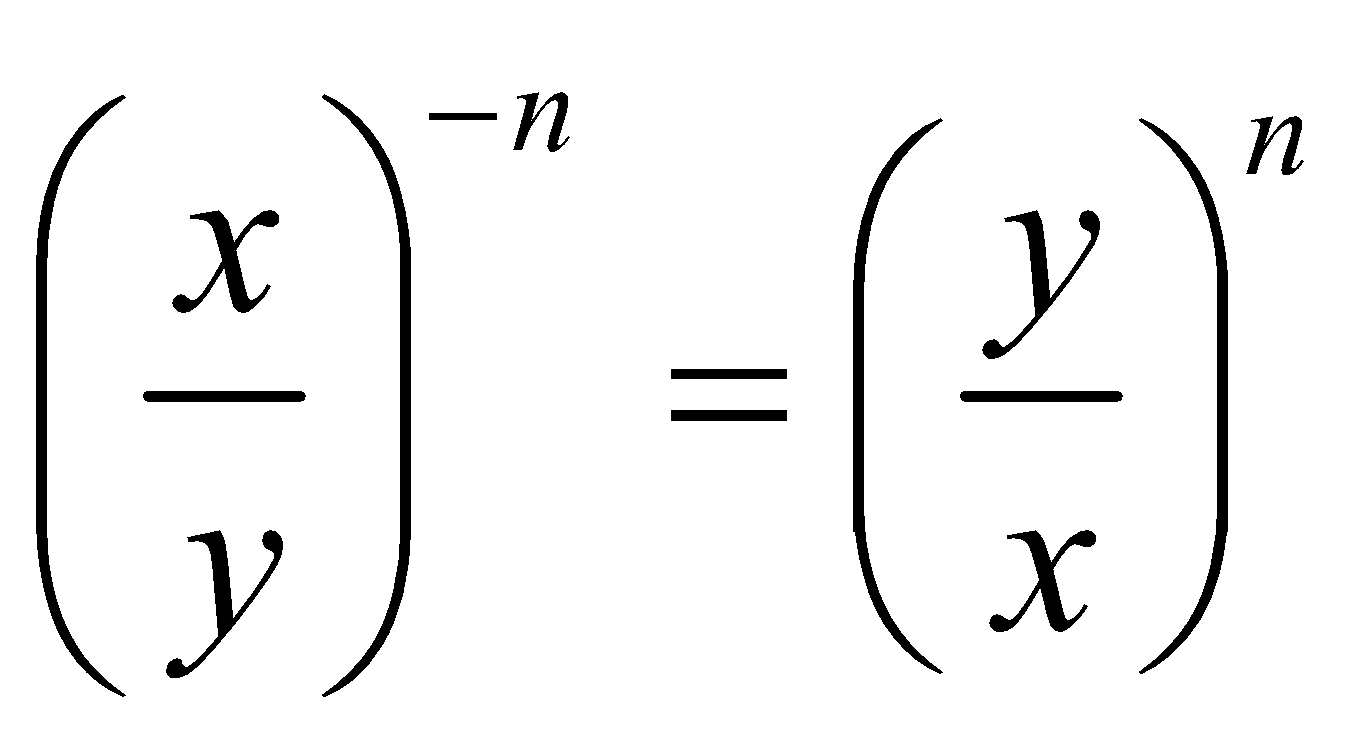
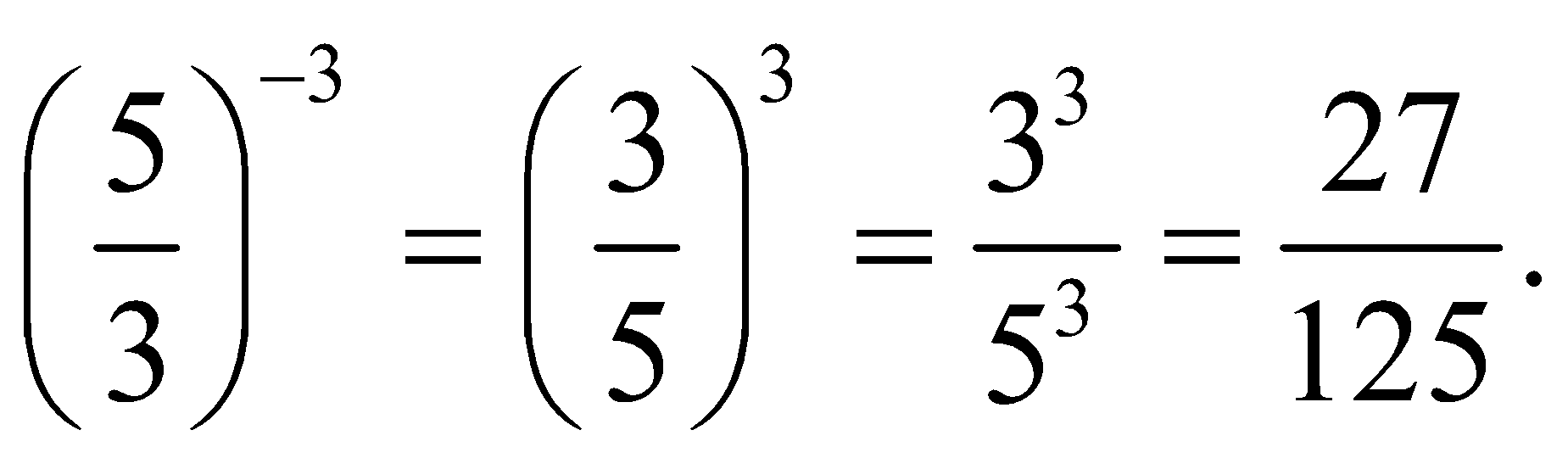
Hence, option (b)
Question 4: Evaluate 5-2
a. 25
b. -25
c. 1/25
d. -1/25
Answer and Explanation
Solution: It is an example of negative exponent
As 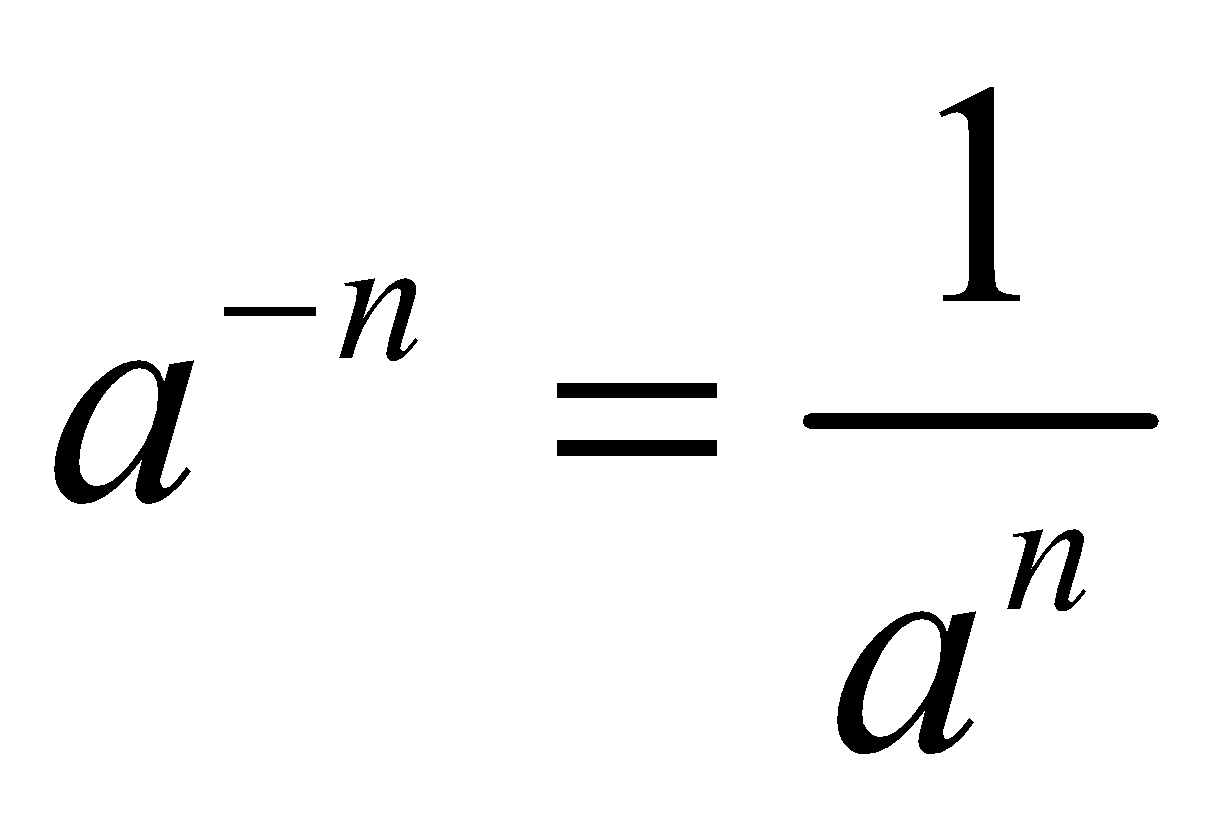
So ![]()
Hence, option (c)
Question 5: Evaluate
a. 1/25
b. -25
c. -1/25
d. 25
Answer and Explanation
Solution: We know

![]()
Hence, option (d)







