FACTORS

FACTORS

In this article, we will take the concept of factors further and learn about the sum of factors, and sum of even and odd factors. So, let’s get started.

 Sum of Factors:

Let us take an example to understand how to calculate the sum of factors.

Example: Find sum of factors of 12.

Solution:

Method 1:

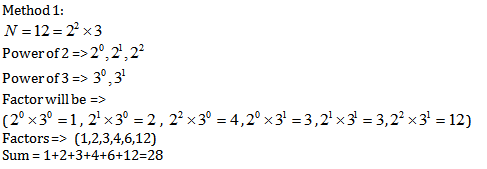
Method 2:

We can write above process as follows:

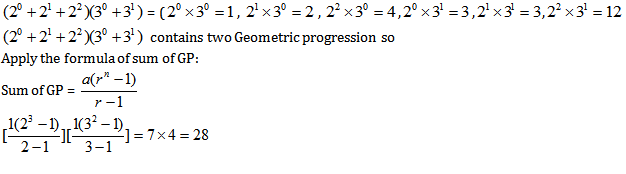
We can generalize the process and formula :

Sum Of Factors:

To find sum of factors of any number we will follow the following steps:

Step 1:  Write Prime factorization of given number i.e. convert the number in the form a^pb^qc^r where a,b,c are prime numbers and the p,q,r are natural numbers as their respective powers.

Step 2 : Sum of all the factors [(a^p+1-1)/(a-1) x (b^q+1-1)/(b-1) x (c^r+1-1)/(c-1)………]

Sum of Even Factors of a Number:

For this purpose we will exclude 2⁰

Example: Calculate sum of even factors of 72.

Solution: 

For even factors

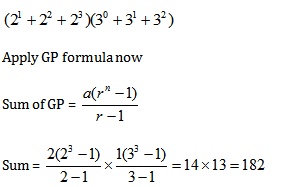
Sum of Odd Factors of a Number:

In this case only power of 2 which will be included is 2⁰

Example: Calculate sum of odd factors of 72.

Solution:

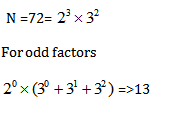
To get through the above concepts thoroughly, solve the exercise below:

 

EXERCISE:

Question 1.  Find the sum of all the factors of 600.

(1) 1860

(2) 3200

(3) 930

(4) 630

Question 2.  Find the sum of all the even factors of 600.

(1) 80

(2) 326

(3) 1736

(4) 124

 

Question 3.  Find the sum of all the odds factors of 600.

(1) 80

(2) 326

(3) 1736

(4) 124