FACTORS

In this article we’ll discuss an important concept related to factors i.e. Expressing a number as a product of 2 factors and ways to calculate the product of factors.

Expressing a Number as Product of Two Factors:

There can be the following 2 cases:

Case 1 :- when the number is not a perfect square

Case 2 :- when the number is  a perfect square

 Case 1 :- When The  Number Is Not A Perfect Square

 Method 1:

Step1:  Write Prime factor of given number i.e. convert the number in the form a^p b^q c^r

where a ,b, c are prime numbers and the p, q, r  are natural numbers as their respective powers.

Step 2: Find Number of factors which is ( p+1)(q+1)(r+1).

Step 3: Number of ways to express the number as a product of two numbers is exactly half its number of factors i.e.    ½ *(p+1)(q+1)(r+1).

 Let’s take an example on this :

 Example: In how many ways can you express 54 as a product of two of its factors?

Solution:

M1. Let us understand this logically first

Factors of 54 are 1, 2,3,6,9,18,27,54.

1 x54 = 54

2 x 27 = 54

3 x 18 = 54

6 x 9   = 54

By observation we can deduce that ways in which we can express 54 as product of its factor will be half of its total no of factors .

Method 2:  We will do the above problem step by step:

Step 1: Prime factors of 54 i.e. we write 54 = 2¹3³

Step 2: Number of factors of 54 will be (1+1)(3+1) = 2 x 4= 8

Step 3:  Hence number of ways to express 54 as a product of two numbers is exactly half its number of factors i.e. ½ *8 = 4 ways.

In fact we can list these 4 ways as well

Example: In how many ways you can express 120  as a product of two of its factors?

Solution:

Step 1: Prime factors of 120 i.e. we write 120  = 2³3¹5¹

Step 2: Number of factors of 120 will be (3+1)(1+1)(1+1) = 4 x 2 x2 = 16

Step 3:  Hence number of ways to express 120 as a product of two numbers is exactly half its number of factors i.e. ½ *16 = 8

Logically

Factors of 120 are 1,2,3,4,5,6,8,10,12,15,18,24,30,40,60,120.

So number of ways to express 120 as a product of two of its factors is

1×120 = 120

2 x 60 = 120

3 x 40 = 120

4 x 30 = 120

5 x 24 = 120

6 x 20 = 120

8 x 15 = 120

10 x12=120

 

Case 2 :- Perfect square as a product of two factors

In case of perfect square number we have odd number of factors i.e. the number of factors are odd. Hence, in that case required number of ways in which we can write perfect square number as a product of its two factors are:

Case 1 :-   if we do not include the square root of the number  :-  (n – 1)/2

Case 2 :-  if we include the square root of the number :- (n + 1 )/2

So number of ways to express a perfect square as product of two different factors (that means excluding its square root) is ½ {(p + 1)(q + I)(r + I) … – 1)}. And if we include the square root then required number is 1/2 {(p+1)(q+1)(r+1) … +1}

 Let’s take one example to understand this.

Example: In how many ways you can express 36 as the product of two of its factors?

Solution :

factors of 36 are 1,2,3,4,6,9,12,18,36

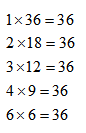
Step 1: Prime factors of 36 i.e. we write 36 = 2² x 3²

Step 2: Number of factors of 36 will be (2+1)(2+1)=9 (i.e. factors are 1,2,3,4,6,9,12,18,36)

Step 3: Since we are asked total number of ways hence we include square root of 36 i.e. 6 as well. Thus number of ways you can express 36 as the product of two of its factors is (9+1)/2=5

 

Finding Product of all the factors of a given number :-

Case 1 :- when the  number is not a perfect square

Case 2 :- when the  number is  a perfect square

 

Case 1 :- when the number is not a perfect square

To find product of all the factors we follow the following steps:

Step1: Prime factors N= a^p b^q c^r

Step2: total  Number of factors   (say X)

Step3: Product of all the factors is given by =  N^X/2

 

Let’s take an example on this :

 

Example: In how many ways can you express 54 as a product of all of its  factors?

Solution:

Method 1: Let us understand this logically first

Factors of 54 are 1, 2,3,6,9,18,27,54.

1 x 54 = 54

2 x 27 = 54

3 x 18 = 54

6 x 9   = 54

Method 2: Instead of multiplying all the numbers To calculate product of all the factors ,we will simply multiply

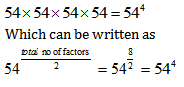
Case 2 :- when the  number is  a perfect square

To find product of all the factors we follow the following steps:

Step1: Prime factors N= a^p b^q c^r

Step2: total  Number of factors   (say X)

Step3: Product of all the factors is given by =

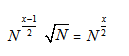
Example: In how many ways you can express 36 as the product of all of its factors?

Solution :

Method 1: factors of 36 are 1,2,3,4,6,9,12,18,36

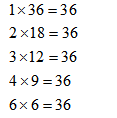
So product of all the factors =

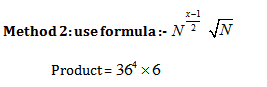
Note:

Expressing a number in multiplication of factors is same for both perfect and non perfect square numbers. The formula will be:

Product of all the factors is given by =  N^X/2

 

Number of co-primes of N which are less than N:

The number of numbers, which are less than N= p^a q^b r^c   (where p , q, r are prime numbers and the a,b,c are natural numbers as their respective powers)and are co-prime to N is given by:

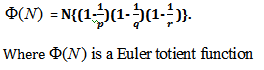
NOTE: In case of a prime number P ,all (P-1) number will be co-prime to it . we know that co-prime number are numbers which have no common factors . so in case of prime numbers except itself no other number have common factor with it .

 Example: How many numbers less than N= 500 are coprime to it?

Solution: Use formula

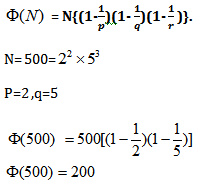
Example: How many numbers less than N= 13 are coprime to it?

Solution:

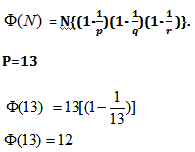
[1,2,3,4,5,6,7,8,9,10,11,12] all (p-1) that is (13-1=12) number will be coprime to 13 .

Product of two co-prime numbers:

To express the number as a product:

Step 1: Write Prime factorisation of given number i.e. convert the number in the form where p₁ ,p₂,p₃…..p_n are prime numbers and a,b,c….. are natural numbers as their respective powers.

Step 2: In the above step we have n prime numbers then the number of ways to express the number as the product of two co prime numbers =2^n-1

Because two primes are always co-prime and after we pick 1 prime the other prime can be picked in

2^n-1 ways.Hence number of ways in which we can write given number as a product of two co prime factors =2^n-1

 Example: In how many ways you can write 315 as product of two of its co-prime factors?
Solution:

Step 1: Prime factorization of 315 i.e. we write 315  = 3² x 5¹ x 7¹

Step2: In above number  3 prime numbers (3,5,7 )are used. Hence number of ways are 2^3-1 = 4.Infact we can mention these cases as well 9×35, 5 x 63, 7 x 45, 1*315.

 Pair of Factors that are Co-Prime to each other:

Let us understand the logic behind this with an example:

Example : How many pairs of factors of number 108 such that they are co-prime to each other?

Solution:

We know that 108 = 2²3³ let two factors are a and b, it is given that they are co-prime to each other.

Case (i) when a = 1, then b can take any factor of 108 so total (2+1)(3+1) such pairs exist.

Case (ii) when a = 2¹ then we have b = 3¹ or 3² or 3³ 3 such numbers

Case (iii) when a = 2² then we have b = 3¹ or 3² or 3³ 3 such numbers

Hence total such numbers is (2+1)(3+1) +2 ×3 = 12 + 6 = 18

Now let us generalize if number is in the form of N = a^pb^q

Let the above number has two factors as (A, B) and they are Co-prime to each other now to find such pairs let us see different cases: –

Case (i): When A = 1 then B can be any factor of number N hence total such values are (p + 1)(q + 1)

Case (ii): When A = a^x then B can take any value from 31, or 32 or ….. 3q for one value of ‘x’ there exist ‘q’ such values of B and number of possible values of ‘x’ is ‘p’ hence total such pairs are ‘pq’

Hence total number of such pairs are (p + 1)(q + 1)+ pq = 1+ (p + q) + 2pq

Let’s try another example.

 Example: How many pairs of factors of number 196 such that they are co-prime to each other?

Solution:

We know that 196 = 2² × 7² in this case we have only 2 prime factors hence number of such pairs is given by 1 +4 + 2 × 4 = 13 pairs.

If three prime factors then Number n = a^pb^qc^r

Let the above number has two factors as (A, B) and they are co-prime to each other now to find such pairs let us see different cases:

Case (i): When A = 1 then B can assume any value from all the factors of number n and total such values of B is (p + 1)(q+ 1)(r +1) = pqr + pq + pr + qr + 1

Case (ii): When A is in the form a^x (Total p such value of x exist) then B can assume any factor of number b^qc^r except 0, and total number of factors of b^qc^r except 1 is qr hence total such pairs  is ‘pqr’.

Similarly when A is in the form of b^y and c^z then also we will get ‘pqr’ such pairs. Hence total such pairs in this format is 3pqr.

Case (iii): When a is in the form of a^x (Total q such values of x exist) and B is in the form of b^y (y can assume q values) total such pairs are pq, similarly for the combination of a^x & c^z and b^y & c^z we will get pr and qr such pairs respectively. So total number of such pairs is pq + pr + qr

Hence total number of pairs is 1+ (p+q + r)+ 2(pq +pr + qr) + 4pqr.

EXERCISE:

Question 1.  In how many ways can you express 130 as a product of two of its factors?

(1) 8

(2) 4

(3) 16

(4) 24

Question 2. In how many ways you can express 144 as the product of two of its factors?

(1) 8

(2) 4

(3) 16

(4) 24

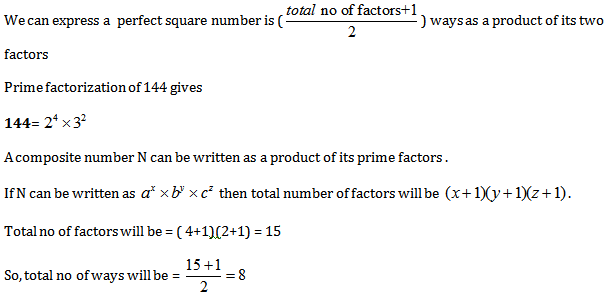
Question 3. How many numbers less than N= 29 are coprime to it .

(1) 28

(3) 24

(3) 26

(4) 34

 

Question 4. In how many ways you can write 500 as product of two of its co-prime factors?

(1) 8

(2) 4

(3) 2

(4) 6