FACTORS

When dealing with numbers, it happens so, that some numbers when added to themselves certain number of times result in a number which can be completely divided by both the original number and the second number. (Second number being the number of times of addition of original number)

So what are factors? Factors are the numbers that divide exactly into another number. In other words, we can say that when a number is divided by its factor there is no remainder left.

For example: Let us consider a number “ 12”. We can count manually that (1,2,3,4,6,12) can divide it (number 12). So 1,2,3,4,6,12 all are factors of 12.

Here, the number 12 was a small one. What if we have a big number?

Let’s see how to calculate factors:-

Example: Calculate factors of 48

Solution:

Step 1:- 1 and the number itself (48 in this case )will always be a factor .

Step 2:- next number is 2 , divide the number by 2 ; (48/2 =24 )

So 2 and 24 will be factors.

Step 3:- next number is 3 ,divide the number by 3 ;(48/3=16)

So 3 and 16 will be factors.

Step 4:- next number is 4 , divide the number by 4 ; (48/4=12)

So 4 and 12 will be factors.

Step 5:- next number is 5 , but it cannot divide 4 8 completely. So move on to next number that is 6.

Divide 48 by 6 (48/6=8). So 6 and 8 will be factors.

Next number will be 7 but it cannot divide 48. Moving on to next number, 8 can be a factor that we already have paired up with 6. So we will stop here.

So ( 1,2,3,4,6,8,12,16,24,48) are the required factors .

Prime factors: We have studied in earlier chapters that natural numbers are of two type :

Prime
Composite

Composite numbers are made of prime numbers. We can multiply any two or more prime numbers and get composite numbers. So every composite number will have a unique set of prime numbers and those prime numbers that are used in composite numbers are called prime factors.

Let us understand this more.

Take an example of number 12 again. We can divide 12 into its prime factors.

So, 2 and 3 are the prime factors of 12.

Calculating Prime factors.

Example: Calculate prime factors of 432.

Solution:

Step 1:- Check for the smallest prime number which can divide the given number.

The number 432 has even unit digits. So 2 will divide it. Write the quotient below it .

Step 2 :- Check for the smallest prime number which can divide this quotient. In this case 2 can divide it completely. So repeat the previous process .

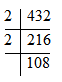
Keep repeating the process.

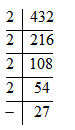
Now we now 2 cannot divide 27. So we need to look for slightly bigger prime number than 2. Check for prime number 3.

Sum of digits of 27 = 2+7= 9; 9 is divisible by 3 so 27 will also be divisible by 3 .

Now repeat the previous process.

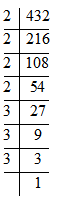
Prime factors of 432 will be 2 and 3.

Example: Calculate the prime factors of 1029.

Solution:

Step 1 :- check for the smallest prime number which can divide the given number. 2 cannot divide 1029 as unit digit is not even.

Sum of digits of 1029 will be 1+0+2+9=12

Which is divisible by 3.

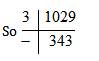
Now 343 is not divisible by 3 so look for another prime number. After 3, the next prime number is 5 that cannot divide 343. So look out for next prime number, which is 7.

343 is divisible by 7.

{Divisibility test. Seed number for 7 is -2, so multiply unit digit with -2 and add .

34 +(-6)=28; which is divisible by 7 . }