The concept of fractions, though a simple one, can often cause some confusions. Having not solved sufficient questions based on this simple concept, students often tend to confuse the problems. Considering the basic nature of this topic, it is important we go through the basic concepts so that you are not caught on the wrong foot while solving questions.
So what are Fractions?
Definition
Technically, a fraction is defined as part of the whole. The most common example of a fraction that comes to mind is half. When we say give me half of something, we are essentially demanding ½ part of it, in other words, ½ is the fractional representation for half.
Fractions are nothing else but the numerator divided by denominator, i.e. they occur in the form X/Y where X is the numerator and Y is the non-zero denominator.
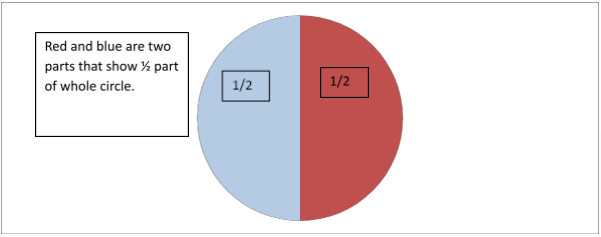
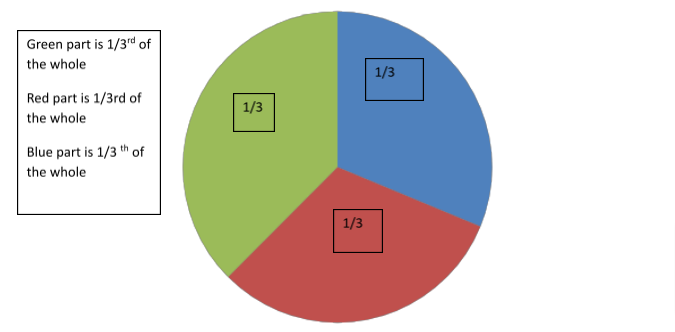
So what does the numerator and denominator in a fraction signify?
The numerator represents how many parts of that whole are being considered. To remember simply, numerator is the top number of the fraction that represents the numbers of parts that are to be chosen.
The denominator represents the total number of parts created from the whole. In other words, it is the bottom number representing the total number of parts created.
Example of Fractions: ½, 2/3, 3/4, are the numbers which are in the form of x/y, where y has to be a non-zero number.
Types of Fractions:
Proper Fraction: When Numerator of the fraction is less than the Denominator, then the fraction is called as proper fraction.
For example: 2/3, 4/5, 6/7, etc
Improper fraction: When Numerator of the fraction is more than Denominator, then the fraction is called as improper fraction. For example: 5/3, 7/5, 19/7, etc
Mixed fraction: When a natural number combines with a fraction, that fraction is called a mixed fraction.
For Example: 21/2 ,34/5 ,etc. In other words, the mixed fractions are improper fractions.
Properties of fractions
Let us explore some useful properties of fractions that you can use to solve questions.
Property 1: If we multiply the numerator and denominator by same quantity, the basic value of fraction will never change.
For example: 4/5 x 5/5 = 20/25 = 4/5
Property 2: If there are two fractions a/b and c/d then a/b=c/d when ad=bc.
For example,3/4 = 12/16 because 3 x 16 = 4 x 12
Property 3: A fraction with zero as the denominator is not defined.
Property 4: If the numerator of the fraction is zero, then the fraction equals to zero.
Property 5: If the numerator and denominator of the fraction are equal, then the fraction is equal to one.
Applications of Fractions
Given below are some of the basic applications of fractions:
- Fraction helps us determine the part of any number
¾ part of 56 = ¾ x 56 = 42
4/5 part of 90 = 4/5 x 90 =72
- You can be asked to represent a number in the form of fraction.
For example, you can be asked to represent 15 as a fraction of 450.
This can be done as follows:
15/450 = 1/30
In the above example, it can be easily seen that 15 is our numerator and 450 is our denominator
- Always remember that the major quantity from which we have to extract something is the denominator.
For example, when we say 4/5, we are essentially extracting four parts out of five.
- Extending the above concept, the quantity that is extracted is our numerator
For example: 15/450 = 1/30
15 is the numerator because we have extracted 15 from 450 and the denominator is 450 because 15 is extracted from 450. So, we can say that 1/30th part of 450 is 15.
- Converting percentages into equivalent fractions makes our calculation easy.
For example:
If you remember 37.5% = ![]() and you are asked to find 37.5% of 24 then you can write
and you are asked to find 37.5% of 24 then you can write
37.5% of 24 =![]() X24 = 9
X24 = 9
Remember the following equivalent fractions for given percentages:
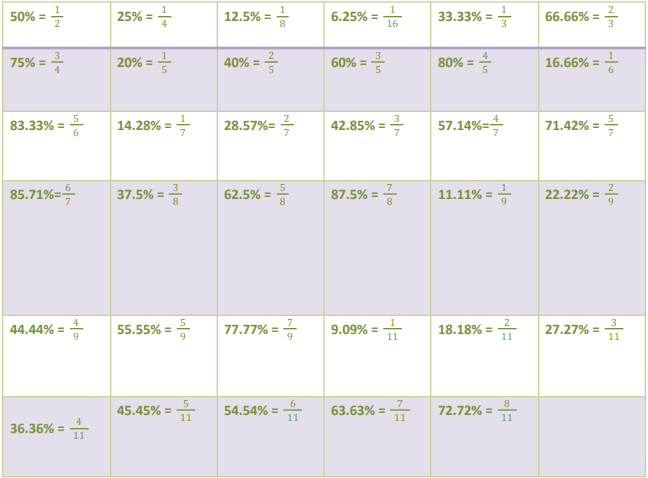
This percentage to fraction conversion and vice-versa has a huge application in DI sets. Therefore, make sure that you are thorough with this table.













