Geometry and Mensuration: Level 3 Test 5

This is an assessment test.
To draw maximum benefit, study the concepts for the topic concerned.
Kindly take the tests in this series with a pre-defined schedule.

Geometry and Mensuration: Level 3 Test 5

Please wait while the activity loads.
If this activity does not load, try refreshing your browser. Also, this page requires javascript. Please visit using a browser with javascript enabled.

If loading fails, click here to try again

Congratulations - you have completed Geometry and Mensuration: Level 3 Test 5.You scored %%SCORE%% out of %%TOTAL%%.You correct answer percentage: %%PERCENTAGE%% .Your performance has been rated as %%RATING%%

Your answers are highlighted below.

Question 1

AB is the diameter of the given circle, while points C and D lie on the circumference as shown. If AB is 15 cm, AC is 12 cm and BD is 9 cm, find the area of quadrilateral ACBD.

A	54p sq. cm
B	216p sq. cm
C	162p sq. cm
D	None of these

Question 1 Explanation:

ACB and ADB are inscribed in a semicircle and
thus angle ACB and angle ADB = 90^o
Thus by Pythagoras theorem,
BC and AD = 9 and 12 respectively.
Thus the area of ACBD = ½ x 2 x 9 x 12 = 108
Thus correct option is (d)

Question 2

The sum of the areas of two circles, which touch each other externally, is 153π units. If the sum of their radii is 15 units, find the ratio of the larger to the smaller radius.

A	4 : 1
B	2 : 1
C	3 : 1
D	None of these

Question 2 Explanation:

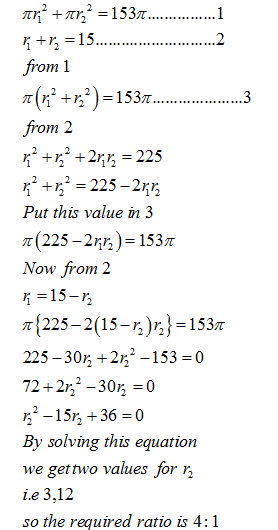
Question 3

In a rectangle, the difference between the sum of the adjacent sides and the diagonal is half the length of longer side. What is the ratio of the shorter to the longer side?

A	13:2
B	1: 13
C	2: 5
D	3: 4

Question 3 Explanation:

$ \displaystyle \begin{array}{l}Let\text{ }the\text{ }two\text{ }sides\text{ }be\text{ }x\text{ }and\text{ }y\text{ }and\text{ }y>xThus,\\x+y-\sqrt{{{x}^{2}}+{{y}^{2}}}=\frac{1}{2}x\\=>\frac{x}{y}+y=\sqrt{{{x}^{2}}+{{y}^{2}}}\\=>\frac{{{x}^{2}}}{4}+{{y}^{2}}+\frac{2xy}{2}={{x}^{2}}+{{y}^{2}}\\=>\frac{3x}{4}=y\\=>y:x=4:3\end{array}$

Question 4

Four identical coins are placed in a square. For each coin, the ratio of area to circumference is same as the ratio of circumference to area. Then, find the area of the square that is not covered by the coins.

A	16(Π-1)
B	16(16Π-1)
C	16(4-Π)
D	16(4 – Π/2)

Question 4 Explanation:

Now considering the rule given one can find out the radius of each circle to be 2 units.
Taking one small square left out area = 4²-Πx2²=16 - 4Π
Now there are 4 such squares .
Thus total area = 4(16 - 4Π)
= 16(4-Π)

Question 5

Consider a circle with unit radius. There are seven adjacent sectors, S1, S2, S3, …., S7 , in the circle such that their total area is 1/8 of the area of the circle. Further, the area of the jth sector is twice that of the (j - 1)^th sector, for j = 2, .....,7 What is the angle, in radians, subtended by the arc of 51 at the centre of the circle?

A	$ \displaystyle \frac{\pi }{508}$
B	$ \displaystyle \frac{\pi }{2040}$
C	$ \displaystyle \frac{\pi }{1016}$
D	$ \displaystyle \frac{\pi }{1524}$

Question 5 Explanation:

Let the area of S1 be a
Thus the total area =(2⁷– 1)a = 127a
The total angle = 127a x 8 = 1016a
Thus the angle of sector S1 = Π/1016
Correct option is (a)

Once you are finished, click the button below. Any items you have not completed will be marked incorrect. Get Results

There are 5 questions to complete.

←

List

→

Return

Shaded items are complete.