- This is an assessment test.
- These tests focus on geometry and mensuration and are meant to indicate your preparation level for the subject.
- Kindly take the tests in this series with a pre-defined schedule.
Geometry and Mensuration: Test 24
Congratulations - you have completed Geometry and Mensuration: Test 24.You scored %%SCORE%% out of %%TOTAL%%.You correct answer percentage: %%PERCENTAGE%% .Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
AB, EF and CD are parallel lines. Given that, EF= 5 cm GC = 10 cm, AB = 15 cm and DC = 18 cm. What is the value of AC?
20 cm | |
24 cm | |
25 cm | |
28 cm |
Question 1 Explanation:
$ \begin{array}{l}\because AB||EF||CD\\\frac{EF}{CD}=\frac{EG}{GC}\\=>\frac{EF}{18}=\frac{5}{10}\\=>EF=9\\In\vartriangle ABC\text{ }and\vartriangle EFC\text{ }\left( similar\text{ }triangles \right),\\\frac{EF}{AB}=\frac{EC}{AC}\\=>9/15=15/AC\\AC=(15\times 15)/9=25cm\end{array}$
Question 2 |
In the given triangle, AB is parallel to PQ. AP = c, PC = b, PQ = a, AB = x. What is the value of x?
$ \displaystyle a+\frac{ab}{c}$ | |
$ \displaystyle a+\frac{bc}{a}$ | |
$ \displaystyle b+\frac{ca}{b}$ | |
$ \displaystyle a+\frac{ac}{b}$ |
Question 2 Explanation:
$ \begin{array}{l}~ABC\text{ }is\text{ }congruent\text{ }to~PQC,\\\frac{AC}{PC}=\frac{BC}{QC}=\frac{AB}{PQ}\\=>x=\frac{AC\times PQ}{PC}=\frac{(b+c)a}{b}=a+\frac{ac}{b}\end{array}$
Question 3 |
In the given figure, QR is parallel to AB, DR is parallel to QB. What is the number of distinct pairs of similar triangles?
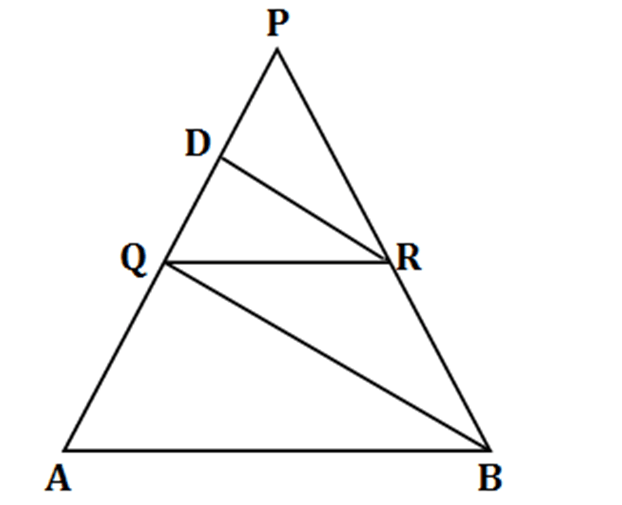
1 | |
2 | |
3 | |
4 |
Question 3 Explanation:
$ \displaystyle \begin{array}{l}The\text{ }triangles\vartriangle PDR\text{ }and\vartriangle PQB,\vartriangle PQR\text{ }and\vartriangle PAB,\vartriangle DRQ\text{ }and\vartriangle QBA\text{ }are\text{ }similar.\\Thus\text{ }there\text{ }are\text{ }three\text{ }possible\text{ }pairs\text{ }of\text{ }triangles.\\Correct\text{ }option\text{ }is\text{ }\left( c \right).\end{array}$
Question 4 |
If the angels of a triangle are 30°, 60° and 90°, then what is the ratio of the corresponding sides?
1: 2: 3 | |
1: 1: √2 | |
1: √3: 2 | |
1: √2: 2 |
Question 4 Explanation:
$\begin{array}{l}\tan \,60=\sqrt{3}\\Thus\text{ }the\text{ }ratio\text{ }of\text{ }corresponding\text{ }sides\text{ }=1:\text{ }\surd 3:\text{ }2\\\end{array}$
Question 5 |
I is the incentre of ∆ABC, ABC= 60o and ACB= 50o. The BIC is:
55o | |
125o | |
70o | |
65o |
Question 5 Explanation:
$ \displaystyle \begin{array}{l}\angle BIC\text{ }=~=\text{ }180\text{ }\frac{1}{2}\left( ABC+ACB \right)\\\text{=180 - }30-25\text{ }=\text{ }125.\\Correct\text{ }option\text{ }is\text{ }\left( b \right)\end{array}$
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 5 questions to complete.
List |
