- This is an assessment test.
- These tests focus on geometry and mensuration and are meant to indicate your preparation level for the subject.
- Kindly take the tests in this series with a pre-defined schedule.
Geometry and Mensuration: Test 3
Congratulations - you have completed Geometry and Mensuration: Test 3.You scored %%SCORE%% out of %%TOTAL%%.You correct answer percentage: %%PERCENTAGE%% .Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
A cylindrical container of height 14 m and base diameter 12 m contains oil. This oil is to be transferred to one cylindrical can, one conical can and a spherical can. The base radius of all the containers is same. The height of the conical can is 6 m. While pouring some oil is dropped and hence only 3/4m of cylindrical can could be filled. How much oil is dropped?
54π m3 | |
36π m3 | |
46π m3 | |
50π m3 |
Question 1 Explanation:
Total volume of the cylinder

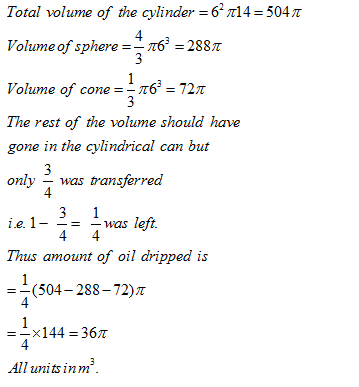
Question 2 |
The length of a rectangle is increased to 3/2 times of its length and breadth is reduced to 1/ 3rd of its breadth. What is the change in area?
1/3 | |
1/4 | |
1/2 | |
No change |
Question 2 Explanation:
Let the original length and breadth are 'a' and 'b' respectively. The new length and breadth are 3a/2 and b/3
The change in area = {ab –( 3a/2 x b/3)}
= { ab – ab/2}
= ab/2
Hence the new area is half of the original area. Correct option is (c).
The change in area = {ab –( 3a/2 x b/3)}
= { ab – ab/2}
= ab/2
Hence the new area is half of the original area. Correct option is (c).
Question 3 |
The ratio of the volume of a cube to that of the sphere which can fit inside the cube is
3: 4 | |
21: 11 | |
11: 22 | |
4: 3 |
Question 3 Explanation:
Let the side of the cube is '2x' units, so its volume is 8x3.
Now if the sphere fits inside the cube, then the diameter of the sphere will be same as the side of the cube.
So the radius of the sphere is x units and its volume is (4/3)(22/7)( x3) = (88x3/21)
Hence the required ratio is
8x3 : (88x3/21) = 21: 11
Now if the sphere fits inside the cube, then the diameter of the sphere will be same as the side of the cube.
So the radius of the sphere is x units and its volume is (4/3)(22/7)( x3) = (88x3/21)
Hence the required ratio is
8x3 : (88x3/21) = 21: 11
Question 4 |
In measuring the sides of a rectangular plot, one side is taken 5% in excess and the other 6% in deficit. The error per cent in area calculated of the plot is
=1% | |
1.3% | |
1.5% | |
3% |
Question 4 Explanation:
Area of new rectangle = 1.05 X .94 = 0.987.
Approximate decrease is (100-98.7) = 1.3 %
Correct option is (b)
Approximate decrease is (100-98.7) = 1.3 %
Correct option is (b)
Question 5 |
The circumference of a circle is equal to the side of a square whose area measures 407044 sq. cms. What is the area of the circle?
22583.2 sq. cms. | |
32378.5 sq. cms. | |
41263.5 sq. cms. | |
39483.4 sq. cms. |
Question 5 Explanation:
Let the side of the square is 'a' units. So we have a2 = 407044
=>a = 638 cm
Let the radius of the circle is 'r'. So 2πr = 638
r = 638/2π
The area of the circle = πr2 = π(638/2 π)2 = {(638 x 638 x 7)/(4 x 22)} = 32378.5cm2
=>a = 638 cm
Let the radius of the circle is 'r'. So 2πr = 638
r = 638/2π
The area of the circle = πr2 = π(638/2 π)2 = {(638 x 638 x 7)/(4 x 22)} = 32378.5cm2
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 5 questions to complete.
List |






