A number has limited number of factors unlike multiples, so out of these factors what is an HCF?
As the name suggests, HCF is the highest common factor of two or more numbers. In other words, HCF is the biggest number that can divide all the given numbers.
METHODS TO FIND HCF
There are two methods to find HCF / GCD:-
- Prime factorization method
- Long division method
Let’s discuss these methods in detail.
- Prime factorization method:
Step 1: write prime factors of given numbers.
Step 2: HCF will be product of least common power of prime number present between / among given numbers.
Let’s understand it with the help of an example.
Example: What is the HCF of 18 and 36?
A.18
B.9
C.12
D.36
Answer: Option A
Explanation:
Step 1 :-
18= 2 x 3 x 3 = 21 x 32
36 = 2 x 2 x 3 x 3 = 22 x 32
Step 2 :- least power of 2 is 1 and of 3 is 2
Hence 2 x 32 = 18 is required HCF.
You’ll find more questions to practice this method at the end of this article.
- HCF by Long Division Method
To find the H.C.F. of the given number using long division method, we will follow the following steps:
- We divide the bigger number by smaller one.
- Divide smaller number of step 1 with remainder obtained in step 1.
- Divide divisor of second step with remainder obtained in step 2.
- We will continue this process till we get remainder zero and divisor obtained in end is the required H.C.F.
Example: Find the HCF of 288 and 600
Solution:
Follow the steps as follows:

Hence required HCF is 24.
Let’s practice these concepts solving the exercise below.
EXERCISE:
Question 1. What is the HCF of 12, 18 and 30?
A. 10
B. 5
C. 6
D. 8
Answer and Explanation
Answer: Option C
Explanation:
12 = 2 x 2 x 3 =22 × 31
18 = 2 x 3 x 3 = 21 x 32
30 =2 x 3 x 5=21 x 31 x 51
Primes involved are 2, 3 and 5 minimum powers involved are 1 ,1 and 0 respectively. Hence
21 x 31 x 50 = 6 is required HCF.
Question 2. Find HCF of 3360, 2240 and 5600.
A. 1000
B. 1120
C. 1630
D. 1210
Answer and Explanation
Answer: Option B
Explanation:
HCF of 3360, 2240 and 5600

Question 3 . Find HCF of 304 and 323.
A. 19
B. 50
C. 57
D. 80
Answer and Explanation
Answer: Option A
Explanation:
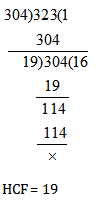
Question 4. Find HCF of 3015 and 5040 by long division method.
A. 40
B. 50
C. 45
D. 55
Answer and Explanation
Answer: Option C
Explanation:
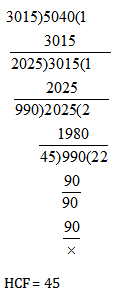
Question 5. Find HCF of 1651 and 2032 by prime factorization method.
A.197
B.150
C.128
D.127
Answer and Explanation
Answer: Option D
Explanation:
1651 = 13 × 127
2032 = 16 × 12
HCF = 127







