For the concept of identifying the unit digit, we have to first familiarize with the concept of cyclicity. Cyclicity of any number is about the last digit and how they appear in a certain defined manner. Let’s take an example to clear this thing:
The cyclicity chart of 2 is:
21 =2
22 =4
23 =8
24=16
25=32
Have a close look at the above. You would see that as 2 is multiplied every-time with its own self, the last digit changes. On the 4th multiplication, 25 has the same unit digit as 21. This shows us the cyclicity of 2 is 4, that is after every fourth multiplication, the unit digit will be two.
Cyclicity table:
The cyclicity table for numbers is given as below:
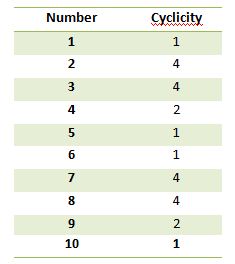
How did we figure out the above? Multiply and see for yourself. It’s good practice.
Now let us use the concept of cyclicity to calculate the Unit digit of a number.
What is the unit digit of the expression 4993?
Now we have two methods to solve this but we choose the best way to solve it i.e. through cyclicity
We know the cyclicity of 4 is 2
Have a look:
41 =4
42 =16
43 =64
44 =256
From above it is clear that the cyclicity of 4 is 2. Now with the cyclicity number i.e. with 2 divide the given power i.e. 993 by 2 what will be the remainder the remainder will be 1 so the answer when 4 raised to the power one is 4.So the unit digit in this case is 4.
For checking whether you have learned the topic, think of any number like this, calculate its unit digit and then check it with the help of a calculator.
Note : If the remainder becomes zero in any case then the unit digit will be the last digit of acyclicity number
where a is the given number and cyclicity number is shown in above figure.
Lets solve another example:
The digit in the unit place of the number 7295 X 3158 is
A. 7
B. 2
C. 6
D. 4
Solution
The Cyclicity table for 7 is as follows:
71 =7
72 =49
73 = 343
74 = 2401
Let’s divide 295 by 4 and the remainder is 3.
Thus, the last digit of 7295 is equal to the last digit of 73 i.e. 3.
The Cyclicity table for 3 is as follows:
31 =3
32 =9
33 = 27
34 = 81
35 = 243
Let’s divide 158 by 4, the remainder is 2. Hence the last digit will be 9.
Therefore, unit’s digit of (7925 X 3158) is unit’s digit of product of digit at unit’s place of 7925 and 3158 = 3 * 9 = 27. Hence option 1 is the answer.






Very easy explanation. Thank you
Very nice explanation. Thank you so much.
thank you very much sir and its very simple and easy it is also very useful to me sir.
Thankyou. I had been looking for an answer to this type of questions
Thank you so much..it is very understandable and easy to learn..
Its really helpful for the students who are just started solving Aptitude Numbers Questions like me….
Thanks a lot
The way you have explained this has the effect of leaving no ambiguity in the minds of people concerned. I would like to thank the author for their efforts, for, this was the only place where I was able to understand it in its fullest terms.
pls solve unit digit of 27^37^35.
Thanks it is very useful for future
It’s simple and helpful for aptitude tests
Thankyou it is very useful
157^123 what is the unit
Unit digit of 157^123 is same as the unit digit of 7^123. Now the cycle of 7 is of 4 steps. Divide 123 by 4 you get 3 as remainder. So the unit digit will be same as 7^3 = 343 or 3.
tell me what is the numbers which come on unit digit of square number
Divyansh, Can you post your doubt more specifically…
Thank u very much for this easy and simple to find units digit
thanks for your explanation ..
for example 0 is the remainder but 4 power of 0 is not there .my question is 4^44 .we got the remainder 0 so we 4^0=1 but 1 is not a correct answer .
please explain the answer.
Sir in case of zero remainder,the unit digit will be the last digit of 4^cyclicity number
As the cyclicity of 4 is 2 therefore the in case of zero remainder the unit digit will be 6 not 4^0 =1
for example
4^2 = last digit is 6
4^4 = last digit is 6
4^6 = last digit is 6
this topic is very useful for all students
what willbe the answer of 2^4 with ur logic i will get 2 thats wrong answer will be 6
The answer will be 6
When we divide 4 with the cyclicity number i.e 4 ,the remainder will be zero
and in case of remainder zero the last digit of the number will be last digit of 2^cyclicity number
Now the cyclicity number of 2 is 4
Therefore the unit digit of 2^4 is 6
The last cyclicity of 4 is 4^2 .
the value of 4^102 is supposed to have 6 at the unit place.Calculating by your method..4 has a cyclicity of 2. Dividing 102 by 2, we get remainder as zero. 4^0=1. Buh!
The answer is 6
In case of zero remainder the unit digit will be the last digit of a^cyclicity number
Here the value of a is 4 and the value of cyclicity number is 2
Hence the last digit of 4^102 will be 6
To every power we have to divide it by 4 only. The one given is absolutely wrong.
But yes its given that in case of 0 remainder we have take the unit digit of the last cyclicity number i.e, 4^2.
Very nice .Its a short and quick method.