When dealing with the division of numbers, it is certain that the number to be divided is not always a factor the number with which it is divided. This brings remainders into existence. So what are remainders? In this article, we are going to study about them and it will help you know the very basic of remainders. Also, you’ll learn about the approach to solve questions on remainders.
Basic Concept:
When A number N (dividend) is divided by a number D (divisor), it gives a Q (quotient) and R (remainder).
For example:
![]()
Dividend = 7 ; Divisor = 3 ; quotient = 2 ; Remainder = 1
If a number is completely divisible by another number then the remainder is zero.
For example :-
![]()
Dividend = 6 ; Divisor = 3 ; quotient = 2 ; Remainder = 0
We can generalize this relationship among these four variables :-
Dividend = divisor * quotient + remainder
N = D*Q+R
Let us apply this relation to some word problems.
Example: If 6 chocolates are given to a group of 24 children. How many chocolates each child will receive?
Solution: 
There is no remainder left.
N=24; D= 6 ; Q=4 ; R=0
It can be written in the form of equation like this
24=6*4+0
Tooltip 1:
Remainders can be obtained by splitting a number N into two or more than two parts
![]()
remainders can be added later.
This property really comes in handy in calculating remainder of a very big number.
DERIVATION:
Let us split a number N into two numbers N1 and N2 that give remainders R1 and R2 when divided by D. We can show the result as follows –
N1 = Q1D + R1 and N2 = Q2D + R2
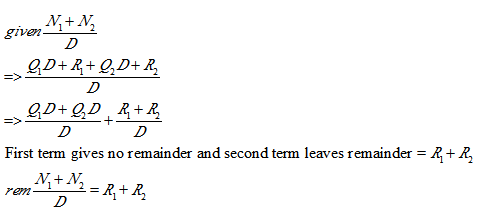
Example: What is the remainder when 15651 is divided by 100?
Solution: 15651 can be written as: – 15000+600+51
Dividing it by 100

Tooltip 2:
Remainders can be obtained by splitting a number N into two or more than two parts
![]()
Respective remainders can be multiplied later .
DERIVATION:
Let us split a number N into two numbers N1 and N2 that give remainders R1 and R2 when divided by D. We can show the result as follows –
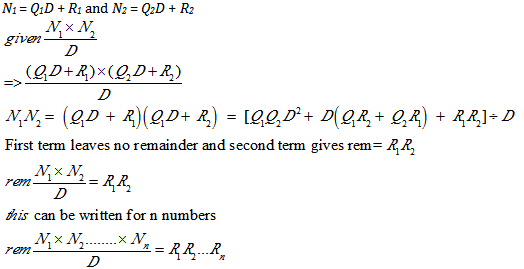
Example: What is the remainder when is divided by 12.
Solution:
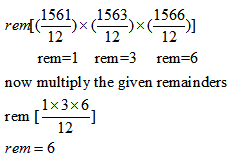
EXERCISE:
Question 1. What is the remainder when is divided by 20?
(1) 10
(2) 20
(3) 30
(4) 40
Answer and Explanation
Solution: Option 1
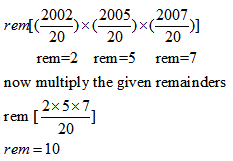
Question 2. What is the remainder when is divided by 20?
(1) 11
(2) 12
(3) 13
(4) 14
Answer and Explanation
Solution: option 4
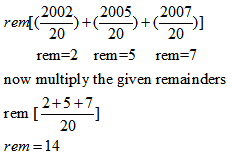
Question 3. Find the remainder when 39 is divided by 6.
(1) 1
(2) 2
(3) 3
(4) 4
Answer and Explanation
Solution: option 3
By using
Dividend = divisor * quotient + remainder
N = D*Q+R
39= 6*6+3
R=3
Question 4. What is the remainder when is divided by 2?
(1) 0
(2) 20
(3) 30
(4) 40
Answer and Explanation
Solution: option 1

Question 5. What is the remainder when is divided by 2?
(1) 10
(2) 0
(3) 30
(4) 40
Answer and Explanation
Solution: option 2








