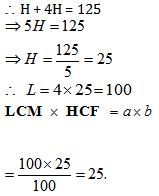LCM & HCF – Formula Application

In the previous articles on LCM and HCF, we studied the basic concepts and formulas required to solve questions. Now, we study some important shortcuts, tricks and formulas that are important from exam’s point of view.

1. LCM – LCM of two or more fractions is given by

Example: Find the LCM and HCF of 3/14, 4/15 and 5/12

Solution:

2. For two numbers a and b their product is equal to the product of their LCM and HCF hence

Example:

The LCM of two numbers is 520 and their HCF is 4. If one of the numbers is 52, then the other number is

(1) 40

(2) 42

(3) 50

(4) 52

Solution: (1)

HCF × LCM = First number × second number

52 * second number = 520 *4

Second number = 40

3. HCF of a given set of numbers is always a factor of LCM. As we know HCF is calculated by considering the least power of the numbers, which will automatically be a part of their LCM.

Example:

LCM of 12 and 18:

12= 2*2*3

18=2*3*3

LCM will be highest power ; LCM = 2*2*3*3 =36

HCF of 12 and 18 :

12= 2*2*3

18=2*3*3

HCF = 2 *3 = 6

Which is a factor of 36.

4. If ‘h’ is the HCF of two numbers ‘a’ and ‘b’ then ‘h’ is also HCF of ‘a’ and ‘a + b’. If ‘h’ is the HCF of two numbers ‘a’ and ‘b’ then ‘h’ is also HCF of ‘a’ and ‘a – b’. If ‘h’ is the HCF of two numbers ‘a’ and ‘b’ then ‘h’ is also HCF of ‘a’ and ‘a – b’ and ‘a + b’.

Example:

HCF of  12 and 18 is  6 . so HCF of  12 and 12+18=30 will also be 6 .

12= 2*2*3

30=2*3*5

HCF – 3* 2= 6

5. If for two numbers HCF = LCM then two numbers must be equal to each other.

6. For a Number n = a^pb^qc^r (here a, b & c are prime factors and p, q and r are integers then number of pairs of two number such that their LCM is N is given by: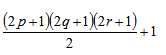

7. For three numbers a, b and c if LCM and HCF of (a, b), (b, c) and (c, a) is L_ab, L_bc, L_bc, L_ca, H_ab, H_bc and H_ca respectively then

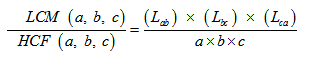
Example: prove the above property for 12,18 and 20

Solution:

12 = 2*2*3

18= 2 *3*3

20=2*2*5

LCM= 2*2*3*3*5=180

HCF = 2

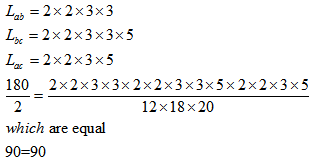
8. For two numbers A and B if HCF is h then we can assume A = hx and B = hy here x and y are co-prime to each other, and also their LCM is given by “hxy”.

Example: How many pairs of number exist such that their H.C.F is 4 & L.C.M is 48?

Solution:

Since H.C.F of two number is 4. Hence we can assume two numbers as 4x & 4y. (Here x and y are

co-prime to each other)

We know for two numbers:

H.C.F × L.C.M = Product of two numbers

Hence 4 × 48 = 4x × 4y

Or xy = 12 = 3 × 4

x = 3 and y=4 OR x=4  ,y= 3

so two pairs will exist

Example: How many pairs of two digit numbers exist such that their H.C.F is 8 & L.C.M is 120?

Solution:

Let numbers are 8x  &  8y  then 8x × 8y = 8 × 120

Or xy= 15

So pair of x  & y  is 3 & 5 that will give numbers as 24 & 40.

If we take a & b as 1 & 15 then we will get the numbers as 8 & 120 but here one of them 8 is not a two digit number. Here only one such pair exists.

9. HCF of two consecutive natural numbers is always 1.

HCF of two consecutive even natural number is always 2

Let’s apply these concepts to some more questions.

EXERCISE:

Question 1. The H.C.F. of two numbers is 96 and their L.C.M. is 1296. If one of the numbers is 864, the other is

(1) 132

(2) 135

(3) 140

(4) 144

Question 2. The smallest square number di­visible by 10, 16 and 24 is

(1) 900

(2) 1600

(3) 2500

(4) 3600

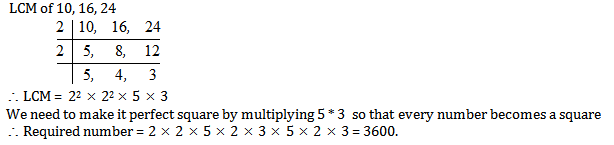
Question 3. The sum of two numbers is 84 and their HCF is 12. Total num­ber of such pairs of numbers is

(1) 2

(2) 3

(3) 4

(4) 5

Question 4.  HCF and LCM of two numbers are 7 and 140 respectively. If the numbers are between 20 and 45, the sum of the numbers, is :

(1) 70

(2) 77

(3) 63

(4) 56

Question 5.  The LCM of .two numbers is 4 times their HCF. The sum of LCM and HCF is 125. If one of the numbers is 100, then the other number is

(1) 5

(2) 25

(3) 100

(4) 125