There may be infinite number of multiples of a number. So what is an LCM?
As the name suggests, LCM is the least common multiple of two or more numbers. In other words, LCM is the smallest positive common multiple of given numbers.
Example:
LCM of 3 and 4 :
Multiple of 3 –> 3, 6, 9, 12, 15, 18,…………..
Multiple of 4 –> 4, 8, 12, 16, 20, 24,………….
So the LCM of 3 and 4 is 12, which is the lowest common multiple of 3 and 4. But this process will be very tedious if we need to calculate LCM for big numbers.
METHODS TO FIND LCM:
There are two methods to find LCM,
- Prime factorization method
- Prime divisors method
- Prime factorization method:
Step 1: write prime factors of given numbers.
Step 2: LCM will be the product of highest powers of prime factors.
Let us understand this by an example:-
Example: Find the LCM of 144, 240 and 420
Solution: To find LCM follow the steps as –
Step 1: 144 = 24 × 32
240 = 24 × 31 × 51
420 = 22 × 31 × 51 × 71
Step 2: Since highest powers of 2, 3, 5 and 7 are 4, 2, 1 and 1 respectively
So the LCM = 24 × 32 × 51 × 71 = 5040.
Example: Find the LCM of 21,36 and 66
Solution:

- Prime divisors method: –
Division method is another method to find the L.C.M. of numbers.
- First we will write the numbers in ascending order.
- Now we will divide the numbers with a common prime factor and continue the same till the time it is possible.
- We multiply all common prime factors and numbers obtained in last row to get the LCM.
Remember if a number is not divisible by this prime number, then write the number as it is
Let’s take an example to understand it:
Example: Find the L.C.M. of 24, 18 and 36
Solution:
Step 1: We arrange given numbers in ascending order i.e. we write as 18, 24 and 36.
Step 2: Here the common prime factors are 2 and 3. So we divide as shown in table below
till the time it is possible.
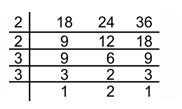
Step 3: We multiply all common prime factors and numbers obtained in last row to get LCM= 2 × 2 × 3 × 3 × 2 = 72.
Example: Find the L.C.M. of 3, 5, 8, 12?
Solution:
LCM of 3, 5, 8 and 12

Let’s try some questions based on the above-discussed concepts.
EXERCISE:
Question 1. Find LCM of 12, 18, 21, 30 by prime divisor method.
(1) 840
(2) 1260
(3) 1680
(4) 630
Answer and Explanation
Solution: Option 2
The LCM of 12, 18, 21, 30

Q2. Find LCM of 4,5,6,7,8 by prime divisor method .
(1) 840
(2) 1260
(3) 1680
(4) 630
Answer and Explanation
Solution: Option 1
LCM of 4, 5, 6, 7 and 8
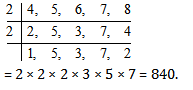
Question 3. Find LCM of 12, 18, 27, 30 by prime factorization method .
(1) 560
(2) 540
(3) 840
(4) 680
Answer and Explanation
Solution: Option 2
Step 1:

Step 2 :
Take highest power of every prime factor
LCM = ![]()
Question 4. Find LCM of 18,19,25,27 by prime factorization method.
(1) 51600
(2) 51200
(3) 51300
(4) 81400
Answer and Explanation
Solution: Option 3
Step 1:
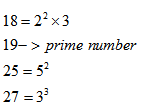
Step 2:
Take highest power of every prime factor
Lcm = ![]()
Question 5. Find LCM of 3,5,7,17 by prime factorization method.
(1) 1770
(2) 1780
(3) 1685
(4) 1785
Answer and Explanation
Solution: Option 4
3,5,7,17 all are prime numbers so we will simply multiply them
![]()







