In this article, we will understand the math behind money involved in a partnership.
So, what is a partnership? When the word Partnership is used, the first thing that comes to our mind is business between two people. In a partnership, two (or more) people invest their money to start a certain business together.
The starting money that they invest in the business is called the initial investment (normally referred to as investment). In a partnership, the entire profit and loss is divided between all the partners in the ratio of their investments.
These are some tooltips that can be used to solve questions on Partnerships:
Tooltip 1: In a partnership if money is invested for the same time-period, then that partnership is known as a simple partnership.
In a simple partnership, the profit or loss is divided between the numbers of investors in the ratio of their investments.
In other words,
If money is invested for equal amount of time, then total loss or gain will be distributed in ratio of their individual investment.
This is called simple partnership.
Ratio of investment = ratio of profit
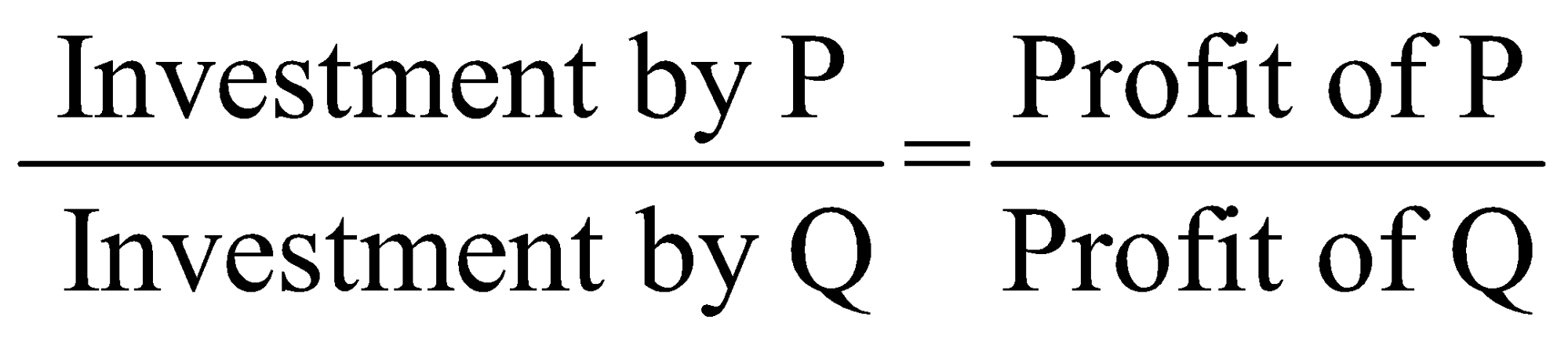
Example 1: Nitin and Mohit invested Rs 2000 and Rs 3000 respectively in some business. At the end of the year, they made a loss of Rs 1500. What is Mohit’s share of loss?
Solution:Investment by Mohit and Nitin isRs 3000 and Rs 2000 respectively
Ratio of their investment = 3:2
So, we have discussed that if the time-period is same then the loss or profit is shared between the partners in the ratio of their investment.
So, Rs. 1500 will be divided in the ratio of 3:2
So, the share of Nitin will be 2/5×1500 = Rs. 600
And the share of Mohit will be 3/5 x 1500 = Rs. 900
Let us take another example.
Example 2: Meera, Richa, Upasana invested some money in their business in ratio of 3:4:7. If their annual profit was Rs 4200 then what will be the Richa’s share?
Solution:Money invested by Meera, Richa and Upasana is in the ratio of 3 : 4 : 7
The annual profit was = Rs. 4200
So the money will be shared in the ratio of investment
So Richa’s share will be 4/14 x 4200 = Rs. 1200
Tooltip 2: If the money is invested for different time-periods, then that partnership is called a compound partnership.
In a compound investment, the profit or loss is divided between the investors in the ratio of product of their investments and time-period they invested their money for.
In other words, If money is invested for different amount of time then total loss or gain will be distributed in ratio of their individual investment × time for which the money has been invested i.e.
![]()
Example 1:Atish started the business by investing Rs. 100000. After one year, Ankraj joined with him by investing Rs. 200000. At the end of 3 years from the date they began, they earned the profit of Rs. 84000.How much more money is received by Ankraj than Atish?
Solution:
Investment of Atish = 100000 for 3 years
Investment of Ankraj = 200000 for 2 years
Total profit is = Rs. 84000
Since they invested different amount for the different interval of time
So, the ratio of investment of Atish and Ankraj=
![]()
The Total profit is Rs. 84000
So, the share of profit is also divided into 3:4.
So, the share of Atish is 3/7 x 84000 = Rs. 36000
And the share of Ankraj is 4/7 x 84000 = Rs. 48000
So Ankraj got Rs. 12000 more than the Atish
Now is the time to check whether you are through with the concepts or not. Solve the given exercise to practice questions on the above-discussed concepts.
Exercise:
Question 1: A, B and C are partners of a company. During a particular year A received one-third of the profit,B received one-fourth of the profit and C received the remaining Rs. 5,000. How much did A receive?
(1) Rs. 5,000
(2) Rs. 4,000
(3) Rs. 3,000
(4) Rs. 1,000
Answer and Explanation
Solution: (2)
We know that the Ratio of investment = ratio of profit
Let the total profit be x.
The ratio of profits of A, B and C =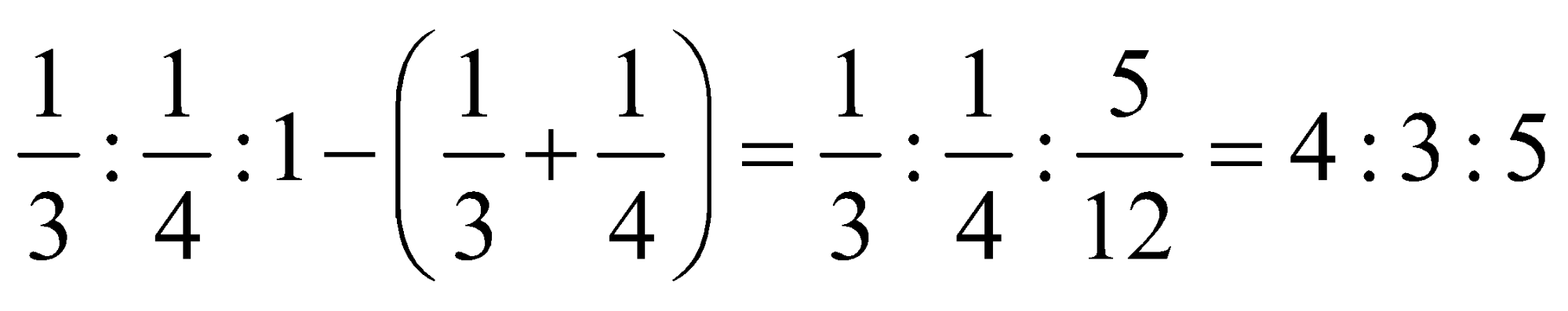
Let the profits of A, B and C be 4x, 3x, and 5x, respectively.
Given that C got Rs 5000 as profit.
Þ 5x = 5000 Þ x = Rs 1000.
Hence the amount got by A = 4x = 4 × 1000 = Rs 4000.
Question 2: A, B and C entered a partnership. A invested Rs. 2,560 and B Rs. 2,000. At the end of the year, they gained Rs. 1,105, out of which A got Rs. 320. C’s capital was
(1) Rs. 4,280
(2) Rs. 2,840
(3) Rs. 4,820
(4) Rs. 4,028
Answer and Explanation
Solution: (1)
Let the investment of C is Rs x. So, the ratio of investment of A, B and C is 2560: 2000: x.
The total profit = Rs 1105. As A received Rs 320 as profit, so we have,
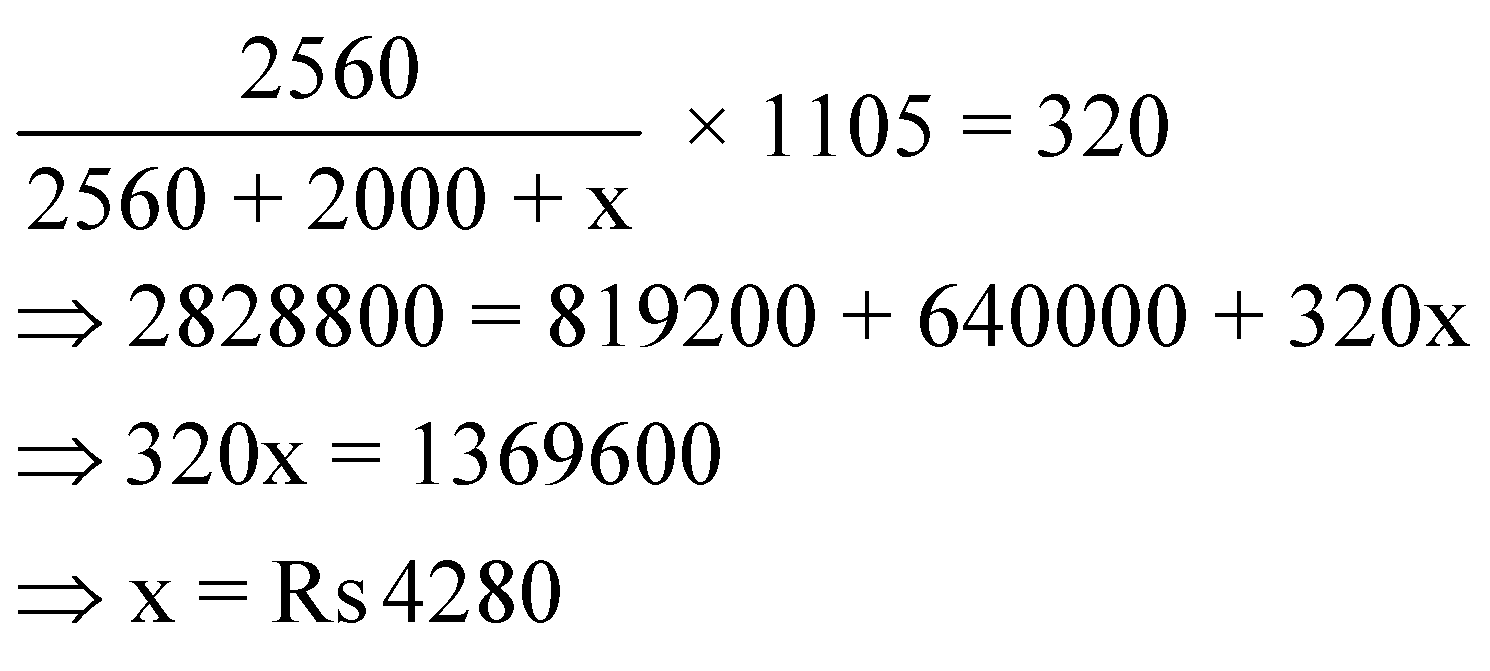
Question 3: A, B and C entered partnership in a business. A got of the profit and B and C distributed the remaining profit equally. If C got Rs. 400 less than A, what was the total profit?
(1) Rs. 1600
(2) Rs. 1200
(3) Rs. 1000
(4) Rs. 800
Answer and Explanation
Solution: (3)
Let the total profit be Rs. x.
∴ A’s share in profit = Rs.![]()
Remaining profit = Rs![]() which is divided between B and C equally
which is divided between B and C equally
So,B’s share in profit = Rs.
And C’s share in profit = Rs.![]()
According to the question,
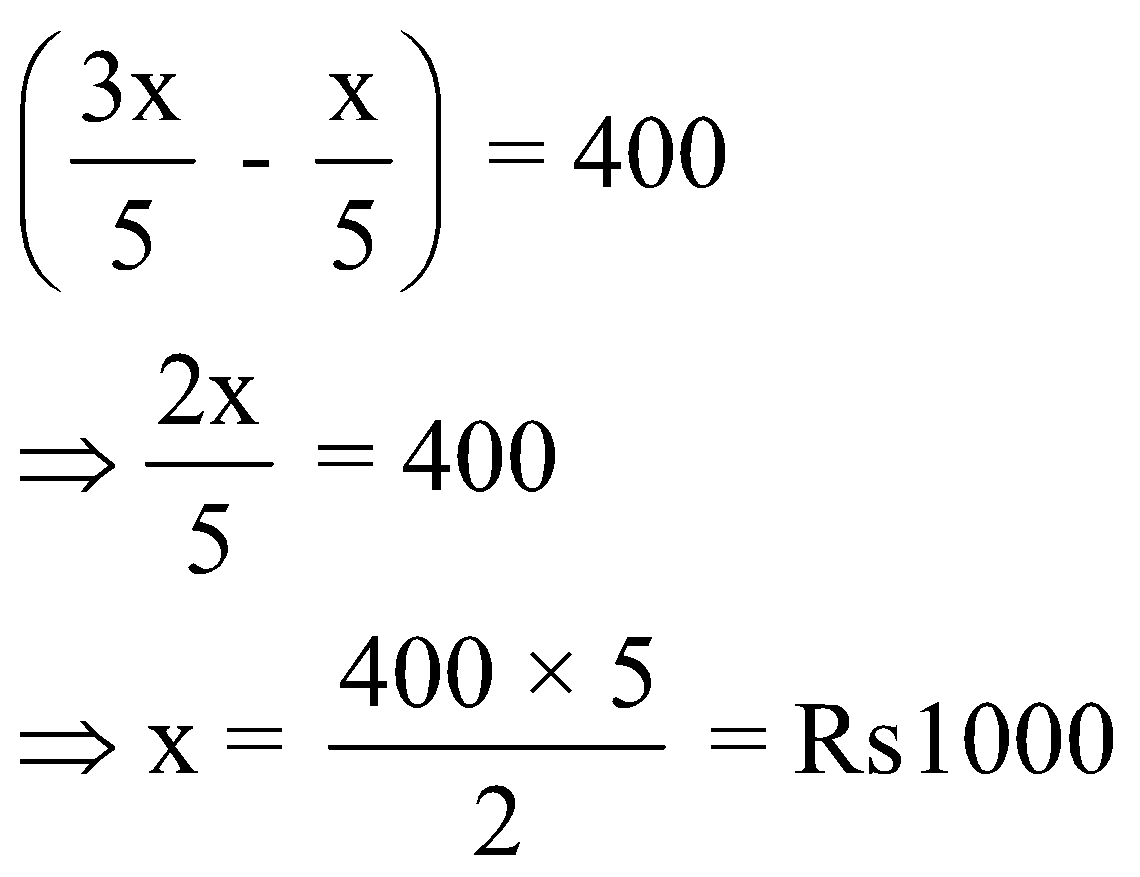
Question 4: Rs. 864 is divided among A, B and C such that 8 times A’s share is equal to 12 times B’s share and equal to 6 times C’s share. How much did B get?
(1) Rs. 399
(2) Rs. 192
(3) Rs. 288
(4) Rs. 72
Answer and Explanation
Solution: (2)
Given that 8A = 12B = 6C
⇒![]()
⇒![]()
Therefore, A : B : C = 3 : 2 : 4
∴ B’s share ![]() = × 864 =
= × 864 = ![]() Rs. 192
Rs. 192
Question 5: A, B and C entered a business, and their investments ratio was 5:4:3. After 4 months B invested Rs. 1,000 more and after 8 months C invested Rs. 2,000 more. At the end of one year the profit ratio was 15 : 14 : 11, then the investment of C at the beginning was
(1) Rs. 3000
(2) Rs. 6000
(3) Rs. 4500
(4) Rs. 7500
Answer and Explanation
Solution: (1)
Let the Initial investment of A, B and C is Rs 5x, Rs 4x and Rs 3x respectively.
∴Ratio of their equivalent capitals for 1 year
= 5x × 12 : (4x × 4 + (4x + 1000) × 8) : (3x × 8 + (3x + 2000) × 4)
= 15x : (12x + 2000) : (9x + 2000)
Now as the final profit ratio is 15: 14: 11, we have,
![]()
⇒ 14x = 12x + 2000
⇒ 2x = 2000
⇒ x = Rs. 1000
Therefore, C’s investment = 3x = Rs. 3000
Partnership Questions : Problems on Partnerships you should solve for competitive examination preparation
Welcome to this exercise on Problems on Partnerships businesses. In this exercise, we build on the basic concepts for Partnerships in business. As you prepare for your competitive examinations, you will come across questions on Partnerships in business. Such questions need optimized tackling and can be solved with ease by using simple tricks and understanding the relationships highlighted in this Partnerships Questions article. The Partnerships Questions exercise comes into the picture where it gives you a chance to practice the highlighted and important concepts related to Partnerships question type.













