n the previous article, we studied about different types of numbers. Now, in this article we will discuss prime and composite numbers in detail.
Prime numbers
Numbers, which don’t have any factor other than 1 or itself, are said to be prime numbers.
For example 2, 3, 5, 7, 11, 13, 17,………………
Or we can say that the numbers which are not divisible by any other number except 1 and itself are called prime numbers.
Properties of Prime Numbers
- If p is any prime number and p divides a product of two integers say m and n i.e. p|mn
(read as p divides mn), then p divides ‘m’ or p divides ‘n’ or both.
e.g. 14X17 is divisible by 7 as 14 is divisible by 7.
- Number of prime numbers is uncountable. i.e. there are infinite prime numbers.
- Every Prime number has exactly two factors or divisors. For example: 13 is prime number as the divisors of 13 are 1 and 13.
- There is only one even prime i.e. 2 and all other primes are odd. 2 is also the smallest prime number.
- G.C.D of prime numbers is always 1. The numbers whose G.C.D is 1 are said to be co-prime. Thus, we can say that two primes are always co-prime.
We can understand it this way, If Greatest common divisor of two numbers is 1, in layman’s terms, it means that there is no common factor in those two numbers, then those numbers will be co prime.
For e.g.: – Consider two prime numbers 7 and 17. Greatest number that can divide them both simultaneously is 1. It means their GCD is 1. Therefore, they are co-prime.
- The Twin Primes are pair of primes of the form (p, p+2). It is conjectured that there are an infinite number of twin primes.
For e.g. 3,5 are twin prime and so are 5,7. There can be infinite such pairs.
- The term odd prime refers to any prime number greater than 2. For example: 3, 5,7, …………..
- 1 is neither prime nor composite number.
- All prime numbers greater than 3 can be expressed in the form of 6n-1 or 6n+1 i.e. all prime numbers, which are greater than 3 leave remainder 1 or 5 when divided by 6.
For e.g. When 13 is divided by 6 it gives remainder 1.
When 19 is divided by 6 it gives remainder 5.
- For prime numbers p greater than 3,
 is divisible by 24
is divisible by 24 - Prime numbers of the form
 , where n is also a prime number, are Mersenne’s prime numbers. For e.g. 3, 7, 31, etc.
, where n is also a prime number, are Mersenne’s prime numbers. For e.g. 3, 7, 31, etc.
(It is not the case with every prime value of n. for e.g. ![]() is not prime.)
is not prime.)
List of prime numbers with number ranges:

Tip: You should learn prime numbers from 1 to 100 to solve questions quickly.
The yellow colored numbers are prime numbers from 1 to 100.

How can you check whether the given number is prime or not?
The below tip can be used to check whether a given number N is prime or not:
First of all, find the square root of that number N and then approximate that to immediately lower integer (say n) and write down all the prime numbers less than that integer (n). Then check the divisibility of the given number N by all the prime numbers we have written in previous step. If it is not divisible by any of the prime numbers, then the given number N is prime.
Let us write algorithm for the same.
Step 1: Find square root of N, call it as K (Just find approximate values, rounded off to the lower integer)
Step 2: Write down all the prime numbers less than K.
Step 3: Check divisibility of N with these prime numbers, which we have got in Step 2.
Step 4: If N is not divisible by any of the prime numbers then N is prime.
Example 1:
Let us check whether 211 is prime or not?
Solution:
Step 1: We find square root of 211 i.e. K= = 14.52. Approximating it to immediately lower integer, we get K=14.
Step 2: We write all primes less than 14, i.e. 2, 3, 5, 7, 11 and 13.
Step 3: Now, we check the divisibility of 211 by all the prime numbers of step 2.
Step 4: Since 211 is not divisible by any of these prime numbers, hence 211 is a prime number.
Example 2:
Let us check whether 313 is prime or not?
Solution:
Step 1: We find square root of 313 i.e. K= ![]() = 17.69
= 17.69
Step 2: We write all primes less than 17.69 i.e. 2, 3, 5, 7, 11, 13 and 17
Step 3: Now, we check the divisibility of 313 by all the prime numbers of step 2.
Step 4: Since 313 is not divisible by any of these prime numbers, hence 313 is a prime number.
Composite numbers
Composite numbers are those numbers which can be written as the product of prime numbers in a unique way.
e.g. 15 = 3 × 5, 100 = 2 × 2 × 5 × 5
Or we say that if a number has more than two factors then it is said to be a composite number.
Try out the given exercise to get a better hold of the above-discussed concepts.
EXERCISE:-
Question 1:
1. Is 91 a prime number?
2. Yes
3. No
Answer and Explanation
Solution: As 91 = 13 × 7. Hence 91 can be written as the product of two prime numbers. So, it is not a prime number. Hence, answer is option (b)
Question 2: It is given that (![]() ) is completely divisible by a whole number. Which of the following numbers is completely divisible by this number?
) is completely divisible by a whole number. Which of the following numbers is completely divisible by this number?
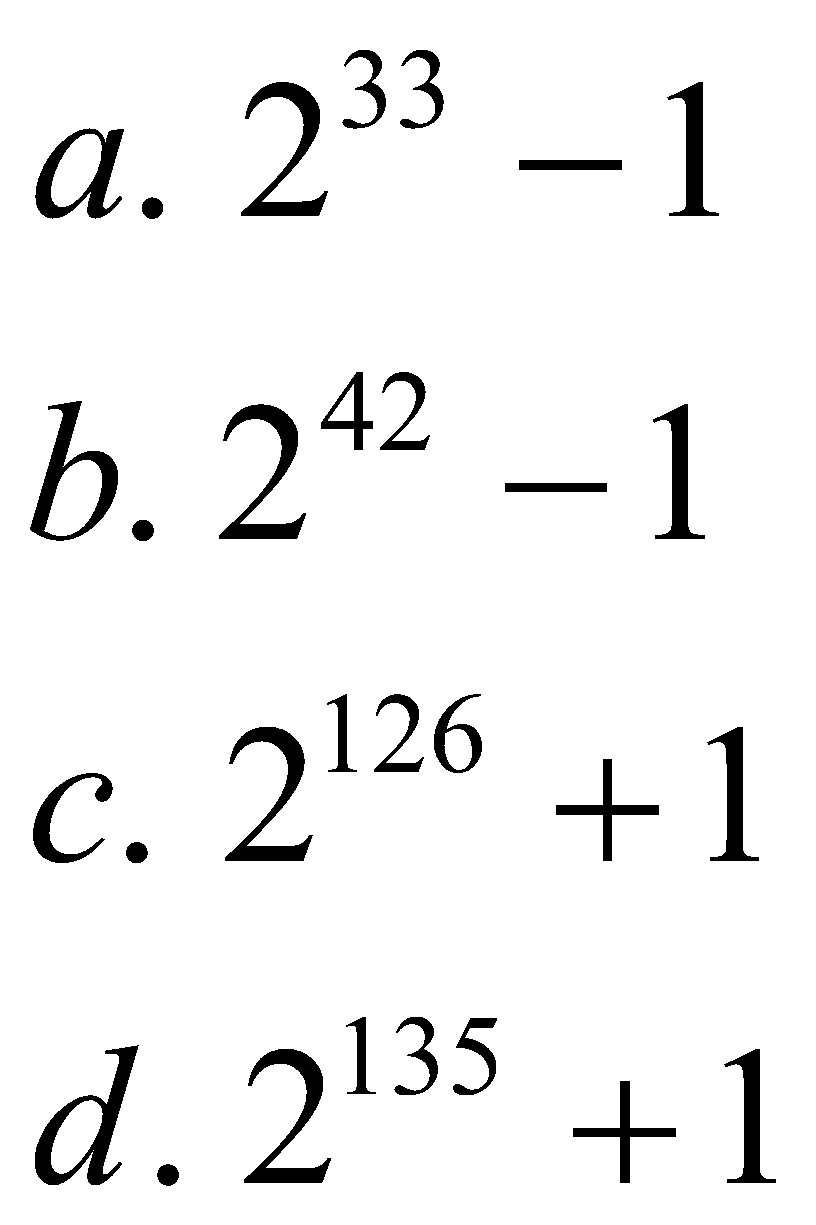
Answer and Explanation
Solution: We will check the options.
In option c we have 2126 +1 = (242) 3 + 1 = (242 + 1){(242) 2 – 242 + 1}
(We have basically expanded (a3+b3)=(a+b)(a2+b2-ab) ).
Now as (242 + 1) is divisible by a certain number say ‘x’ then 2126 +1 is also divisible by the same number ‘x’. Hence, (c)
Question 3: Which number is smallest prime number?
a. 2
b. 3
c. 5
d. 1
Answer and Explanation
Solution: 2 is the smallest prime number. Hence, option (a)
Question 4: What is the sum of first 5 odd prime numbers?
a. 27
b. 29
c. 39
d. 40
Answer and Explanation
Solution: First 5 odd prime numbers are: – 3, 5, 7, 11, 13
Their sum = 3+5+7+11+13=39
Hence, option (c)
Note: 1 is not a prime number.
Question 5: What is the sum of first 5 composite numbers?
a. 30
b. 37
c. 29
d. 28
Answer and Explanation
Solution: First 5 composite numbers: – 4,6,8,9,10
Their sum = 4+6+8+9+10=37.
Hence, option (b).







