CAT 2022 Profit and Loss: Concept of Discounts and Marked Price Explained
In the first part of Profit and Loss series, we learnt the basic definitions and the meaning of Cost Price, Selling Price, Marked price etc. Let us revise the definition of Marked Price. As we saw earlier, traders are in the habit of marking their articles at a certain price above their costs. Then the discounts they offer are on this marked price, thereby they actually make sure that have already factored in the profit they want.

Discounts are offered on the marked price and the selling price is determined by the discount offered on the marked price. For the process of simplification, let us assume:
C = Cost price
S = Selling price
M = Market price
D% = Discount
G% = Gain
Now,
Discount = D% of marked price, M
Discount = Marked Price – Selling Price
Marked Price – Amount of Discount = Selling Price
M (1-D%) = Selling Price
Also, Selling Price = Cost Price + Gain
Thus,
M (1-D%) = C (1 + G%)
Or in other words
Marked Price (1 – Discount%) = Cost Price (1 + Gain%)
Example-1: Natasha offers her customers a discount of 10% on her beauty products and she still makes a profit of 20%. What is the actual cost to her of that beauty product marked Rs. 400?
Solution:
Marked price = Rs. 400
Discount = 10%
Profit = 20%
Therefore, the Selling Price = 90% of 400
Therefore 400 x 90/100 = Rs. 360
Selling price = Rs. 360
Profit = 20%
Cost price = 100/120 x 360 = Rs. 300
CAT 2022 Profit and Loss: Concept of successive discounts
If successive discounts of x% and y% are allowed on the marked price M of the discount, then, after discount the customer finally ends up paying:
Selling Price = (1-x%)(1-y%) x Marked Price
If you look at the above formula closely, you would see that the multiplication is nothing else but a percentage equivalent of two successive percentage change on a number.
Example-2: Pankaj offers a 10% discounts on his goods and he offers a further discount of 5% on the reduced price to those customers who pay cash. What does a customer have to pay in cash for a cricket bat of Rs. 200?
Solution:
Price of the cricket bat = Rs. 200
After Discount of 10% Marked price would be Rs. 180
Since he is purchasing the bat by cash, so a discount of 5% is applicable again on the reduced marked price. Thus, the final selling price the cricket bat would be of Rs. 171
CAT 2022 Profit and Loss: Basic Question types
Type-1: Comparing quantities of goods and prices
In these types of questions, CP of a fixed number of goods are compared with the SP of another field number of goods. Let us see through an example:
Example-3: The cost price of 30 articles is equal to the selling price of 40 articles. What is the profit or loss percentage?
Solution:
To obtain the same amount of money, which was needed to purchase 30 articles, we need to sell 40 articles, which is more than what we have got for the same sum. It means we need to arrange 10 more articles apart from the articles which we have purchased. So, there will be a loss.
Now, CP of 30 articles = SP of 40 articles Or, CP/SP = 30/40 =3/4
Or, 1 – CP/SP = 1- 3/4 = 1/4
So, Loss percentage
= (l – CP/SP) x 100 = 1/4x 100 = 25%
Alternatively,
CP of 30 articles = SP of 40 articles = Rs 120 (Assume) So, CP of one article = Rs 4 ,SP of one article = Rs 3 Obviously, there is a loss of Re 1 Loss percentage = 1,4 X 100 = 25%
Type 2: Questions in terms of money
In this type of question, we generally talk about the cost price and selling price questions there are some results which helps us to solve typical these type of questions
Some Important Results
When SPs of two articles are same
1. First one is sold at a profit of x% and second one is sold at a profit of y%.
Ratio of CP1:CP2 (100 + y) : (100 + x)
2. First one is sold at a profit of x% and second one is sold at a loss of y%.
Ratio of CP1:CP2 = (100 – y): (100 + x)
3. First one is sold at a loss of x% and second one is sold at a loss of y%.
Ratio of CP1: CP2 = (100 – y): (100 – x)
4. First one is sold at a loss of x% and second one is sold at a profit of y%.
Ratio of CP1: CP2 = (100 + y): (100 – x)
Type-3: Miscellaneous Problems based on % gain and % loss
Example-4: Bharat purchased 90 bags of cement at Rs. 450 each. He sold 30 bags at 20% profit and 20 bags at 6% loss. At what rate per bag should the remainder he sold to gain a profit of 9% on whole transaction
Solution:
This question type is nothing else but a combination of ratio and proportion with profit and loss. In this case, we can solve the question in the following manner:
According to the information given, bags remaining = 40
Let the 40 bags be sold with p% gain
Now % gain or loss on the whole lot
= sum of product of gain or loss %s with their respective quantities
Therefore
9% of 90 Bags of Rs. 450 each = 20% of 30 Bags of Rs. 450 each – 6% of 20 Bags of Rs. 450 each +9% of 40 Bags of Rs. 450 each
(9/100) x 90 x 450= {(20/100) x 30 x 450} – {(6/100) x 20 x 450} + {(p/100) x 40 x 450}
9 x 90 = (20 x 30) – (6 x 20) + (p x 40)
p = 8.25%
Therefore, the selling price would be = 108.25/100 x 450 = Rs. 487.125
CAT 2022 Profit and Loss: Discounts and Marked Price Practice Exercise
Question 1:
A shopkeeper offers 20% discount and still makes profit of 25%. Calculate the cost of article which has a marked price of Rs 200.
a. Rs. 130
b. Rs. 128
c. Rs. 125
d. Rs. 140
Answer and Explanation
Apply formula
Marked price (1-discount%)= Cost price (1+profit%)
200(1-0.2)= Cost price (1+0.25)
Cost Price = (200 x 0.8)/1.25 = Rs. 128
Question 2:
A merchant fixes the sale price of his goods at 15% above the cost price. He sells his goods at 12% less than the fixed price. His percentage of profit is :
(a) 2.5%
(b) 1.2%
(c) 1.5%
(d) 2%
Answer and Explanation
Let the cost price be Rs. 100.
Marked price = Rs. (100 + 15% of 100) = Rs. 115
The goods are sold at the discount of 12%.
S.P. = (115 – 12% of 115)
= Rs. (115 – 13.80) = Rs. 101.20
Profit = Rs. (101.20 – 100) = Rs. 1.20
Question 3:
A dealer makes a profit of 20% even after giving a 10% discount on the advertised price of a scooter. If he makes a profit of Rs. 7500 on the sale of the scooter, the advertised price was
(a) Rs. 45000
(b) Rs. 47500
(c) Rs. 50000
(d) Rs. 52500
Answer and Explanation
The advertising price is basically the marked price.
The dealer makes a profit of 20% after giving a 10% discount, so
marked price (1-discount%)=cp(1+profit%)
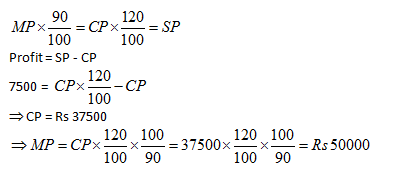
Question 4:
If a man were to sell his chair for Rs. 720, he would lose 25%. To gain 25% he should sell it for
(a) Rs. 1,200
(b) Rs. 1,000
(c) Rs. 960
(d) Rs. 900
Answer and Explanation
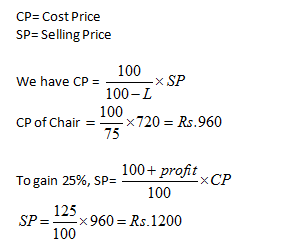
Question 5:
A man bought an old typewriter for Rs. 1200 and spent Rs. 200 on its repair. He sold it for Rs. 1680. His profit per cent is:
(a) 20%
(b) 10%
(c) 8%
(d) 16%
Answer and Explanation
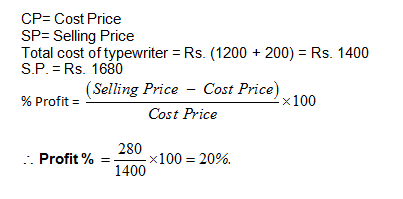








Very good sir
I like way of your explanation. Send all the difficult and different types of problems.