An important problem type you would encounter in profit and loss involve the use of false weights. Generally, in a false scale, the actual value of the weight is lower than the true one and this enables a gain for the shopkeeper by selling a lesser quantity than disclosed by him.
Dishonest Dealer: A dishonest dealer is one who claims to sell his product in welfare of customer but either he alters weight or he marks up price too high and then gives discount to attract customers.
Let us assume that the shopkeeper makes a gain of G% in selling his product.
Therefore,
(100+G)/(100+x) = True weight/ False weight
Here,
G = Overall gain percentage
X = %loss or % gain
Also, another formula that you can remember, in case the shopkeeper sells at the cost price, is:
Gain Percentage
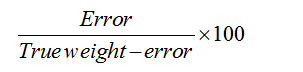
Let us check this formula by taking an example.
Let us say that I went to a shop to by 1kg almonds. The shopkeeper told me that he is selling the almonds at the cost price but he actually used a faulty weight and gave me only 800gm. Let the cost which the shopkeeper paid for 1 kg was Rs 1000 and as he told me that he is selling at the cost price so I will pay him Rs 1000 for 1kg. But what I am getting instead 1kg, only 800gm. Now try to understand the logic. The shopkeeper sold me 800 gm almonds for Rs 1000 for which he actually paid Rs 800 (cost price of 800gm). So he gained 1000 – 800 = Rs 200 and his percentage profit = (200/800)x100
which is same as given above in the formula. Here 200 is the error and 800 = 1000 – 200 = True weight – Error.
So how to proceed with the problems when the shopkeeper is selling the articles at a price different from that of cost price while using faulty weight? In this case the shopkeeper will make two profits. First profit is because of the wrong weight and the second is because of the actual difference between the cost price and the selling price. The final profit percentage is arrived by using the result {P + Q + (PQ/100)} where P and Q are the two profits.
Let us understand it by a example.
Example 1: Let a dishonest shopkeeper sells sugar at Rs 18/kg which he has bought at Rs 15/kg and he is giving 800gm instead of 1000gm. Find his actual profit percentage.
Solution: Here the cost price of the sugar = Rs 15/kg
The selling price = Rs 18/kg.
The profit made by the shopkeeper is of Rs 3 and the profit percentage = 3/15 x 100 = 20%
This will be his total profit if he has actually sold 1 kg sugar. But that is not the case here as he is using the false weight.
Now the profit due to wrong weight =
![]()
= (200/800)x100 = 25%
The overall profit percentage = {P + Q + (PQ/100)} = [20+25+{(20 x 25)/100}] = 50%
You can also attempt this problem by another method.
The cost price of 1kg sugar is Rs 15. As the shopkeeper is giving only 800gm so the cost price of the 800 gm sugar is Rs 12. Here we have calculated the cost price of 800gm sugar because the shopkeeper is actually selling only 800gm. He is selling 800 gm sugar for Rs 18 for which he had paid Rs 12. So he gained Rs 6 and the profit percentage = 6/12 x 100 = 50%
The answer in this case is same as calculated above but the first method is more easy than the second one. Just find the individual profits and put the values in {P + Q + (PQ/100)}
The above formula is also valid if the shopkeeper is making losses due to some reason. In that case you will put the negative value for the loss. Let us take an example.
Example 2: A shopkeeper claims that he is selling sugar at Rs 23/kg which cost him Rs 25/kg but he is giving 800gm instead of 1000gm. What is his percentage profit or loss?
Solution: Here the cost price of the sugar is Rs 25/kg and the selling price is Rs 23/kg. So the loss is Rs 2/kg and the loss percentage = 2/25 x 100 = 8%
The profit due to wrong weight = 200/800 x 100 = 25%
Hence the overall profit and loss is given by {P + Q + (PQ/100)}
But as he is making loss of 8% in the first case so we put -8 in the above expression. If the final value is positive then he is making profit otherwise loss. So the net profit and loss =
{25 – 8 + {25 x (-8)}/100} = 25 – 8 – 2 = 15%
As the final value is positive so he is making a profit of 15%.
Example-3: Lalit marks up his goods by 40% and gives a discount of 10%. Apart from this, he uses a faulty balance also, which reads 1000 gm for 800 gm. What is his net profit percentage?
Solution:
Let us assume his CP/1000 gm = Rs 100
So, his SP/kg (800 gm) = Rs 126
So, his CP/800 gm = Rs 80
So, profit = Rs 46
So, profit percentage = 46/80 x 100 = 57.5%
Shortcuts for Faulty Weights Questions:
Case-1: When dealer reduces weight in terms of percentage and earns profit
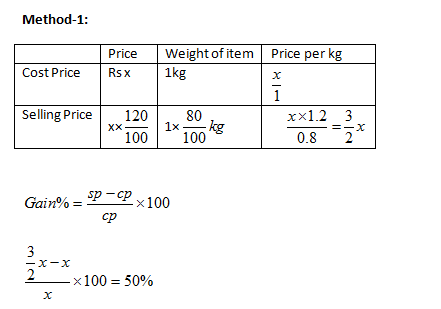
Example: A shopkeeper sells an item at a profit of 20 % and uses a weight which is 20% less. Find his total profit.
Solution:
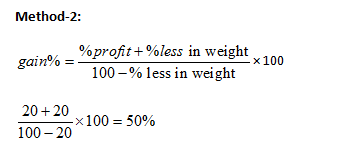
Case-2: When dealer sells goods at loss on cost price but uses less weight.
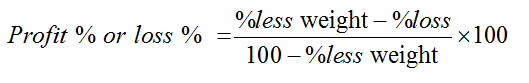
Note :- profit or loss will be decided according to sign . If +ive it is profit ,if –ve it is loss.
Example: A dishonest dealer sells goods at 10% loss on cost price but uses 20% less weight. Calculate profit or loss percent.
Solution:
Apply formula:
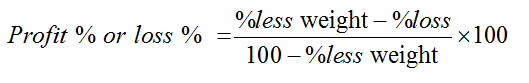
{(20-10)/(100-20)} x 100 = 25/2%
Here sign is positive so there is a profit of 12.5%
Case-3: When dealer sells product at loss but alters weight :-
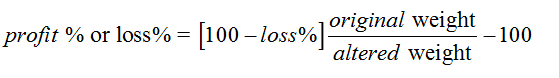
Note :- Profit or loss will be decided according to sign .if +ive it is profit ,if –ve it is loss .
Example: A dishonest dealer sells products at 10% loss on cost price but uses 2 gm instead of 4 gm . what is his profit or loss percent?
Solution:
Apply formula :
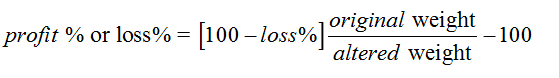
[100-10] 4/2-100=80%
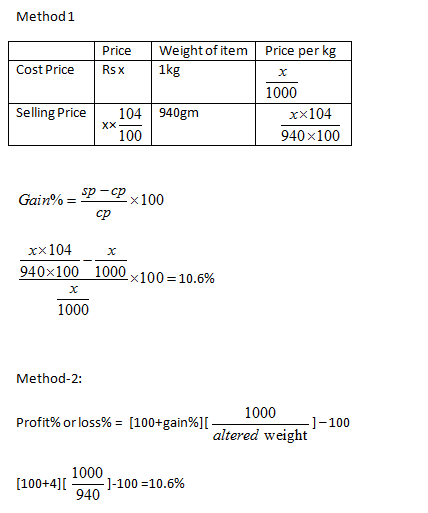
Case-4: When dealer sells product at profit but alters weight
Profit% or loss% = [100+gain%][1000/altered weight ] – 100
Note :- Profit or loss will be decided according to sign. If +ive it is profit ,if –ve it is loss .
Example: A shopkeeper uses 940 gm in place of one kg. He sells it at 4% profit. What will be the overall profit or loss?
Solution:
Profit and Loss: Dishonest Dealers and Faulty Weights Exercise:
Question 1:
A dishonest dealer professes to sell his good at cost price but uses a false weight and thus gains 20%. For a kilogram he uses a weight of
(a) 700g
(b) 750g
(c) 800g
(d) None of these
Answer and Explanation
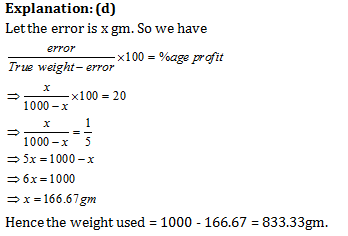
Question 2:
A grocery dealer cheats to the ex¬tent of 10% while buying as well as selling by using false weight. What is his increase in the profit % ?
(a) 20%
(b) 21%
(c) 22%
(d) None of these
Answer and Explanation
Option (b)
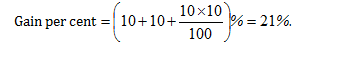
Question 3:
A shopkeeper wants to make some profit by selling rice. He contemplates about various methods. Which of the following would maximise his profit ?
I. Sell rice at 15% profit.
II. Use 850 g of weight instead of 1 kg.
III. Mix 15% impurities in rice and selling rice at cost price.
IV. Increase the price by 7.5% and reduce weights by 7.5%.
(a) I or III
(b) II
(c) II, III and IV
(d) Profits are same
Answer and Explanation

Question 4:
A dealer buys apples at Rs.50, Rs. 40 and Rs. 30 per kilogram. He mixes them in the ratio 2 :4 : 9 by weight, and sells at a profit of 30%. At what approximate price per kilogram does he sell the dry fruit ?
(a) Rs 54
(b) Rs 77
(c) Rs 67
(d) Rs 46
Answer and Explanation
Answers: (d)
Cost price of (2 + 4 + 9) = 15 kg of fruits = Rs. (100 + 160 + 270) = Rs. 530
S.P. at a profit of 30% = 530 × 1.3 = Rs 689
∴ S.P. of fruits per kg =689/15 = 45.93 approx. Rs. 46/kg
Question 5:
A dishonest shopkeeper, using a faulty balance makes a profit of 5% while buying as well as while selling his goods. His ac¬tual gain percent in the whole process amounts to
(a) 11
(b) 10
(c) 10.25
(d) 10.5
Answer and Explanation
Option (c)
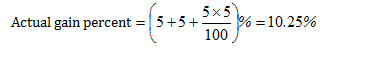










Very very helpful content
The formulas are very helpful and saves aa lot of time .
Thank you
Content is very good.
Please Make the site little bit more readable (font-size, space)
A shopkeeper wants to make some profit by selling rice. He contemplates about various methods. Which of the following would maximise his profit ?
I. Sell rice at 15% profit.
II. Use 850 g of weight instead of 1 kg.
III. Mix 15% impurities in rice and selling rice at cost price.
IV. Increase the price by 7.5% and reduce weights by 7.5%.
(a) I or III
(b) II
(c) II, III and IV
(d) Profits are same
can you please explain this with some other method?