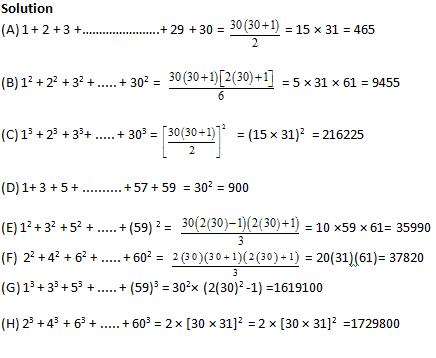Properties of Addition of Natural Numbers

Properties of Addition of Natural Numbers:
Sum of 1^{st ‘}n’ Natural numbers =  1 + 2 + 3 + …. + n = $\frac{n\left( n+1 \right)}{2}$

Sum of squares of 1^st ‘n’ natural number  =  1² + 2² + 3² + ….. + n²  = $\frac{n\left( n+1 \right)\left( 2n+1 \right)}{6}$

Sum of cubes of 1^st ‘n’ Natural number  =  1³ + 2³ + 3³ + ….. + n³  = ${{\left( \frac{n\left( n+1 \right)}{2} \right)}^{2}}$

Sum of 1^st ‘n’ Odd natural number  =  1+ 3 + 5 + ….. + (2n – 1)  = n²

Sum of 1st ‘n’ even natural numbers  = 2 + 4 + 6+ …….2n = n (n+1)

Sum of squares of 1^st ‘n’ Odd natural number = 1² + 3² + 5² + ….. + (2n – 1) ² = $\frac{n\left( 2n-1 \right)\left( 2n+1 \right)}{3}$

Sum of squares of 1^st ‘n’ Even natural number =  2² + 4² + 6² + ….. + (2n)² = $\frac{2n\left( n+1 \right)\left( 2n+1 \right)}{3}$

Sum of cubes of 1^st  ‘n’ Odd natural number =  1³ + 3³ + 5³ + ….. + (2n -1)³ = n² (2n² -1)

Sum of cubes of 1^st  ‘n’ Even natural number  =  2³ + 4³ + 6³ + ….. + (2n)³ = 2 [n (n + 1)]²

Some examples for the above properties:

Find the sum of:

(A) First 30 natural numbers

(B) Squares of first 30 natural numbers

(C) Cubes of first 30 natural numbers

(D) First 30 odd natural numbers

(E) Squares of first odd 30 natural numbers

(F) Squares of first even 30 natural numbers

(G) Cubes of first odd 30 natural numbers

(H) Cubes of first even 30 natural numbers