So far, we have discussed Ratios. In this article, let us investigate the basics of Proportion.
Definition:
When two ratios are equal,then the ratios are called proportional, that is, when,
![]()
then a,b,c, and d are said to be in proportion.
This is also represented as a: b :: c: d and read as a is to b is as c is to d .
In the relation given above:
- a and d are labeled as extremes.
- b and c are labeled as means.
Important Properties for Proportion:
- Product of extremes = product of means
What does this mean?
If
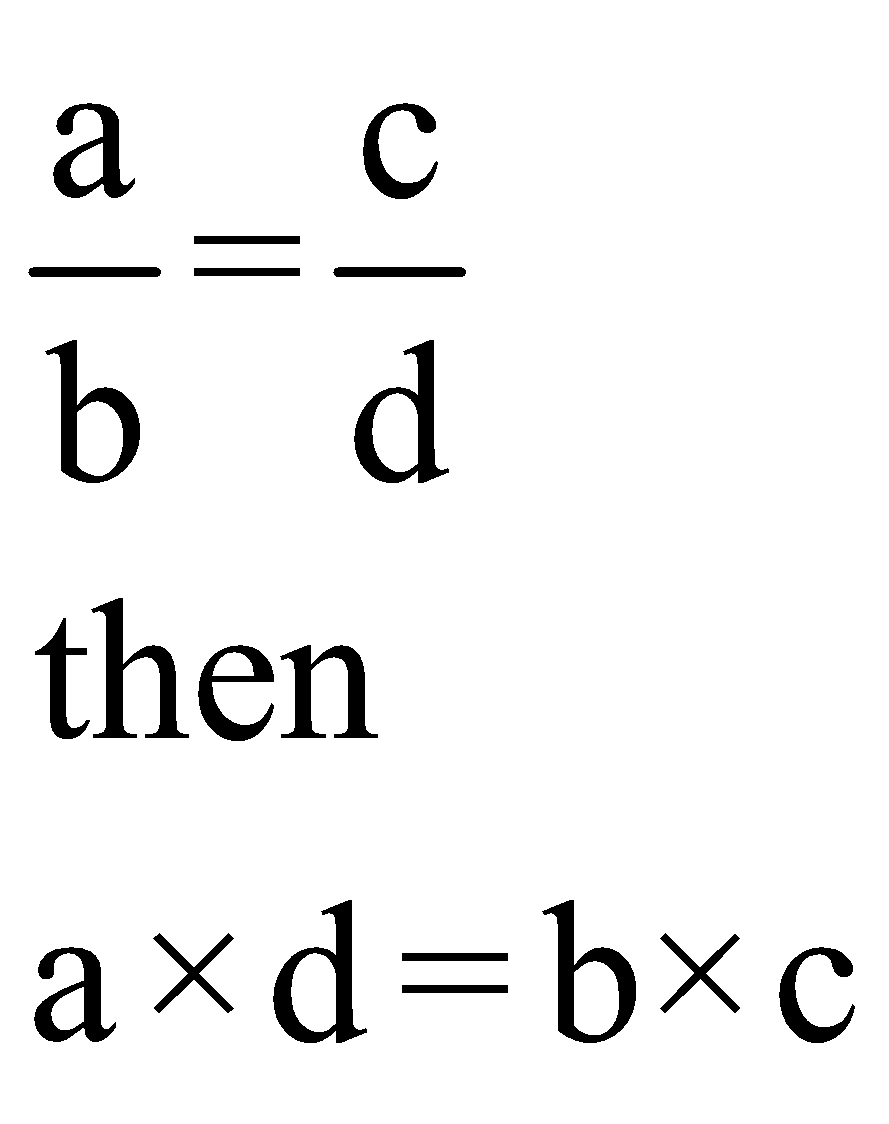
2. Inverse proportion or Invertendo
The following is called an inverse proportion or invertendo:
If
![]()
3. Componendo and Dividendo
If![]() , then
, then
(i) ![]() (Componendo)
(Componendo)
How can we prove this result?
Add 1 to each side of the given ratio and we will have this result.
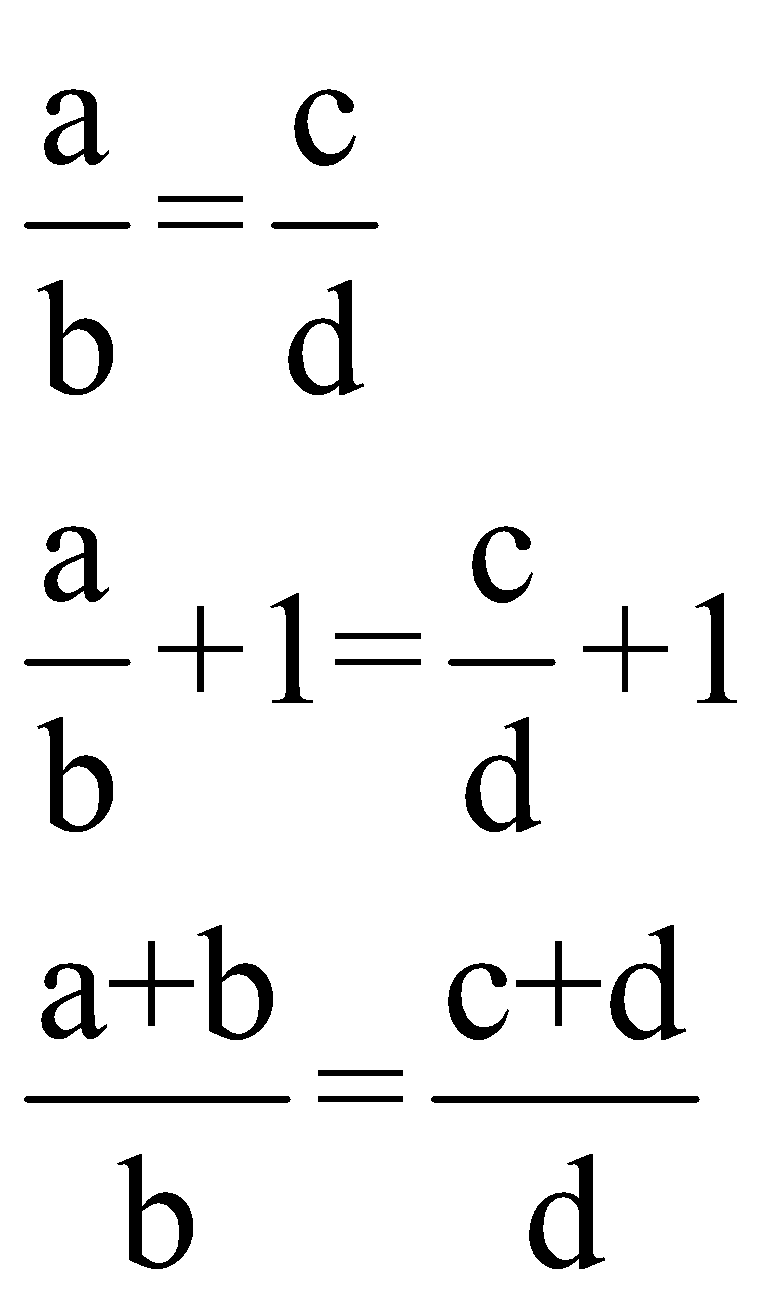
(ii)![]() (Dividendo)
(Dividendo)
How can we prove this result?
Subtract 1 from each side of the given ratio and we will have this result.
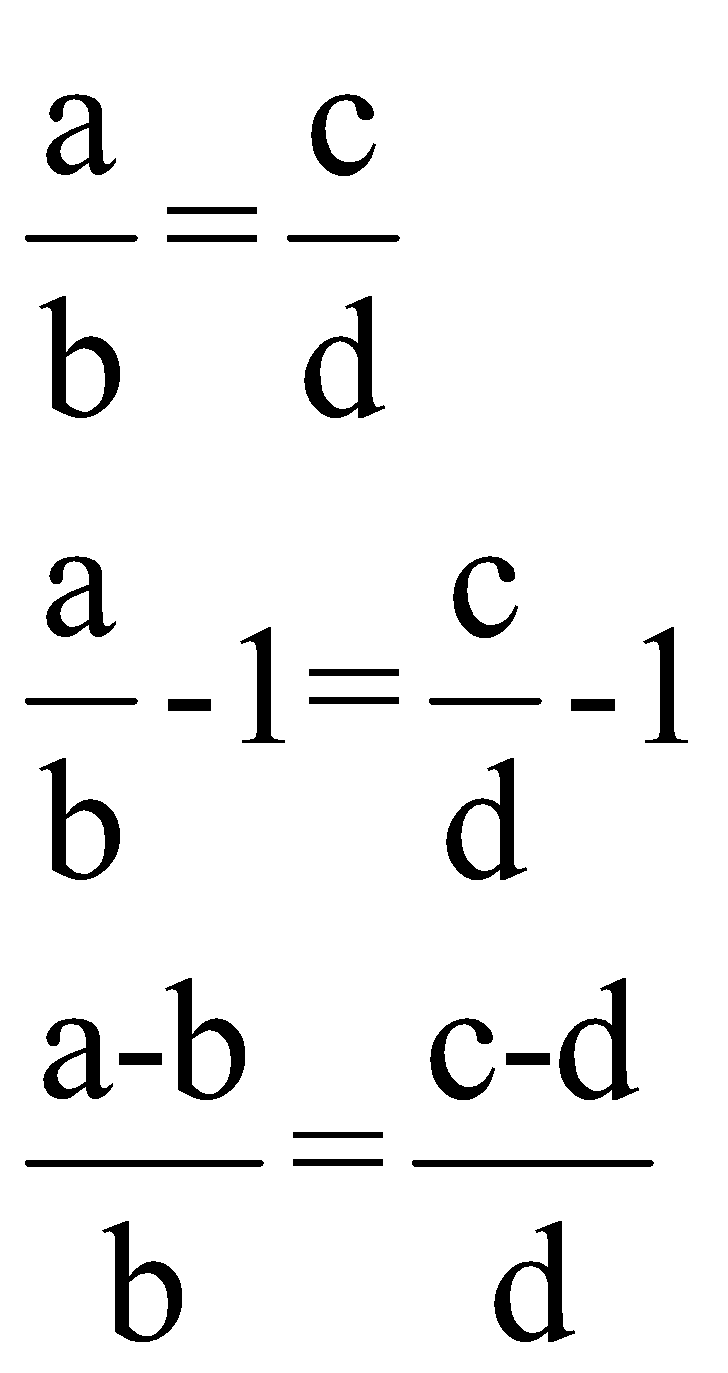
(iii) ![]() (Componendo and Dividendo)
(Componendo and Dividendo)
Proof:We have
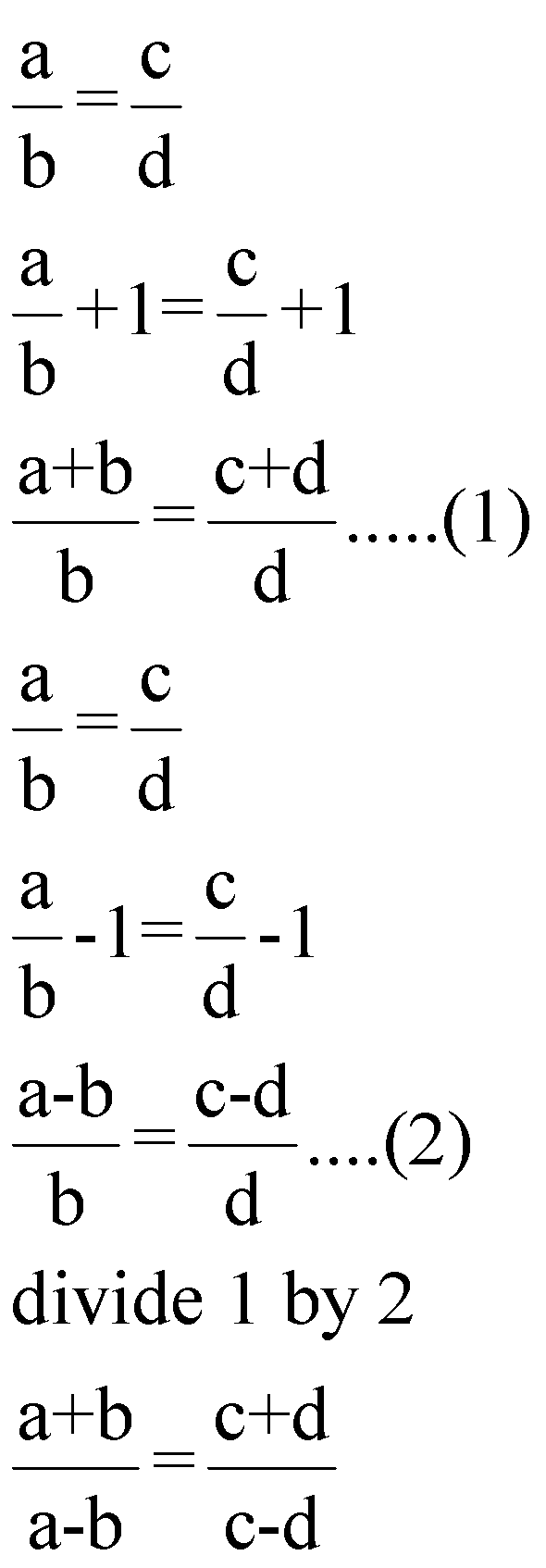
(iv)![]()
We have
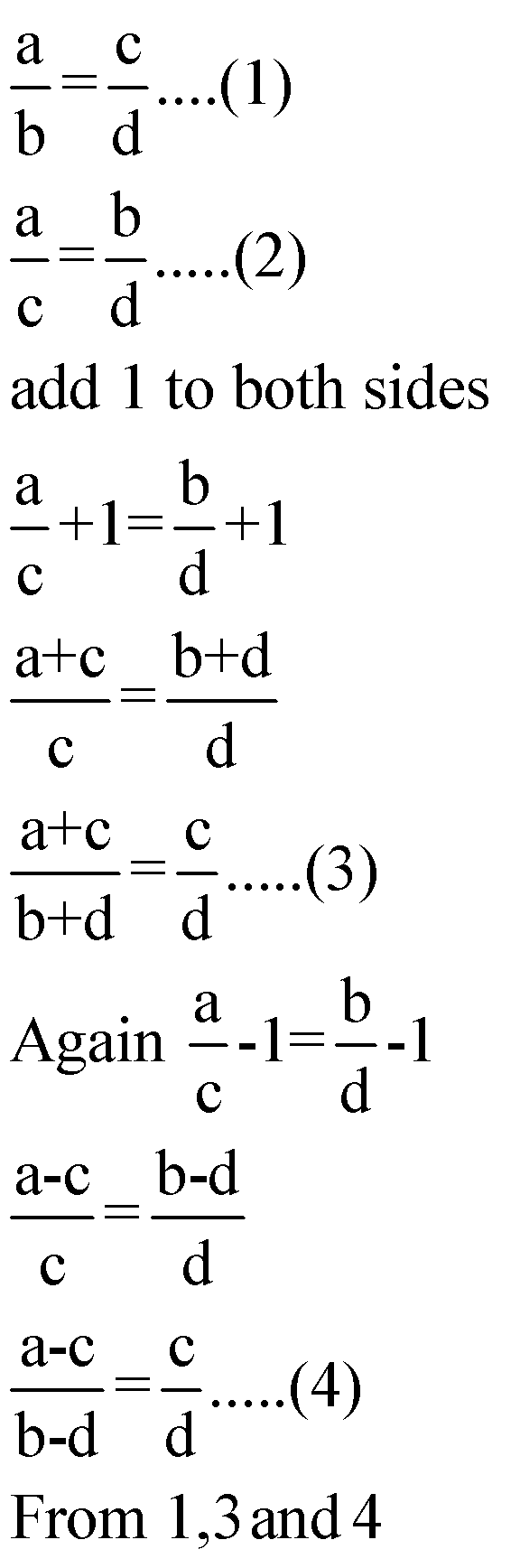
![]()
4. Continued Proportion
3 terms or quantities of the same kind are said to be in continued proportion when the ratio of the 1st to the 2nd is equal to the ratio of the 2nd to the 3rd.
Effectively, this means:
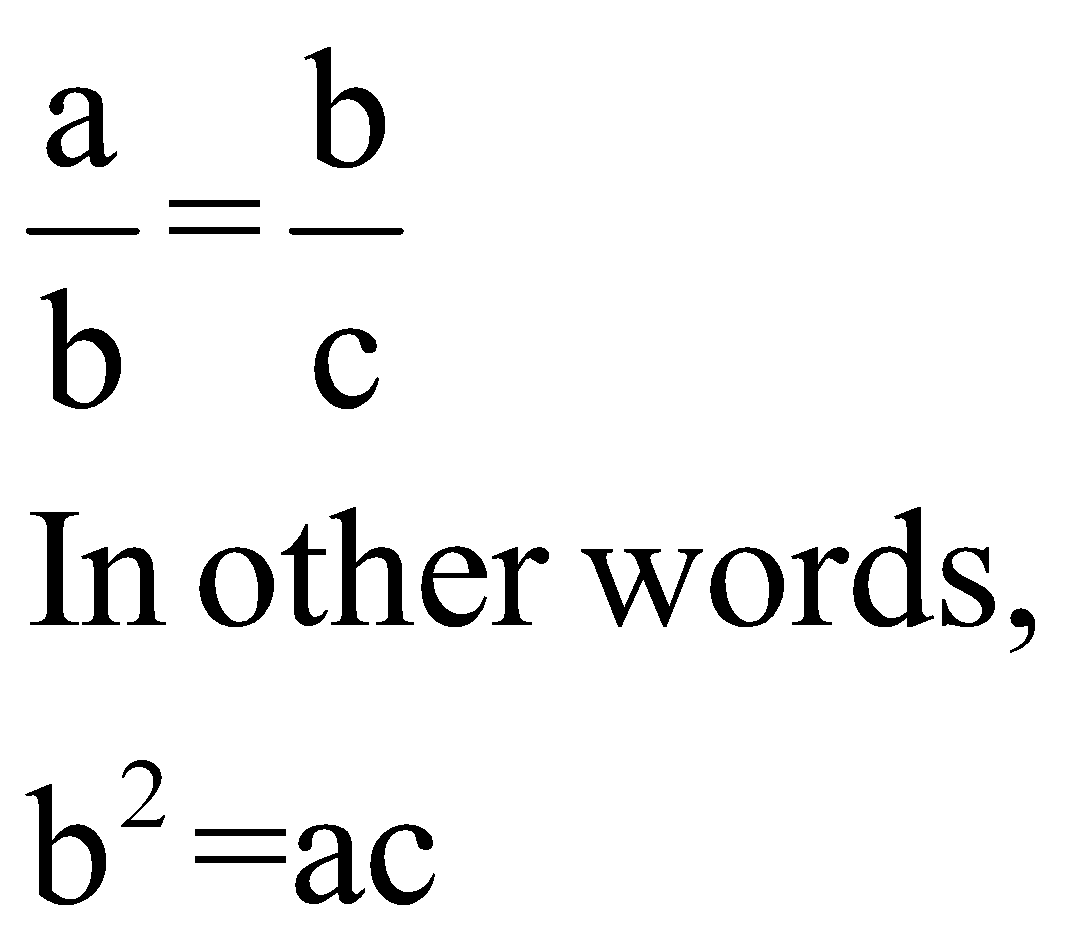
Here, the second quantity (b) is called the mean proportional between the first (a) and the third (c).
The third quantity (c) is called the third proportional to the first and second.
5. Proportion involving more than 4 terms
If ![]() …. then, this can be written as
…. then, this can be written as![]()
Proof:
Let us assume,
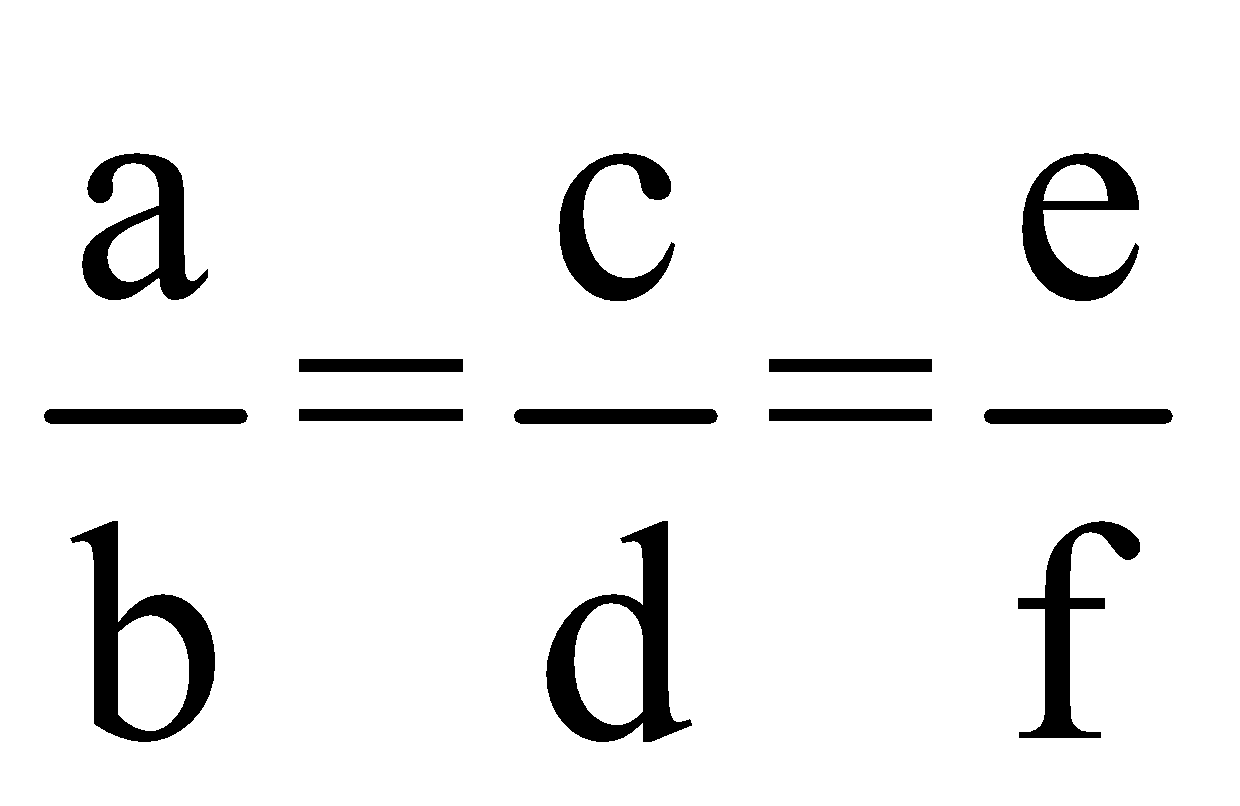 =…….=k
=…….=k
a =bk,c=dk,e=fk=…… … (1)
Now if the result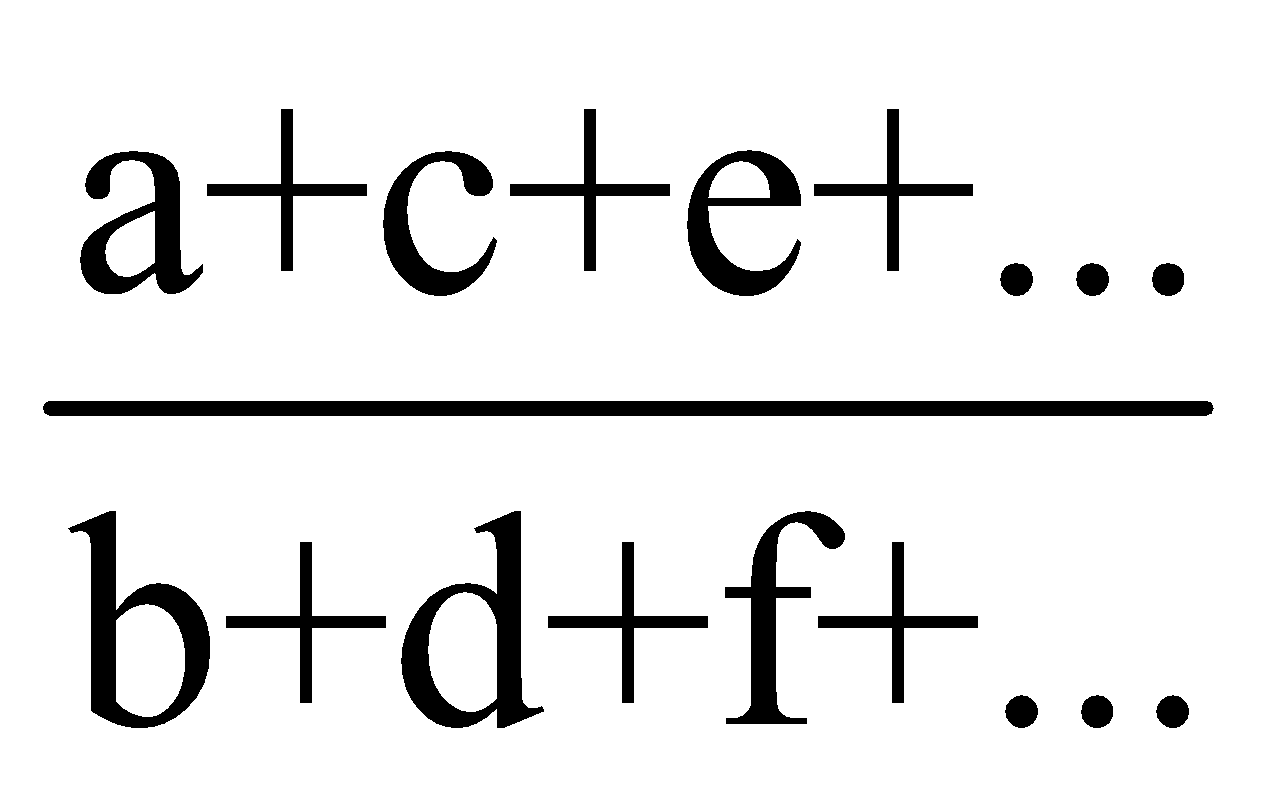 to be true, equation 1 need to satisfy it.
to be true, equation 1 need to satisfy it.
![]() =1
=1
So 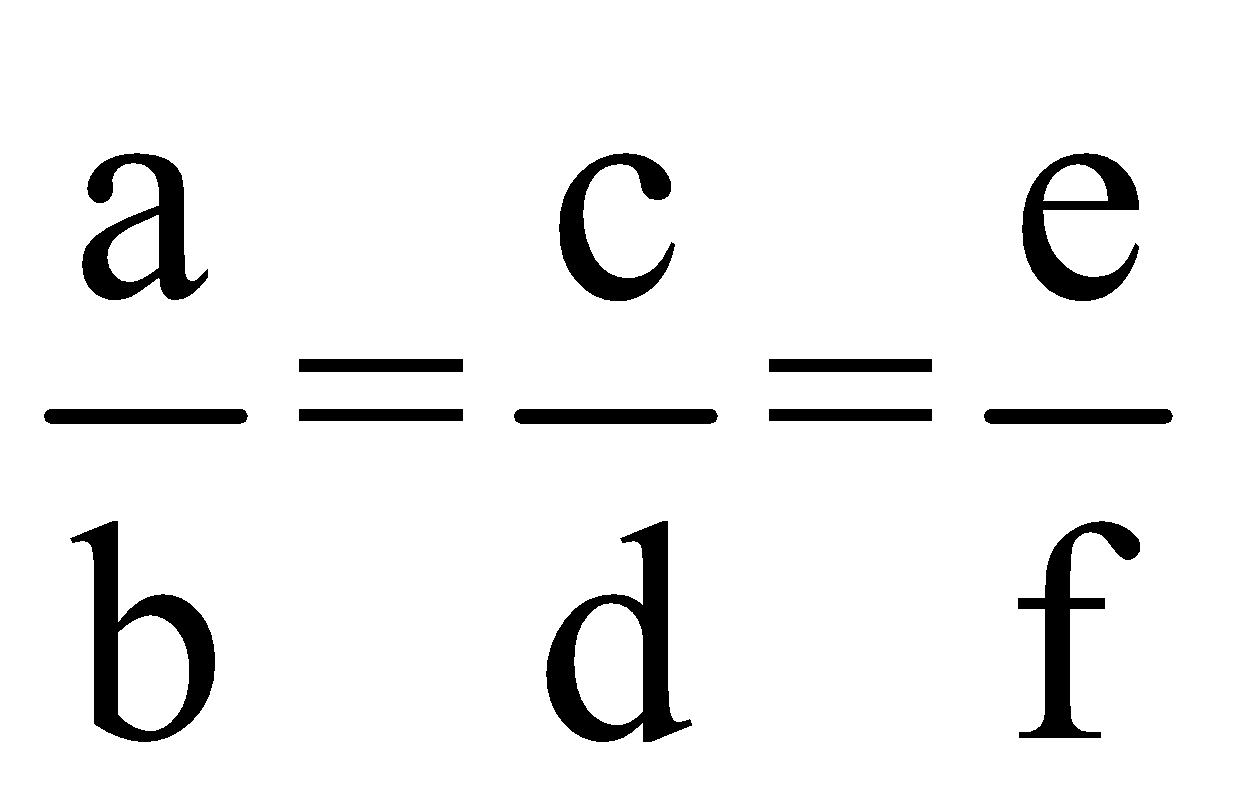 =1.
=1.
To get a firm hold on the above discussed concepts, test yourself on the exercise below:
Exercise:
Question 1: If p: q = r: s = t: u = 2: 3, then (mp + nr + ot): (mq + ns + ou) is equal to:
(1) 1: 3
(2) 1: 2
(3) 2: 3
(4) 3: 2
Answer and Explanation
Solution: (3)
If then each of these ratios is equal to
then each of these ratios is equal to![]()
Here,
![]()
Multiply p and q by m; r and s by n; t and u by o.
![]()
By using the formula
![]()
Question 2: If a: b = c: d = e: f = 1: 2, then (pa + qc + re): (pb + qd + rf) is equal to:
(1) p: (q + r)
(2) (p + q): r
(3) 2: 3
(4) 1: 2
Answer and Explanation
Solution: (4)
If 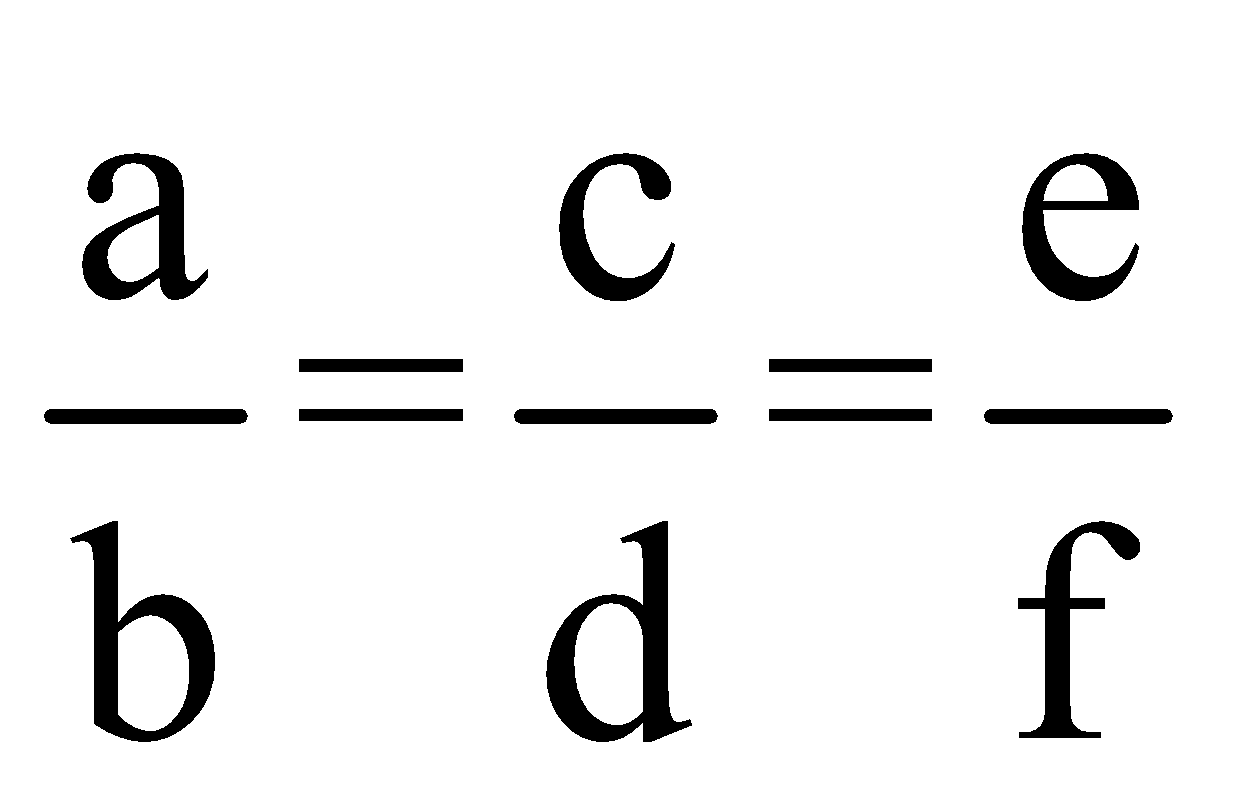 then each of these ratios is equal to
then each of these ratios is equal to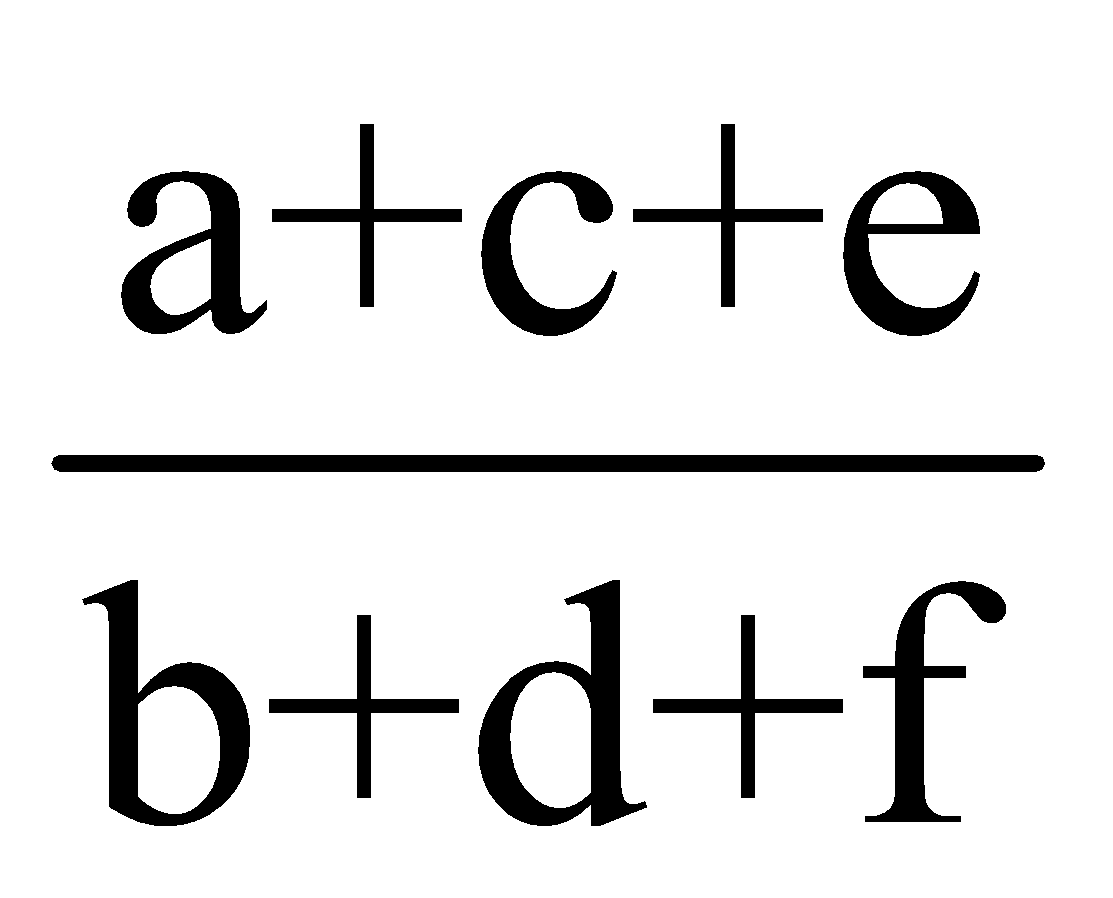
Now![]()
Multiply a and b by p; c and d by q; e and f by r.
![]()
By using the formula
![]()
Question 3: If x: y = 3: 1, then x3 – y3: x3 + y3 =?
(1) 13: 14
(2) 14: 13
(3) 10: 11
(4) 11: 10
Answer and Explanation
Solution: (1)
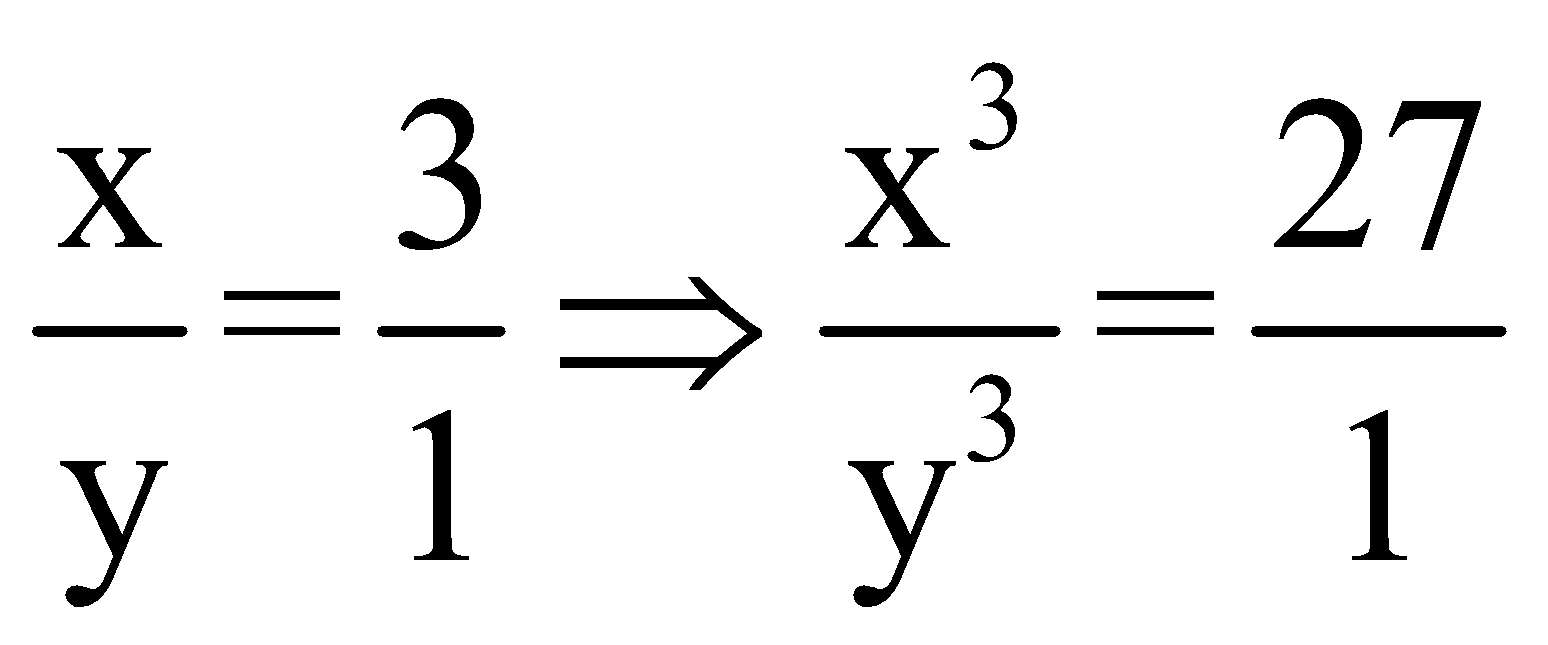
If
![]()
Then by componendo and dividendo
![]()
![]()
Question 4: The fourth proportional to 0.12, 0.21, 8 is:
(1) 8.9
(2) 16
(3) 14
(4) 17
Answer and Explanation
Solution: (3)
Let the fourth proportional be m.
Then, ![]()
or m = 8×![]()
or m = 8×![]()
or m=14
Question 5: If b is the mean proportional of a and c, then (a – b)3: (b – c)3 equals?
(1) a3: c3
(2) b2: c2
(3) a2: c2
(4) a3: b3
Answer and Explanation
Solution: (4)
As per question b is the mean proportional of a and c.
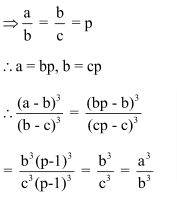
Question 6: If a: b = c: d = e: f = 1: 2, then (3a + 5c +7e): (3b + 5d + 7f) is equal to:
(1) 8: 7
(2) 2: 1
(3) 1: 4
(4) 1: 2
Answer and Explanation
Solution: (4)
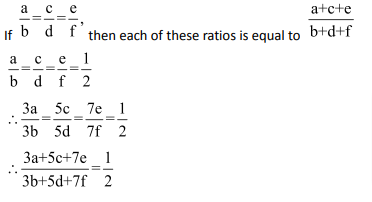
Question 7: If a: (b + c) = 1: 3 and c: (a + b) = 5: 7, then b: (a + c) is equal to?
(1) 1: 2
(2) 2: 3
(3) 1: 3
(4) 2: 1
Answer and Explanation
Solution: (1)

Question 8: The mean proportional between (3 + √2) and (12 –√32) is?
(1)![]()
(2)![]()
(3)6
(4)![]()
Answer and Explanation
Solution: (2)
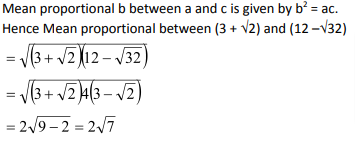
Question 9: If a: b = c: d, then ![]() is not equal to?
is not equal to?
(1)![]()
(2)![]()
(3)![]()
(4)![]()
Answer and Explanation
Solution: (4)
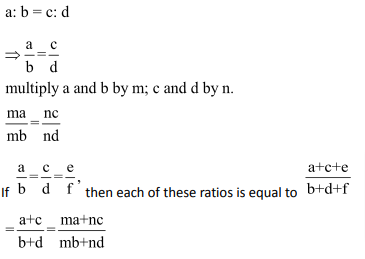
Question 10: If A: B = 3: 4 and B: C = 6: 5, then A: (A + C) is equal to
(1)9: 10
(2) 10: 9
(3) 9: 19
(4) 19: 9
Answer and Explanation
Solution: (3)
![]()
![]()
![]()
![]()
![]()
Question 11: If x: y = 5: 6, then (3x2 – 2y2): (y2 – x2) is?
(1) 7: 6
(2) 11: 3
(3) 3: 11
(4) 6: 7
Answer and Explanation
Solution: (3)
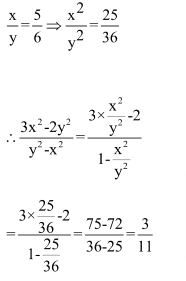
Question 12: If x: y = 3: 4, then 4x + 5y: 5x – 2y is?
(1) 7: 32
(2) 32: 7
(3) 4: 3
(4) 5: 2
Answer and Explanation
Solution: (2)
![]()
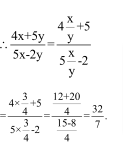
Ratio and Proportion Questions: Problems on Ratio and Proportion you should solve for competitive examination preparation
Welcome to this exercise on Problems on Ratio and Proportion. In this exercise, we build on the basic concepts for Ratio and Proportion. As you prepare for your competitive examinations, you will come across questions on Ratio and Proportion. Such questions need optimized tackling and can be solved













