In the previous lessons on ratio and proportion, we learned the basics and important concepts. Now is the time that we do some practice and apply those formulas, concepts, and tricks to questions. This article consists of various questions for your practice.
EXERCISE:
Question 1: If two times of A is equal to three times of B and equal to four times of C, then A: B: C is?
(1) 2: 3: 4
(2) 3: 4: 2
(3) 4: 6: 3
(4) 6: 4: 3
Answer and Explanation
Solution: (4)
According to the question,
2 A = 3 B = 4C = 12 (say)
A = 6, B = 4 and C = 3
Hence A: B: C = 6: 4: 3.
Question 2: If W1: W2 = 2: 3 and W1: W3 = 1: 2 then W2: W3 is
(1) 3: 4
(2) 4: 3
(3) 2: 3
(4) 4: 5
Answer and Explanation
Solution: (1)
We have W1: W2 = 2: 3
and W1: W3 = 1: 2 = 2: 4
Hence W1: W2: W3 = 2: 3: 4
Hence W2: W3 = 3: 4
Question 3: If 3x = 5y = 4z then x: y: z is equal to?
(1) 9: 12: 16
(2) 20: 12: 15
(3) 15: 10: 9
(4) 8: 5: 3
Answer and Explanation
Solution: (2)
We have 3x = 5y = 4z = 60 (say)
x = 20, y = 12 and z = 15
Hence x: y: z = 20: 12: 15
Question 4: If a and b are rational numbers and
, then a: b is equal to?
(1) –2: 1
(2) 2: 1
(3) √3: 1
(4) –√3: 1
Answer and Explanation
Solution: (2)
We have,
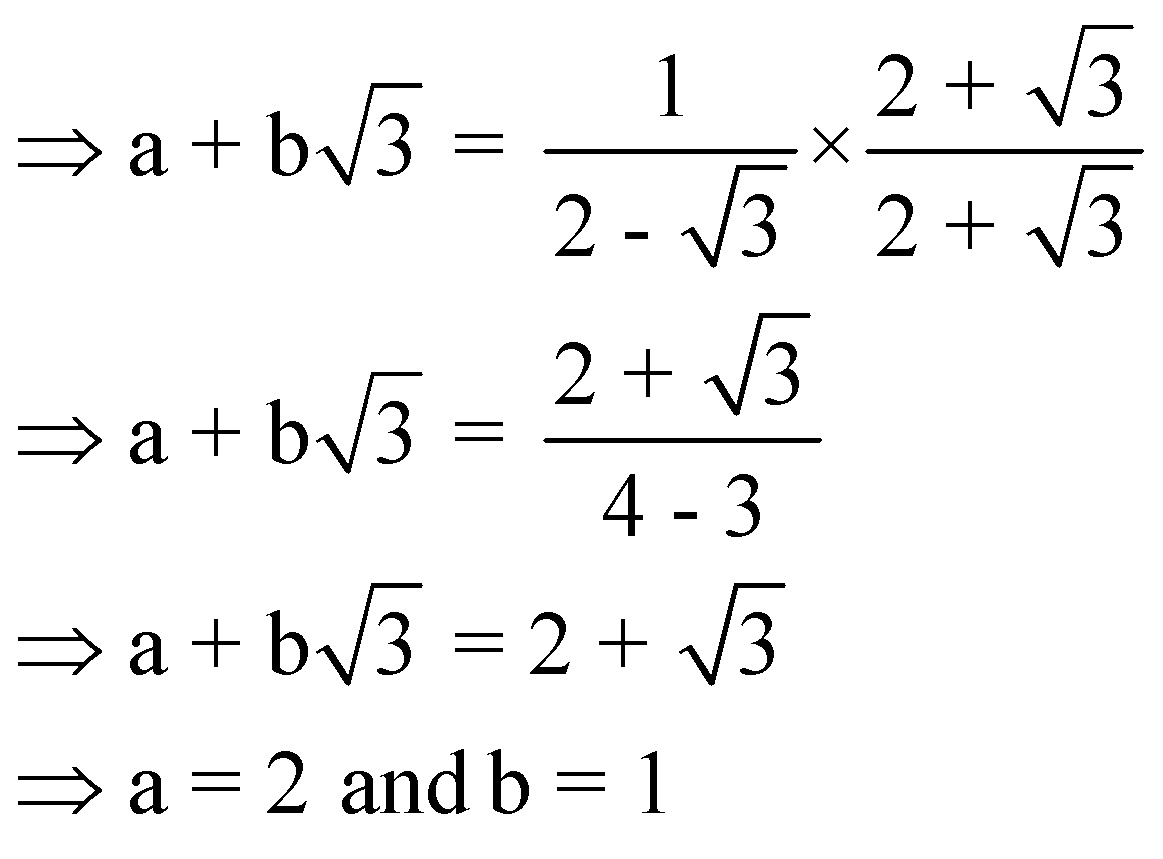
Hence a: b = 2: 1
Question 5: If x: y = 3: 4 and y: z = 3: 4, then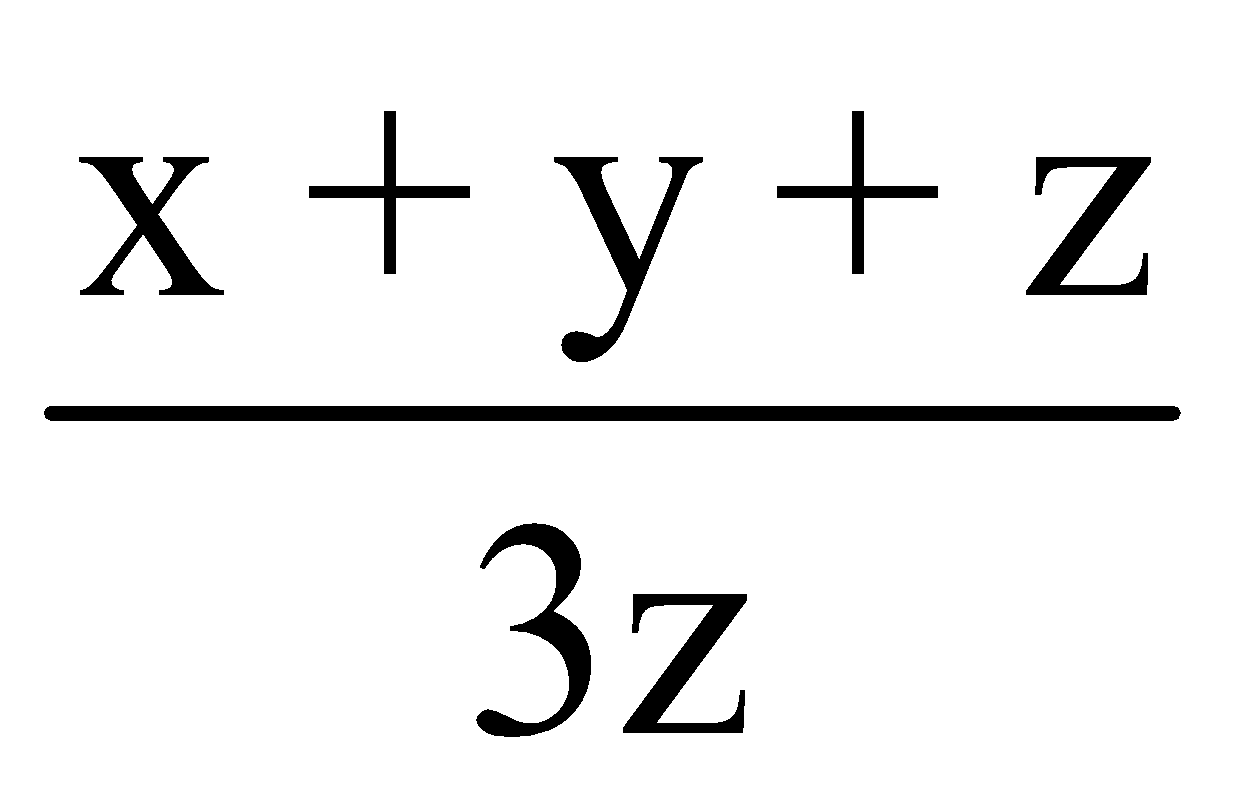 
is equal to
(1) 13/27
(2) 1/2
(3) 73/84
(4) 37/48
Answer and Explanation
Solution: (4)
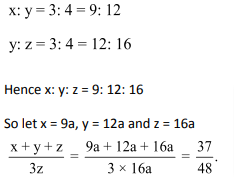
Question 6: To get the ratio p: q (for p ≠ q), what one must add to each term of the ratio x: y?
(1)
(2)
(3)
(4)
Answer and Explanation
Solution: (2)
Let the number to be added = z.
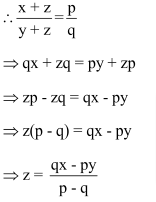
Question 7: If (a + b): (b + c): (c + a) = 6: 7: 8 and (a + b + c) = 14, then the value of c is
(1) 6
(2) 7
(3) 8
(4) 14
Answer and Explanation
Solution: (1)
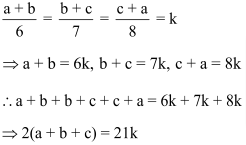
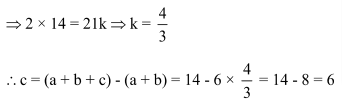
Question 8: The ratio of the incomes of A and B as well as of B and C is 3: 2. If one third of A’s income exceeds one fourth of C’s income by Rs. 1000, what is B’s income?
(1) 3000
(2) 2500
(3) 3500
(4) 4000
Answer and Explanation
Solution: (1)
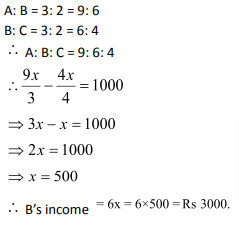
Question 9: There is a ratio of 5: 4 between two numbers. If 40 per cent of the first is 12, then 50% of the second number is:
(1) 12
(2) 24
(3) 18
(4) 20
Answer and Explanation
Solution: (1)
Let the numbers are 5x and 4x.
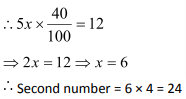
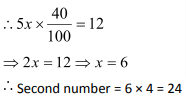
Question 10: The ratio of ages of two students is 3: 2. One is older to the other by 5 years. What is the age of the younger student?
(1) 2 years
(2) 10 years
(3) 5 years
(4) 15 years
Answer and Explanation
Solution: (2)
Let their ages be 3x and 2x, respectively.
Now given that 3x – 2x = 5x = 5
Hence, the age of younger student is 2x = 2 × 5 = 10 years.
Ratio and Proportion Questions: Problems on Ratio and Proportion you should solve for competitive examination preparation
Welcome to this exercise on Problems on Ratio and Proportion. In this exercise, we build on the basic concepts for Ratio and Proportion. As you prepare for your competitive examinations, you will come across questions on Ratio and Proportion. Such questions need optimized tackling and can be solved with ease by using simple tricks and understanding the relationships highlighted in this Ratio and Proportion Questions article. The Ratio and Proportion Questions exercise comes into the picture where it gives you a chance to practice the highlighted and important concepts related to Ratio and Proportion question type.
