Having studied the basics of ratios and proportion, now we will learn another important concept of ratios with the help of some examples.
CONCEPT: DIVIDING A GIVEN QUANTITY IN A GIVEN RATIO
This concept is generally used to divide quantities such as salary, milketc.in a given ratio.
Let us discuss how.
If there is a quantity Q and we need to divide it in ratio of r1 and r2 then
One part will be![]() i.e.,
i.e.,![]()
Second part will be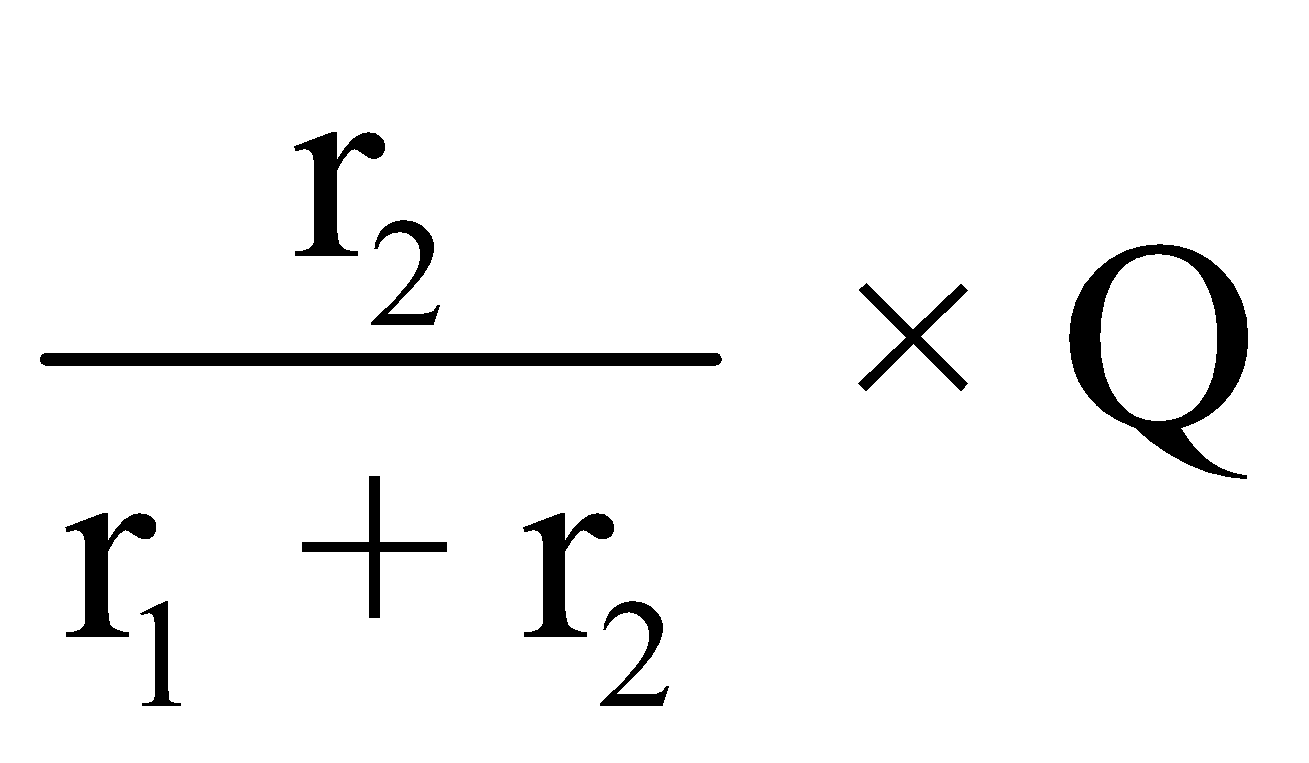 i.e.,
i.e.,![]()
Similar process should be adopted if there are more than 2 ratios given.This will be understood better by taking examples.
We will cover a variety of examples in this section.
Exercise
Question 1: Rs. 6200 divided into three parts proportional to respectively are:
(1) Rs. 3000, Rs. 2000, Rs. 1200
(2) Rs. 3500, Rs. 1500, Rs. 1200
(3) Rs. 2500, Rs. 2000, Rs. 1700
(4) Rs. 2200, Rs. 3000, Rs. 1000
Answer and Explanation
Solution: (1)
Ratio =
![]()
First convert this ratio into simpler one. For that, multiply every term by LCM of all the three denominator values. So, we have the ratios:
![]()
= 15: 10: 6
Hence first part =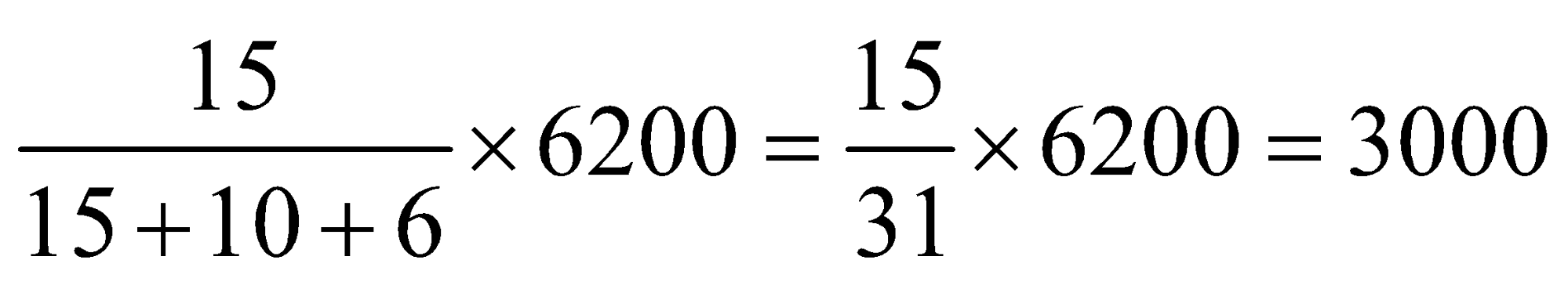
Second Part =![]()
and third part =![]()
Question 2: If Rs. 1000 is divided between A and B in the ratio 3: 2, then A will receive:
(1) Rs. 400
(2) Rs. 500
(3) Rs. 600
(4) Rs. 800
Answer and Explanation
Solution: (3)
The ratio of A and B is 3: 2. Hence A’s share is given by,
![]()
Question 3: Marks of two candidates P and Q are in the ratio of 2: 5. If the marks of P are 120, marks of Q are:
(1) 120
(2) 240
(3) 300
(4) 360
Answer and Explanation
Solution: (3)
Marks of P and Q are in ratio 2: 5. Hence we have,
![]()
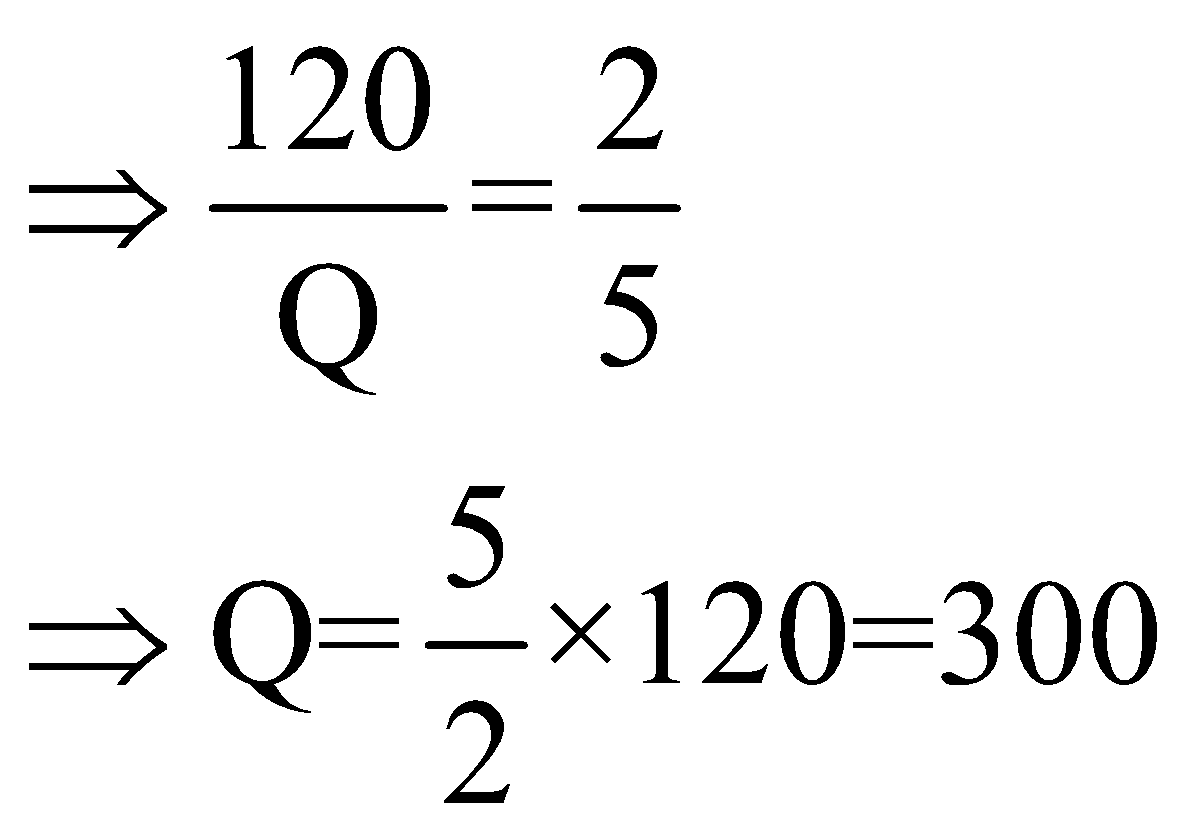
Question 4: Three persons A, B, C whose salaries together amount to Rs. 72000 spend 80, 85 and 75 percent of their salaries respectively. If their savings are in the ratio 8: 9: 20, then A’s salary is?
(1) Rs. 20,000
(2) Rs. 16,000
(3) Rs. 22,000
(4) Rs. 18,000
Answer and Explanation
Solution: (2)
If the salaries of A, B and C Be Rs. x, Rs. y, and Rs. z respectively, then
![]()
![]()
![]()
A’s salary =![]()
Question 5: If 78 is divided into three parts which are in the ratio , the middle part is?
(1) 9![]()
(2) 13
(3) 17![]()
(4) 18![]()
Answer and Explanation
Solution: (3)
The given ratio![]()
Sum of the ratios = 6 + 2 + 1 = 9
![]() Middle part
Middle part![]()
Ratio and Proportion Questions: Problems on Ratio and Proportion you should solve for competitive examination preparation
Welcome to this exercise on Problems on Ratio and Proportion. In this exercise, we build on the basic concepts for Ratio and Proportion. As you prepare for your competitive examinations, you will come across questions on Ratio and Proportion. Such questions need optimized tackling and can be solved with ease by using simple tricks and understanding the relationships highlighted in this Ratio and Proportion Questions article. The Ratio and Proportion Questions examples comes into the picture where it gives you a chance to practice the highlighted and important concepts related to Ratio and Proportion question type.







