CAT 2022 : Ratios With More Than 2 Variables

Till previous chapter of proportion, we have had only 2 variables in questions. What if we have more than 2 variables?
In this lesson, we will discuss the method to solve ratios with more than two variables.
Concept 1: If we have three variables.
If the ratio between first and second quantity is p:q and between second and third quantity is r:sthen what will be the ratio among first,second, and third quantity?
Mathematically if first, second, and third quantities are a,b, and c respectively then:
a:b = p:q
b:c = r:s
a:b:c =?
to solve this, we follow the procedure shown below:

Following the arrows and multiplying the terms we get,
a:b:c =>pr: qr: qs

Concept 2: If we have four variables.
If the ratio between first and second quantity is p:q and between second and third quantity is r:s, between third and fourth is t:uthen what will be the ratio among first,second, third,and fourth quantity?
Mathematically if first, second, third,and fourth quantities are a,b, c, and d respectively then,
a:b = p:q
b:c = r:s
c:d =t:u
a:b:c:d =?
to solve this, we follow this procedure:
(Note: Just like the procedure shown in concept 1, we can extrapolate it to include the 3rd ratio, drawing alternate arrows in upward and downward directions.)

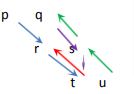
Following the colors and multiplying the variables
a:b:c:d will be =>prt:qrt:qst:qsu
To test both the concepts studied above, solve the exercise given below:

EXERCISE:

Question 1: If A: B = 3: 4, B: C = 5: 7 and C: D = 8: 9 then A: D is equal to

(1) 3: 7

(2) 7: 3

(3) 21: 10

(4) 10: 21

Question 2: If a: b = , b: c = and d: c = then a:b: c: d is

(1)  4: 6: 7: 9

(2)  16: 24: 30: 35

(3)  8: 12: 15: 7

(4)  30: 35: 24: 16

Question 3: If a: b = 5: 7 and c: d = 2a: 3b, then ac: bd is:

(1) 20: 38

(2) 50: 147

(3) 10: 21

(4) 50: 151

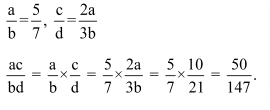
Question 4: If A: B= , B: C = and C: D = , then the ratio A: B: C: D is?

(1)  6: 4: 8: 10

(2)  6: 8: 9: 10

(3)  8: 6: 10: 9

(4)  4: 6: 8: 10

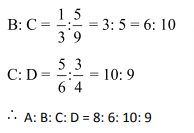
Question 5: If A: B: C = 2: 3: 4, then ratio is equal to

(1) 8: 9: 16

(2) 8: 9: 12

(3) 8: 9: 24

(4) 4: 9: 16

Question 6: If a, b, c are three numbers such that a: b = 3: 4 and b: c = 8: 9, then a: c is equal to?

(1) 1: 3                

(2) 2: 3

(3) 3: 2                

(4) 1: 2

Question7:  If A: B = 2: 3 and B: C = 4: 5, then A: B: C is

(1) 2: 3: 5

(2) 5: 4: 6

(3) 6: 4: 5

(4) 8: 12: 15

Question 8: If A: B = 2: 3, B: C = 2: 4 and C: D = 2: 5, then A: D is equal to:

(1) 2: 15

(2) 2: 5

(3) 1: 5

(4) 3: 5

Question 9: The ratio of A to B is 4: 5 and that of B to C is 2: 3. If A equals 800, then C equals?

(1) 1000

(2) 1200

(3) 1500

(4) 2000

Question 10: If A and B are in the ratio 3: 4, and B and C in the ratio 12: 13, then A and C will be in the ratio:

(1) 3:13

(2) 9: 13

(3) 36: 13

(4) 13: 9

Question 11: If A: B = 3: 2 and B: C = 3: 4 then A: C is equal to?

(1) 1: 2

(2) 2: 1

(3) 8: 9

(4) 9: 8

Question 12: If A: B is 2: 3, B: C is 6: 11, then A: B: C is:

(1) 2: 3: 11

(2) 4: 6: 22

(3) 4: 6: 11

(4) 2: 6: 11

Ratio and Proportion Questions: Problems on Ratio and Proportion you should solve for competitive examination preparation

Welcome to this exercise on Problems on Ratio and Proportion. In this exercise, we build on the basic concepts for Ratio and Proportion. As you prepare for your competitive examinations, you will come across questions on Ratio and Proportion. Such questions need optimized tackling and can be solved with ease by using simple tricks and understanding the relationships highlighted in this Ratio and Proportion Questions article. The Ratio and Proportion Questions exercise comes into the picture where it gives you a chance to practice the highlighted and important concepts related to Ratio and Proportion question type.