In the previous article we have observed speed of an object with respect to an object at rest. But what if both the objects are in motion? In this article we shall get through the concept of Relative Speed.
The relative speed is the speed of one object with respect to the other object and let us understand it with the help of an example.
Consider that you are moving in a car with a speed of 50 km/hr. Another car whose speed is 60 km/hr overtakes you. Now when the other car is overtaking you, you will not experience its speed to be 60 km/hr. You will feel that the car overtook you very slowly. The reason is that you are also moving with 50 km/hr speed. So, what you will experience is the extra speed which the second car has i.e., 10 km/hr. So, for you the other car overtook you at 10km/hr speed. The 10 km/hr speed is the relative speed of the second car with respect to. you.
So, we can say that when two vehicle/ person move in same direction then the relative speed is the difference in their speeds.
Similarly, if two objects move in the opposite direction, then the relative speed is the sum of their speeds.
Now let us take what is the relation of the relative speed with the distance.
- When two vehicles / persons approach each other or move in opposite direction towards each other, then their speeds get added up.
Let us say that there are two cars moving towards each other with speeds 10km/hr and 20km/hr. Let the initial distance between them is 180 km.
![]()
Now we see that if the cars start moving at the same time,then the distance reduced per hr will be 10 + 20 = 30 km. So, the total distance will be travelled in 180/30 = 6 hours.
So,the two cars will cross each other after 6 hours. Hence, we can say that when two objects are moving towards each other, the distance between them is the relative distance and it is covered with the relative speed. So, time taken to cover this distance is given by:
![]()
- When two vehicles/ persons move in same direction then their speed gets subtracted.
Let say two cars start from same point with speeds of 90km/h and 70 km/hr.
Every hour the faster car moves 20 km more than the slower car.Now think this in reverse that after 4th hour, if cars come back then car 1 will be chasing car 2 thus reducing gap by 20 km.
In this case the gap between cars does not depend upon their absolute speed,it depends upon difference between speeds. If we take speed as 100 km/hr and 120 km/hr,gap would still be the same. Hence,
![]()
Solve the exercise given below to get a hold of the concept on Relative Speed.
Exercise:
Question 1: Two trains,100m and 200 m in length respectively are running in opposite directions, one at 10 km/hr speed another at 8 km/hr. In what time will they be completely clear of each other from the moment they meet.
Answer and Explanation
The distance travelled by the trains will be equal to sum of their length = 100 + 200 = 300m
Relative speed = 10 + 8 = 18km/hr. =
![]()
![]()
Question 2: Two trains, 100m and 200 m in length respectively are running in same directions, one at 10 km/hr speed another at 8 km/hr. In what time will they be completely clear of each other from the moment they meet.
Answer and Explanation
The distance travelled by the trains will be equal to sum of their length = 100 + 200 = 300m
Relative speed = 10-8 = 2 km/hr. =
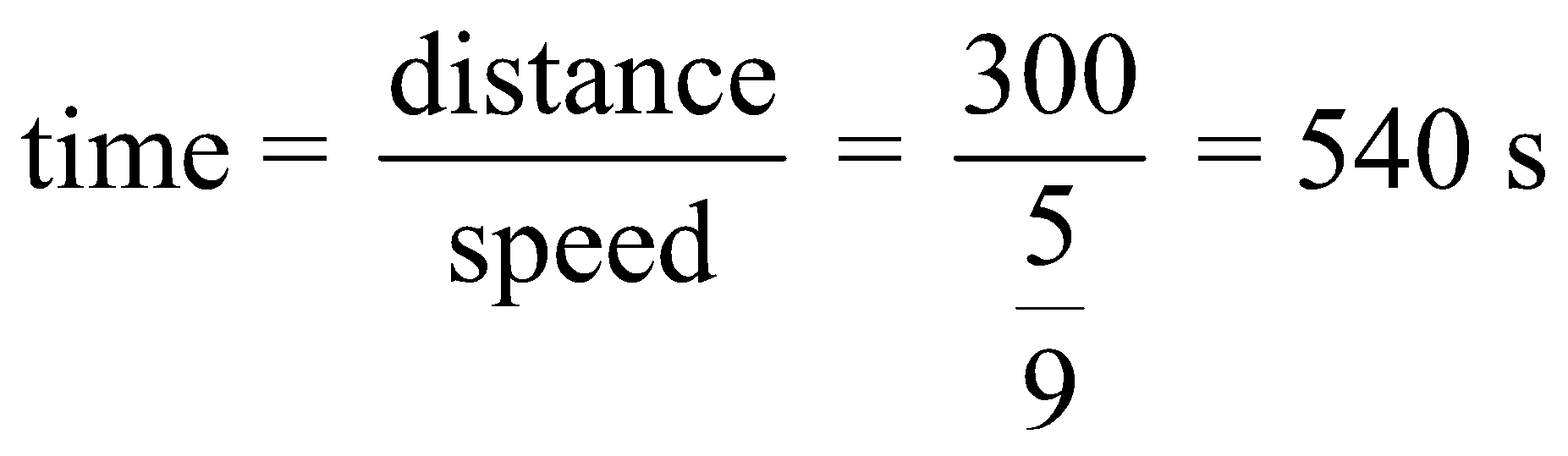
![]()
Question 3: A train 120 m in length,travels at 50km/hr.In what time will it pass a man who is walking at 4 km an hour (a) in opposite direction (b) in the same direction.
Answer and Explanation
When the train and the man are moving in opposite direction.
Relative speed= 50+4 = 54 km/hr = 15 m/s


Question 4: Two trains are moving in the same direction at 30km/hr and 12 km/hr.The faster train crosses a man sitting in the slower train in10s.Find the length of faster train.
Answer and Explanation
The distance covered by faster train is basically equal to its own length.
Time taken = 10s
So, the length of the faster train = 10 × 5 = 50 m.
Question 5: A train running at 12km/hr takes 18 second to pass a platform. Then it takes 6 seconds to pass a man walking at 6 km/hr in the opposite direction.Find the length of train and platform.
Answer and Explanation
Let the length of the train is ‘x’ meter and that of the platform is ‘y’ meter.
![]()
Time taken to cross platform = 18second
![]()
Now when it crosses the man it travels a distance equal to its own length.
Relative speed of train and man =
![]()
So, x = 5 × 6 = 30 m
Hence y = 60 – 30 = 30m
Hence the length of the train and the platform is 30 m each.
Question 6: Two trains starts at the same time from point P and Q towards each other at the rate of 40km/hr and 60 km/hr. When they meet, they found that one train has travelled 120km more than other.Find the distance between P and Q.
Answer and Explanation
Suppose that the train at Q travelled more distance.
=> x-y=120km … (1)
Time taken by train at P to reach at meeting point = Time taken by train at Q to reach at meeting point
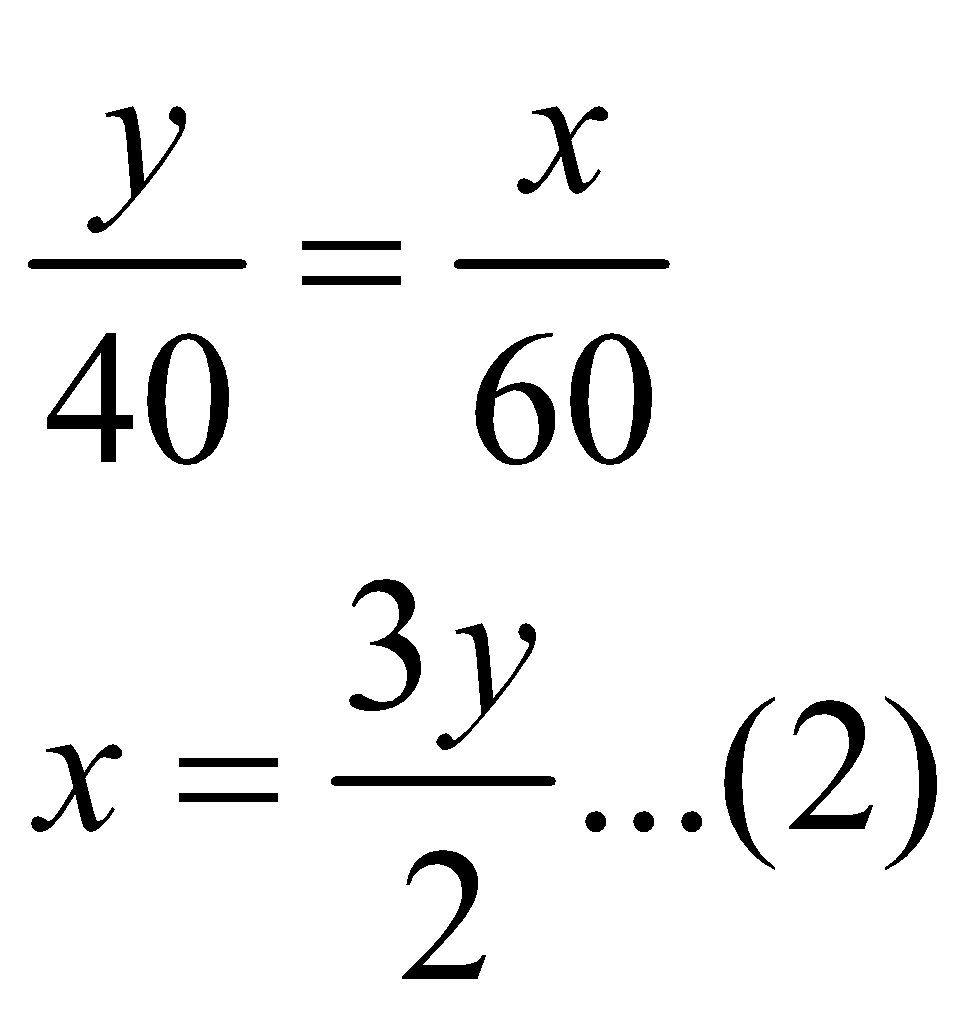
So, from equation (i), we have:
![]()
So, x = 240 + 120 = 360 km
Total distance= 240+360=600km
Speed Time Distance Questions: Problems on Speed Time Distance you should solve for competitive examination preparation
Welcome to this exercise on Speed Time Distance. In this exercise, we build on the basic concepts for Speed Time Distance and focus on relative speed. As you prepare for your competitive examinations, you will come across questions on Speed Time Distance with focus on relative speed. Such questions based on relative speed need optimized tackling and can be solved with ease by using simple tricks and understanding the relationships highlighted in this Speed Time Distance Questions article. The Speed Time Distance Questions exercise comes into the picture where it gives you a chance to practice the highlighted and important concepts related to this Speed Time Distance and relative speed question type.







