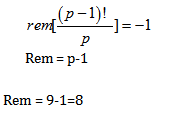In the previous article, we discussed 2 ways to find remainders. Now, we’ll look at more methods to find remainders.
In this article, we will discuss 3 important theorems that make finding remainders very easy and simple.
Method of finding Remainder by Euler’s, Fermat’s little theorem , Wilson’s theorem
- Euler’s Theorem:
According to the Euler’s theorem, if 
is divided by f where ( N and f are co-prime to each other and 
is = total co-primes less than f ) , remainder will always be 1 .we can write it as follows
Solution:
Step 1:
Solution:
Step 1:
Example: Find the remainder of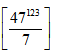 
Solution:
Since 7 is a prime number hence from Fermat’s little theorem .
Solution:
Try out some more questions based on this concept so as to get a good hold of this topic.
EXERCISE:
Question 1. Find the remainder of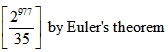 
(1) 32
(2) 16
(3) 8
(4) 24
Answer and Explanation
Solution: option 1
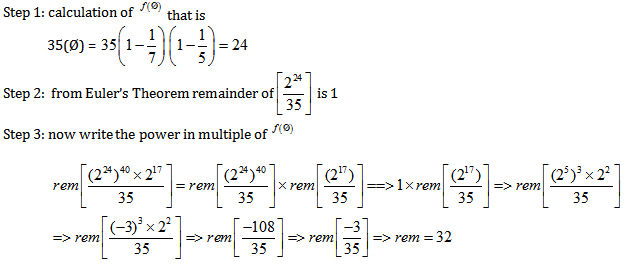
Question 2 . Find remainder of 
(1) 32
(2) 16
(3) 8
(4) 24
Answer and Explanation
Solution: option 2
Question 3. Find remainder of 
(1)122
(2)16
(3)61
(4)37
Answer and Explanation
Solution: option 3
Question 4. Find the remainder of 
(1) 4
(2) 3
(3) 1
(4) 2
Answer and Explanation
Solution: option 3
Question 5. Find the remainder of 
(1) 1
(2) 16
(3) 4
(4) 8
Answer and Explanation
Solution: option 4
