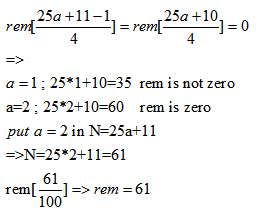This article further covers the ways to calculate remainders.
Remainder Theorem:
Remainder theorem states that when a polynomial function f(x) is divided by (x –a) where a is a constant, it will give us a remainder f(a).
Remainder of ![]()
Let us understand this with the help of some examples.
Example: Find the remainder of 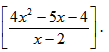 Solution:
Solution:
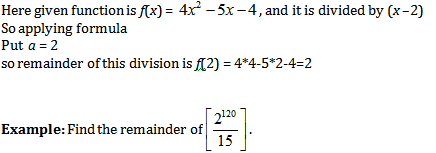
Solution:
Method 1:
Here, note that numerator is in the form of powers of 2 hence we have to convert the denominator also in the form of powers of 2. Here denominator 15 = 24 –1
Now denominator is in the form of 24, so we can write numerator also in the form of 24.
2120 = (24)30. Now if take 24 = x
then numerator => x30
denominator = x –1.
Now by applying remainder theorem concept
a = 1 so remainder is f(a) = (1)30 = 1.
Chinese Remainder Theorem:
Chinese theorem is used when we have a big composite number in denominator and complex power in numerator.
Let us understand this with the help of some examples:
Case 1: When remainder obtained by both numbers is equal
Example: Find the remainder of ![]()
Solution:
Step 1:
Write the denominator as product of two coprimes
In this case 15 = 5 * 3
And dedude remainder for respective factor
Step 2:

Case 2: When remainders obtained by both numbers are unequal
Example: Find the remainder of 
Solution:
Step 1:

Step 2:
Now we need values of a and b for that N is same


Try out some more questions based on this concept so as to get a good hold of this topic.
EXERCISE:
Question 1. Find the remainder of .
(1) 22
(2) -22
(3) 11
(4) 0
Answer and Explanation
Solution: Option 2
Here given function is f(x) = 3×3 –3x –4, and it is divided by (x + 2) hence here a = –2, so remainder of this division if f(–2) = 3 × (–2)3 –3 × (–2) –4 = –24 + 6–4 = –22
Question 2. Find remainder of .
(1) 12
(2) 32
(3) 162
(4) 0
Answer and Explanation
Solution: Option 3
Step 1:
Split 100 into two coprimes
Since 100 = 25 × 4 hence we will 1st find remainder of
Step 2:

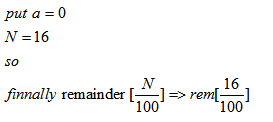
Question 3. Find remainder of ![]()
(1) 37
(2) 52
(3) 16
(4) 61
Answer and Explanation
Solution: Option 4
Step 1 :
Split 100 into two coprimes
Since 100 = 25 × 4 hence we will 1st find remainder of
Step 2:-

Step 3 :
We need to find value of a for that