This is the final article covering some more handy methods to find remainders, out of which the most comfortable method can be chosen to save time dealing with remainder questions.
Method 1:
Example: Suppose we have two numbers “a” and “b”. If “a” is in form of 7n +4 and “b” is in form of 7m+1.
Addition
Find remainder when a+b is divided by 7.
Given a = 7n +4
and b = 7m + 1
So when we add them we will have a +b = 7n + 7m + 4 + 1 = 7 (n + m) + 5
That means we have a multiple of 7 and a remainder 5, because five is smaller than the 7. So it cannot be divided further and hence this 5 is our remainder.
Difference
What will be the remainder when a – b is divided by 7?
Given a = 7n +4
and b = 7m + 1
So when we subtract them we will have a – b= (7n +4) – (7m + 1)
= 7(n – m ) + 4 – 1
= 7(n – m ) + 3.
That means we will have a multiple of 7 with addition of 3 and because three
is smaller than the 7 so it cannot be divided further and hence this 3 is our remainder .
Multiplication
What will be the remainder when a x b is divided by 7?
Given: a = 7n +4
and b = 7m + 1
So when we multiply them we will have a x b = (7n +4) x (7m + 1)
= 7n(7m + 1) + 4(7m + 1)
= 49nm + 7n + 28nm + 4. Here we can see that each and every number is a multiple of 7 except 4. Hence this 4 is our remainder.
Some Important Properties of Prime Numbers
- Any single digit number written (P – 1) times is divisible by P, where P is a prime number > 5.
Example: Find the remainder of ![]()
Solution:
11 is a prime number. Any digit repeated (11-1) times or multiple of 10 times must be divisible by 11.
Now, in the given question, digit 7 is repeated 99 times hence it must be divisible by 11 .so remainder = 0
Example: Find the remainder of ![]()
Solution:
19 is a prime number and any digit repeated (19-1) times or multiple of 18 times must be divisible by 19.

Method 2: Cancelation
Cancellation is applied to make the calculations easier. First we cancel out the common factors and then multiply those factors back after finding remainders.
Example: Find the remainder of ![]()
Solution:
Method 1:
Since common factor is 9 = 32

Try out some more questions based on this concept so as to get a good hold of this topic.
EXERCISE:
Question 1. What is the remainder when 111 + 68 + 48 is divided by 11?
a) 5
b) 7
c) 9
d) None
Answer and Explanation
Solution: option b 111 leaves remainder 1 when divided by 11
68 leaves remainder 2 when divided by 11
48 leaves remainder 4 when divided by 11
Thus111 + 68 + 48 leaves remainder 1+2+4 =7 when divided by 11
Question 2. Find the remainder of 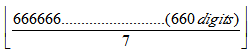
a)5
b)0
c)9
d)None
Answer and Explanation
7 is a prime number. Any digit repeated (7-1)=6 times or multiple of 6 times must be divisible by 7.
Now, in the given question digit 6 is repeated 660 times hence it must be divisible by 7, so remainder = 0
Question 3. ![]()
a) 25
b) 0
c) 50
d) None
Answer and Explanation
Solution: option a








