So far we have been introduced to remainders. In mathematics section of any exam, questions on remainder are quite common. Therefore, you should know this topic in and out. So, let’s get started.
Various Ways To Calculate Remainders:
- Method of finding Remainder by cyclicity.
- Method of finding Remainder by negative remainder concept
- Method of finding Remainder by Euler’s, Fermat’s little theorem , Wilson’s theorem
- Method of finding Remainder: “Remainder theorem” ( in case of polynomials )
- Method of finding Remainder: Chinese theorem
- Some important formats to find remainders
In this article, we’ll study the first two ways to find remainders of a given number.
- Method to find Remainder by Cyclicity:
Remainders repeat themselves in the same pattern after a certain length. This helps in solving questions quickly.
Let us understand it with the help of an example:
Example: Find the remainder of ![]()
Solution:
Step 1:
Check what pattern is made by remainders of this particular set of divisor and dividend.
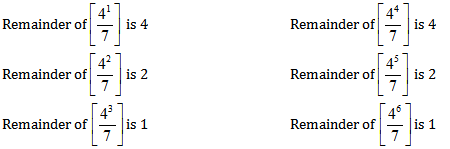

Step 2:
Now write the power in the form of 3n+ k
10 = 3*3+1

Solution:
Step 1 :
Check what pattern is made by remainders of this particular set of divisor and dividend .
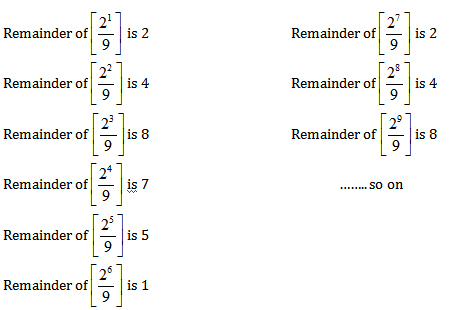
Now we know the cycle is of 6
Step 2 :
Now write the power in the form of 6n+ k
500 = 6*83+2
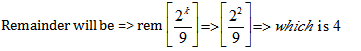
Given below are few tips based on the above method,
Tooltips:
![]()
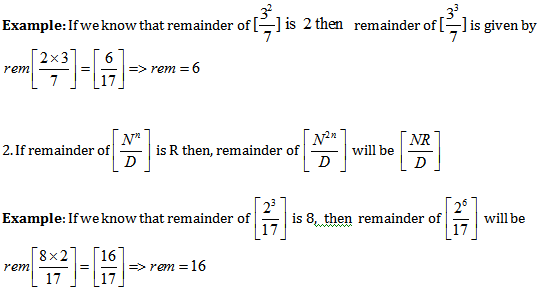
- To find remainder with the help of Negative Remainder concept:
Concept of negative remainder is very useful to reduce calculation. Let us understand the negative remainder and its use.
If we have to divide 120 by 11 then remainder obtained is 10
Dividend = divisor * quotient + remainder
N = D*Q+R
120 = 11*10+10
Or in other way we can write
120 = 11*11 – 1 hence remainder is (–1).
So R can be either 10 or (-1)
So we can say that when a number N is divided by D then remainder obtained it R which can also be written as R’= (R -D )
Let us see the use of negative remainder concept:
Example: Find the remainder of ![]()
Solution:
Method 1:

R = 10
R’ = R-D=10-15= (-5)
443 = 15*29+8
R = 8
R’ = R-D=8-15= (-7)
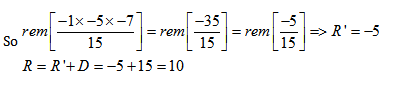
{This method looks a little lengthy, but with a little practice it can be mastered and used everywhere}
Example: Find the remainder of ![]() Solution:
Solution:
By using negative remainder concept:

EXERCISE:
Question 1. Find the remainder of
(1) 5
(2) 7
(3) 8
(4) 4
Answer and Explanation
Solution: Option 1
Step 1: Check what pattern is made by remainders of this particular set of divisor and dividend.

Hence, we have 6 points in cycle.
To find the required remainder we will divide the given power/exponent by 6 in this case 150/6 has remainder zero
Hence 6th point of the cycle will give us the required remainder
![]()
Question 2. Find the remainder of ![]() .
.
(1) 5
(2) 7
(3) 8
(4) 4
Answer and Explanation
Solution: Option 3
By using negative remainder concept:-

Question 3. Find the remainder when 79644 is divided by 9.
(1) 5
(2) 7
(3) 1
(4) 4
Answer and Explanation
Solution: option 4
We will do this question step by step
Step 1: We divide 79 with 9 to get remainder as 7.
Step 2: Here in the question 79 is multiplied by itself 644 times. Now understand every time when we will divide 79 with 9 the remainder will be 7.
Step 3: Hence we can say finding remainder of 79644 is equivalent to finding remainder of 7644 when divided by 9.
So we start observing powers of 7.
72 gives remainder 4.
73 gives remainder 1.
Hence after 3rd power remainders will start repeating. So we have a cycle of 3 and thus we divide 644 by 3 i.e. 644= 3(214) + 2
Hence 7 644 -> 7 3(214) + 2 -> 73(214) .72-> 1.4 = 4 (As 73 gives remainder 1 and 72 gives remainder 4)
Hence the remainder of 79644 when divided by 9 is 4.
Question 4. Find the remainder when 47123 is divided by 7.
(1) 4
(2) 6
(3) 2
(4) 3
Answer and Explanation
Solution: Option 2
We will do this question step by step
Step 1: We divide 47 with 7 to get remainder as 5.
Step 2: Here in the question 47 is multiplied by itself 123 times. Now understand every time when we will divide 47 with 7 the remainder will be 5.
Step 3: Hence we can say finding remainder of 47123 is equivalent to finding remainder of 5123 when divided by 7.
So we start observing powers of 5.
52 gives remainder 4.
53 gives remainder 6.
54 gives remainder 2.
55 gives remainder 3.
56 gives remainder 1.
Hence after 6th power remainders will start repeating. So we have a cycle of 6 and thus we divide 123 by 6 i.e. 123= 6(20) + 3
Hence 5 123-> 5 6(20) +3 -> 5 6(20) .5 3 -> 1.6 =6 (As 56 gives remainder 1 and 53 gives remainder 6)
Hence the remainder of 47123 when divided by 7 is 6.
Question 5. Find the remainder when 257 is divided by 3?
a) 0
b) 1
c) 2
d) None of these
Answer and Explanation
Solution: Option c
So we start observing powers of 2.
21 gives remainder 2.
22 gives remainder 1.
23 gives remainder 2.
24 gives remainder 1.
Hence we can observe odd power of 2 gives remainder 2 and even power gives remainder 1.
Hence 257 will give remainder 2 when divided by 3.







