The chapter of speed timedistance is one of the most important chapter in arithmetic.
We know that there is very basic relation between speed and distance. E.g., if I say that I am travelling at 60 km/hr and I had travelled for 3 hours then it is not difficult to understand that I covered 60 × 3 = 180 kms. This is the very basic relation between speed, time and distance which will form the backbone of this chapter. The entire concept revolves around this relation:
Distance = Speed × Time
From here we can also get 
or
Units of Speed, Time, and Distance:
The units used to measure the distance, time and speed are very important while solving the questions of this topic. We need to be careful about the units used. Normally there are two types of units used.
- If the distance is measured in kilometers, the time is measured in hours then the speed is measured in km/hr.
- If the distance is measured in meters, the time is measured in seconds then the speed is measured in m/sec.
There is a direct relation in these two types of units.
We know that
Hence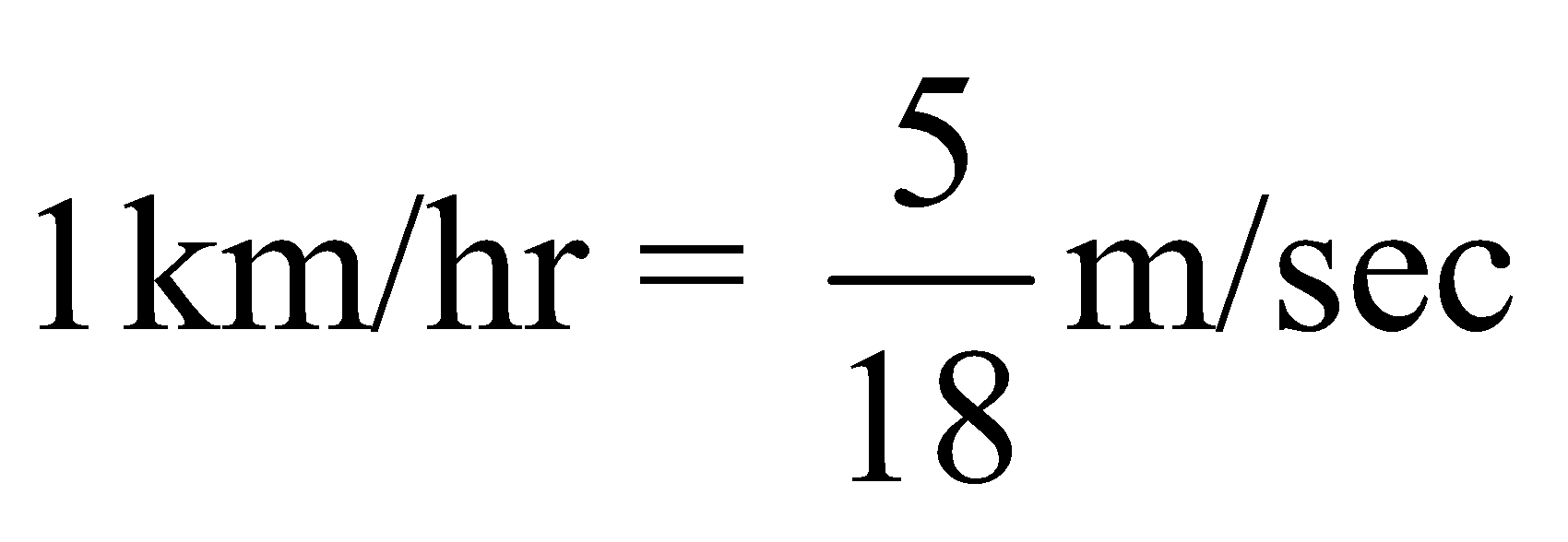
or 
So, in the problems where we must convert the units from km/hr to m/sec or vice versa, we use the above relations.
Example: Let the speed of an object is given to be 108km/hr. Its speed in m/sec will be?
Solution: 
Example: if the speed of an object is 40 m/sec, then its speed in km/hr will be?
Solution:
Average Speed:
The average speed of an object is the ratio of the total distance travelled and the total time taken. Mathematically, 
Example: If a person travels 250 km in 4 hours, then next 300 km in 6 hours and then the next 150 km in 4 hours, then what his average speed?
Solution: The average speed =
There are two special cases for average speed:
Case I: When the time interval is same:
Let a person travels at a speed of 60km/hr in first hour, his speed in the next hour is 80 km/hr and in the third hour is 140km/hr. Then the distance travelled by him in the first hour is 60km, in the next hour is 80 km and in the third hour is 140 km, so his average speed =
Now in this case the average speed is simply the average of the given speeds.
Case II: If the distance travelled is same:
Let a person travels two distances AB and BC where AB = BC = x km. Let his speed during his journey from A to B is a km/hr and from B to C is b km/hr. In this case the
Average speed =
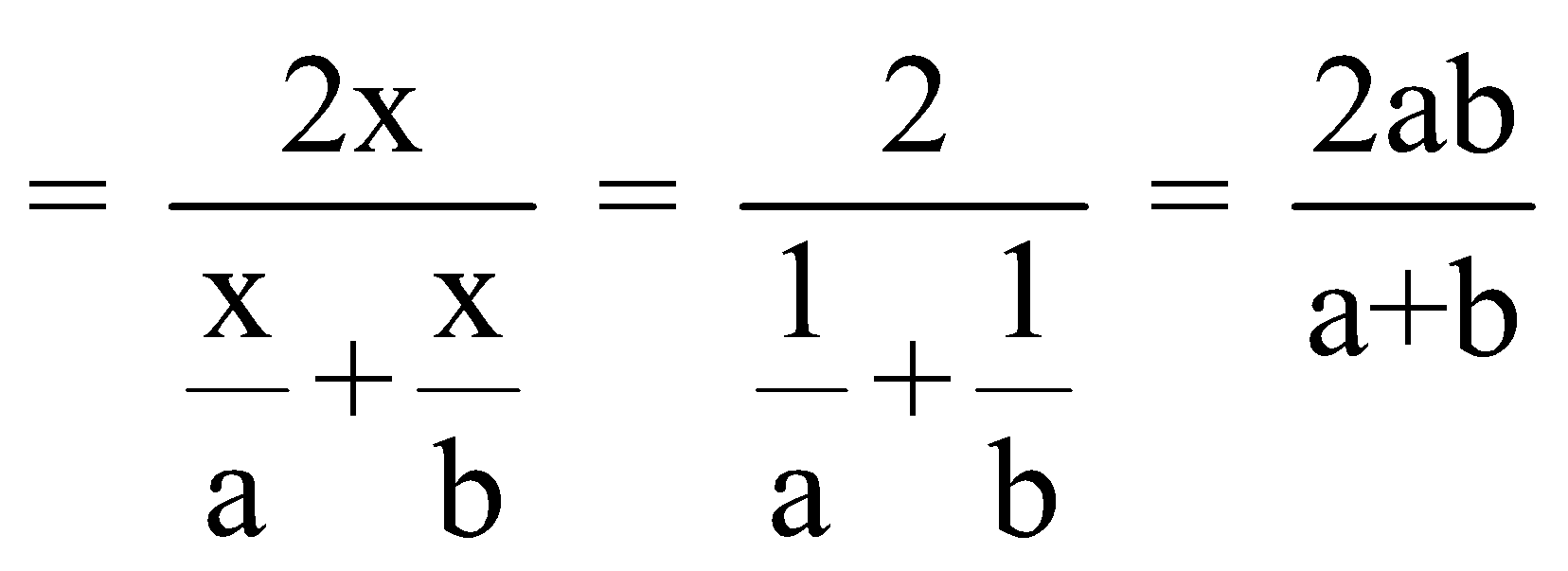
Example: A person travels first half of his journey at 40km/hr. and the next half at 50 km/hr. Find his average speed.
Solution: Since we are given two halves of the journey, so the distance travelled in both the cases is same. Hence the average speed =
To get a deep understanding of the concept solve the exercise below:
Exercise:
Question 1: A train is travelling at the rate of 45 km/hr. How many seconds,will it take to cover a distance of4/5 km?
(1) 36
(2) 64
(3) 90
(4) 120
Answer and Explanation
Solution: (2)
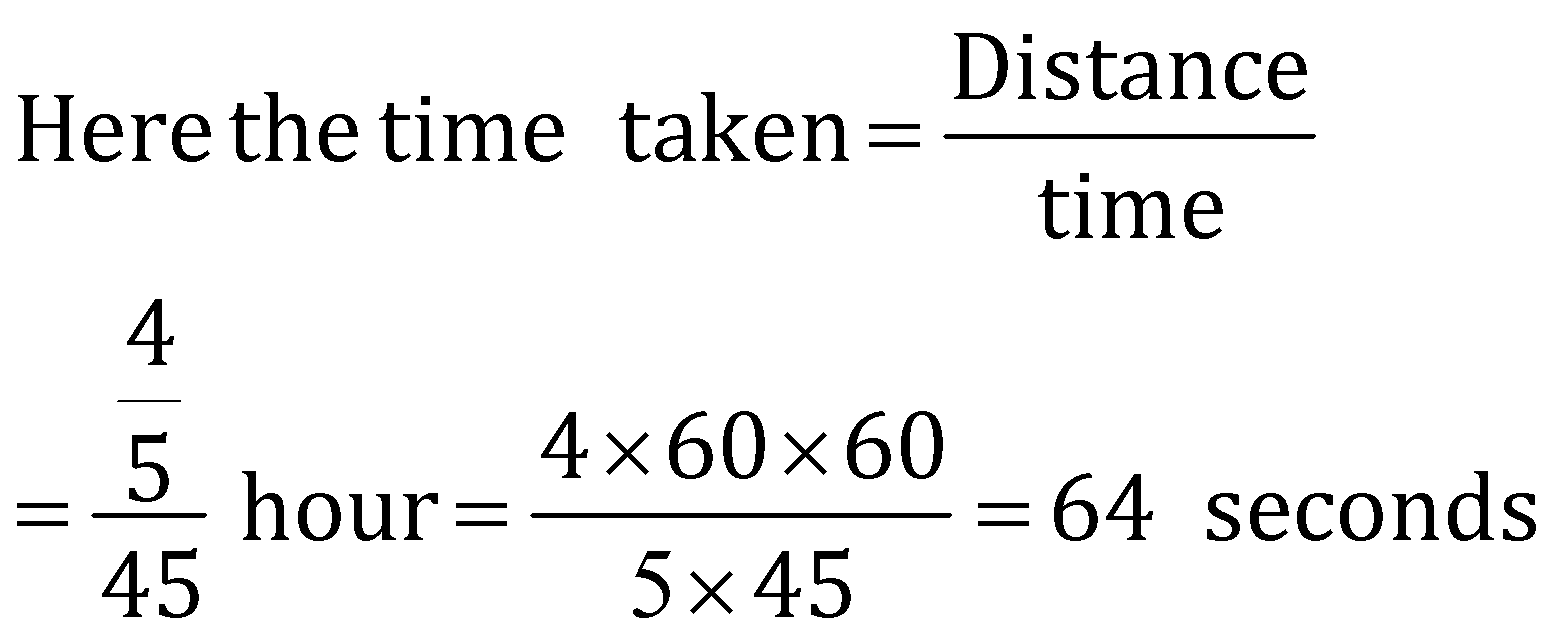
Question 4: A man travelled a certain distance by train at the rate of 25 km/h. And walked back at the rate of 4 km/h. If the whole journey took 5 hours 48 minutes, the distance was?
(1) 25 km
(2) 30 km
(3) 20 km
(4) 15 km
Answer and Explanation
Solution: (3)
Let the distance be x km.
Total time = 5 hours 48 minutes
Question 3: Ram arrives at a Bank 15 minutes earlier than scheduled time if he drives his car at 42 km/h. If he drives car at 35 km/h he arrives 5 minutes late. The distance of the Bank, from his starting-point is?
(1) 70 km
(2) 210 km
(3) 72 km
(4) 60 km
Answer and Explanation
Solution: (1)
Let the required distance be x km.
Difference of time = 15 + 5 = 20 minutes 
hour.
According to the question,
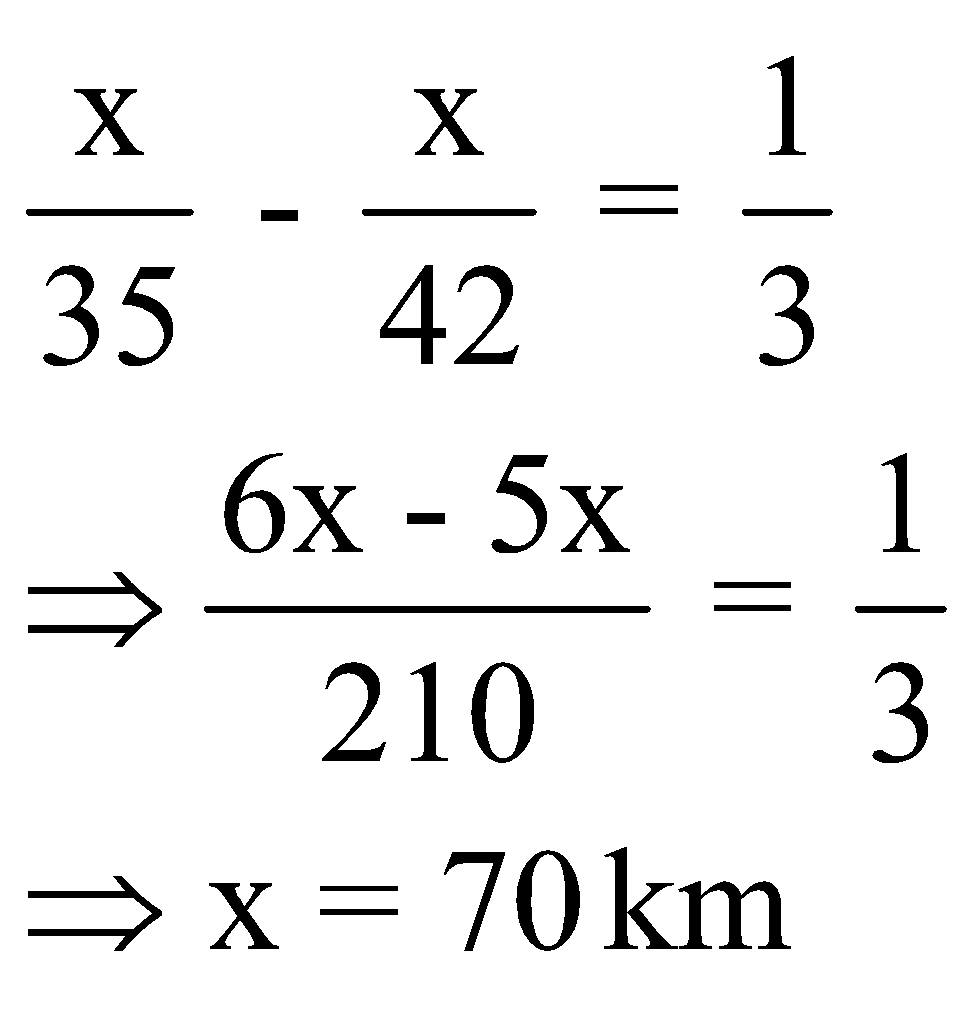
Question 4: A and B started at the same time from the same place for a certain destination. B walking at
of A’s speed reached the destination 1 hour 15 minutes after A. B reached the destination in?
(1) 6 hours 45 minutes
(2) 7 hours 15 minutes
(3) 7 hours 30 minutes
(4) 8 hours 15 minutes
Answer and Explanation
Solution: (3)
Time taken by A – Time taken by B =
x Time taken by B = 1 hour 15 minutes
∴Time taken by B = 1 hour 15 minutes × 6 = 7 hours 30 minutes
Question 5: Ravi and Ajay start simultaneously from a place A towards B, 60 km apart. Ravi’s speed is 4 km/hr less than that of Ajay. Ajay, after reaching B, turns back and meets Ravi at a places 12 km away from B. Ravi’s speed is?
(1) 12 km/hr
(2) 10 km/hr
(3) 8 km/hr
(4) 6 km/hr
Answer and Explanation
Solution: (3)
Let the speed of Ravi be s kmph.
∴Ajay’s speed = (s +4) kmph
Distance covered by Ajay = 60 +12 = 72 km
Distance covered by Ravi = 60 – 12 = 48 km.
According to the question,
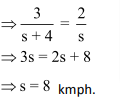
Speed Time Distance Questions: Problems on Speed Time Distance you should solve for competitive examination preparation
Welcome to this exercise on Speed Time Distance. In this exercise, we build on the basic concepts for Speed Time Distance. As you prepare for your competitive examinations, you will come across questions on Speed Time Distance. Such questions need optimized tackling and can be solved with ease by using simple tricks and understanding the relationships highlighted in this Speed Time Distance Questions article. The Speed Time Distance Questions exercise comes into the picture where it gives you a chance to practice the highlighted and important concepts related to the Speed Time Distance question type.
