In the previous article, we discussed squares, its importance and properties related to squares. But what are square roots? Let us learn about square roots.
Definition: The square root of a number x is that number which when multiplied by itself gives x as the product.
We denote the square root of a number x by ![]()
Clearly, ![]()
Square Root of a Perfect Square by the Prime Factorization method:
When a given number is a perfect square, we can find its square root by the following steps:
Step 1. Write prime factors of the given number.
Step 2. Make pairs of similar factors.
Step 3. From the product of the prime factors, choose one factor out of every pair.
ILLUSTRATIVE EXAMPLES
Example: Find the square root of 256.
Solution:
By prime factorization, we get
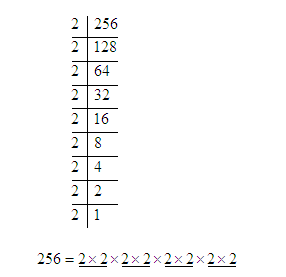
Choose one number from each pair = 2 × 2 × 2 × 2 =16
Example: Find the square root of 1936.
Solution:
By prime factorization, we get
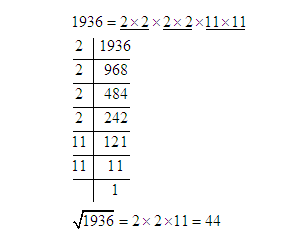
Application of Square Roots To Questions:
Example: In an auditorium, the number of rows is equal to the number of chairs in each row. If the capacity of the auditorium is 2116, find the number of chairs in each row.
Solution: Let the number of chairs in each row be n.
Then, the number of rows = n.
Total number of chairs in the auditorium = (n × n) = n2
The capacity of the auditorium =2116
![]()
Prime factorize it
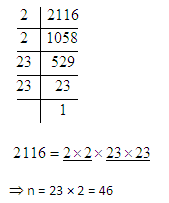
Hence, the number of chairs in each row = 46.
Square Root of A Perfect Square By The Long-Division Method:
When numbers are very large, the method of finding their square roots by factorization becomes lengthy and difficult. So, we use the long-division method, which is explained with the help of examples.
Long-Division Method for Finding Square Roots:
Let us understand the method by taking some examples.
Example1: Find the square root of 256 by the long-division method.
Solution:
Step 1: Make groups of the digits in pairs, starting with the digit in the units place. Each pair and the remaining digit (if any) is called a period.
Now, think of the largest number whose square is equal to or just less than the first period. Take this number as the divisor and also as the quotient, which is 1 in this case
Then subtract the product of the divisor and the quotient from the period.
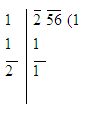
Step 2: Bring down the next period to the right of the remainder. This becomes the new dividend.
Now, the new divisor is obtained by taking two times the quotient and annexing with it a suitable digit which is also taken as the next digit of the quotient, chosen in such a way that the product of the new divisor and this digit is equal to or just less than the new dividend.
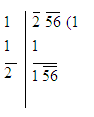
Step 3: Repeat the previous steps till all the periods have been taken up. Now, the quotient so obtained is the required square root of the given number.
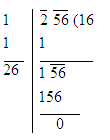
Hence square root of 256 is 16
Example 2: Evaluate ![]() using long-division method.
using long-division method.
Solution:
Marking periods and using the long-division method, we have:
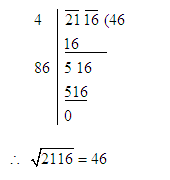
Square Roots of Numbers In Decimal Form:
Method: Make the number of decimal places even by affixing a zero, if necessary. Now, mark periods just like the process elaborated before and find out the square root by the long-division method. Put the decimal point in the square root as you start working with the period just after decimal.
Example: Evaluate ![]()
Solution:
Using the division method we may find the square root of the given number as shown below.
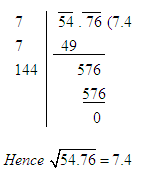
Example: Evaluate ![]()
Solution:
Using the division method we may find the square root of the given number as shown below.
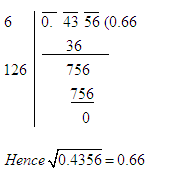
To Find The Value of Square Root Correct Up To Certain Places of Decimal
If the square root is required correct up to two places of decimal, we shall find it up to 3 places of decimal and then round it off up to two places of decimal.
Similarly, if the square root is required correct up to three places of decimal, we shall find it up to 4 places of decimal and then round it off up to three places of decimal, and so on.
We can understand it by following examples.
Example 1: Evaluate ![]() correct up to two places of decimal.
correct up to two places of decimal.
Solution : Using the division method we may find the value of ![]() as shown below.
as shown below.
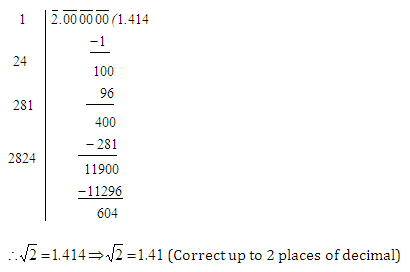
Example 2: Evaluate ![]() correct up to two places of decimal.
correct up to two places of decimal.
Solution:
Using the division method, we may find the value of![]() as shown below.
as shown below.

Square Roots of Fractions:
For any positive numbers a and b, we have:
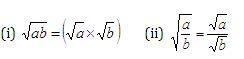
Let us go through a few examples to understand the concept better.
Example 1: Evaluate ![]()
Solution: We have![]()
By prime factorization method
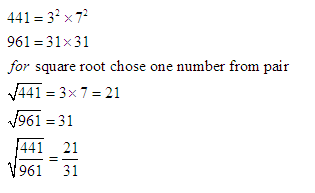
Example 2: Find the square root of ![]() .
.
Solution:

Exercise :-
Question 1: 
Answer and Explanation
Solution (3)
Calculate square root by long division method
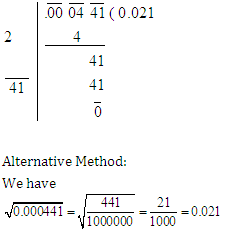
Question 2: 
Answer and Explanation
Solution (2)
We have
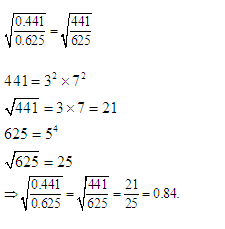
Question 3: ![]()
Answer and Explanation
Solution (2)
We have
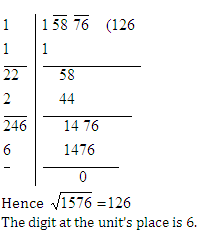
Question 4: The smallest 4-digit number, which is a perfect square, is
(1) 1009
(2) 1016
(3) 1024
(4) 1025
Answer and Explanation
Solution (3)
This question is based on hit and trial
The smallest 4-digit number = 1000
The smallest 4 digit perfect square number = 210 = 1024.
Question 5: The number of perfect square numbers between 50 and 1000 is
(1) 21
(2) 22
(3) 23
(4) 24
Answer and Explanation
Solution (4)
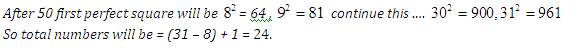
Question 6: 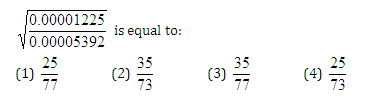
Answer and Explanation
Solution (2)
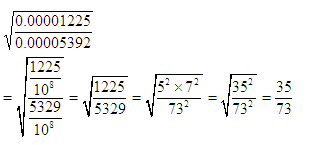
Question 7: 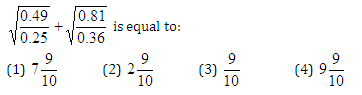
Answer and Explanation
Solution (2)
We have
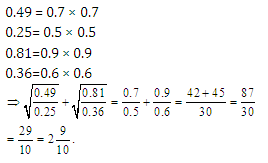
Question 8: 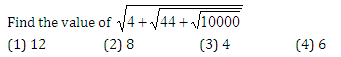
Answer and Explanation
Solution (3)
We have
![]()










