SQUARES & SQUARE ROOTS
Before starting with this concept, you should know how important this concept is.
In Quant and DILR section of CAT or any other MBA entrance exam, there are questions which involve intense calculations. That is where squares and square roots come in handy. Therefore, it’s important for you to know this concept in detail. Let us start digging into it!
Square of a number:
Square of a number means to multiply the number with itself. Square of a number “a” will be equal to ![]() . According to the definition:
. According to the definition:![]()
For example:
22 = (2× 2) =4 and we say that the square of 2 is 4.
Similarly, 52 = (5 × 5) = 25 and we say that the square of 5 is 25.
Perfect Squares Or Square Numbers:
A natural number is called a perfect square or a square number if it is the square of some natural number.
Example: We know that 1=12; 4=22; 9=32; 16=42; 25=52, and so on.
Thus 1, 4, 9, 16, 25, etc., are perfect squares.
Properties To Check If A Number Is A Perfect Square
NOTE: These properties do not make sure whether a given number is a perfect square but they can definitely tell if a number is not a perfect square.
- A number ending in 2, 3, 7 or 8 is never a perfect square. Vice versa we can say that perfect square numbers end in 0,1,4,5,6,9.
The numbers 82, 93, 187, 248 end in 2, 3, 7, and 8 respectively.
So, none of them is a perfect square.
- If unit digit ends in 5, ten’s digit is always 2.
- If unit digit ends in 6, ten’s digit is always odd (1, 3, 5, 7, and 9) otherwise it is always even. That is if a number ends in 1, 4, and 9 then it’s ten’s digit is always even (2, 4, 6, 8, 0).
- A number ending with odd number of zeros is never a perfect square. Think it this way, to make a perfect square you will multiply a number to itself. So, after multiplication you cannot have odd number of zeroes.
Example:
The numbers 160, 4000, 900000 end in one zero, three zeros and five zeros respectively.
So, none of them is a perfect square.
- If a number when divided by 3 leaves a remainder 2, then it can never be a perfect square. If a number when divided by 3 gives a remainder of 0, 1 then it is not necessarily a perfect square but it can be a perfect square.
- If a number when divided by 4 leaves a remainder 2 or 3, then it can never be a perfect square. If a number when divided by 4 gives a remainder of 0,1 then it is not necessarily a perfect square but it can be a perfect square.
- The square of an even number is always even and the square of an odd number is always odd.
Example:
22 = 4, 42 = 16, 62 = 36, 82 = 64, etc.
12 = 1, 32 = 9, 52 = 25, 72 = 49, 92 = 81, etc.
Concept of digital root:
To find digital root of a number, add all the digits of a number.
If the sum is more than 9, add the digits of sum and keep repeating the process until you get a single digit.
Example: What is the digital root of 213?
Solution: Add digits of the number.
2+1+3=6 => so digital root is 6.
Example: what is the digital root of 213457?
Solution:
Add digits of the number
2+1+3+4+5+7=22
Add digits of 22
2+2= 4 => so digital root is 4
Note: If a number is a perfect square, it will always have a digital root of 1,4,7 or 9.
Now the question is how does this help in finding out a perfect square? Let us understand how we will use the above-discussed properties.
(Please remember these properties make sure which number is NOT a perfect square. You cannot say about being a perfect square surely. )
TEST 1
- Perfect square should end in digits 0,1,4,5,6,9. If a number is ending in zero, there should be even number of zeroes.
- If a number is perfect square, it will always have a digital root of 1, 4, 7 or 9.
Example: Is the number 14726 a perfect square?
Solution:
Step 1: As number is ending in digit 6 it can be a perfect square according to property a .
Step 2: Digital root:
Add the digits => 1+4+7+2+6 =20
Add again => 2+0=2
According to property b, a perfect square always have digital root of 1,4,7,9 but this number has a digital root of 2.
So, this is not a perfect square.
Example: Is the number 1472637659872 a perfect square?
Solution:
Considering property a, we know that a perfect square will always end in digits 0,1,4,5,6,9. But this number is not ending in any of these digits, so the given number is not a perfect square.
Example: Is 133581389 a perfect square?
Solution:
Considering property a, we know that a perfect square will always end in digits 0,1,4,5,6,9. So, this number can be a perfect square. We also know that if a number is ending in digit 9, its penultimate digit has to be even. In this case it is 8. So it qualifies both the conditions.
Now we have to check for digital root.
Add the digits 1+3+3+5+8+1+3+8+9 =41
Add again 4+1 =5
So digital root is 5
We know that if a number is perfect square, it will always have a digital root of 1, 4, 7 or 9, but in this case it is 5, so it is not a perfect square.
TEST 2
A perfect square number is always expressible as the product of pairs of equal factors.
Example: Is 256 a perfect square? If so, find the number whose square is 256.
Solution:
Resolving 256 into prime factors, we get
256 =![]()
Thus, 256 can be expressed as a product of pairs of equal factors.
256 is a perfect square.

So, 256 is square of 16.
Example: Show that 1215 is not a perfect square.
Solution: Resolving 1215 into prime factors, we get
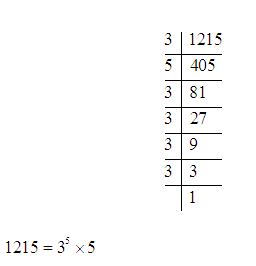
It cannot be expressed as product of pairs. So, 1215 is not a perfect square.
NOTE: This method exactly tells if number is perfect square or not. Question arises why do we use Test 1 then. In case of big numbers Test 2 takes time, so we first apply test 1 and reduce choices.
Some Important Properties of Perfect Squares
- The square of a proper fraction is smaller than the fraction.
Example: 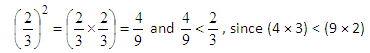
- For every natural number n, we have
(n + 1)2 – n2 = (n + 1 + n) (n + 1 – n) = {(n + 1) + n)
![]()
Example:
- {(36)2 – (35)2} = (36+35) = 71
- (ii) {(89)2 – (88)2} = (89+88) = 177.
- For every natural number n, we have
Sum of first n odd natural numbers = n2.
Example:
(i) {1 + 3 + 5 + 7 + 9} = sum of first 5 odd numbers = 52.
(ii) {1+3+5+7+9+11+13+15} = sum of first 8 odd numbers = 82.
- (Pythagorean Triplets): Three natural numbers a, b and c are said to form a Pythagorean triplet (a, b, c) if a2 + b2 = c2.
For every natural number a > 1, we have (2a, a2 – 1, a2 + 1) as a Pythagorean triplet.
Example:
(i) Putting a =4 in (2a, a2 – 1, a2 + 1), we get (8, 15, 17) as a Pythagorean triplet.
(iI) Putting a = 5 in (2a, a2 – 1, a2 + 1), we get (10, 24, 26) as a Pythagorean triplet.
- Between two consecutive square numbers n2 and (n + 1) 2, there are 2n non-perfect square numbers.
Example: If n= 2 then
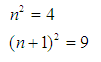
And we have 2n i.e. 4 non perfect numbers between them which are 5, 6, 7, 8.
EXERCISE
Q1. Is the number 10609 a perfect square?
Answer and Explanation
Solution: We can use either test 1 or test 2 . Let us try both.
Test 1:
If a perfect number ends with 9 its 10’s digit has to be even. 10609 fulfill the condition.
Digital sum = 1+0+6+0+9=16
1+6= 7
If a number is perfect square, it will always have a digital root of 1,4,7 or 9.
So, it can be a perfect square.
To be sure we have to take test 2
Test 2:
Prime factorize the number
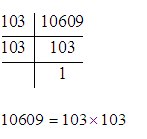
It can make a pair of two numbers so it is a perfect square.
Q2. Calculate {(43)2 – (42)2}
Answer and Explanation
Solution: Use formula ![]()
42+1+42=85
Q3. Prime factorize 1317120
Answer and Explanation
Solution:
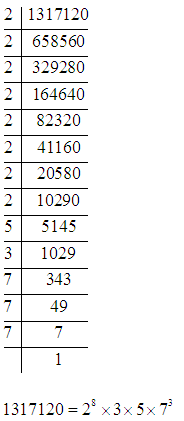
Q4. Is the number 147784689503 a perfect square?
Answer and Explanation
Solution: A number ending in 2, 3, 7 or 8 is never a perfect square. So this number is not a perfect square.
NOTE: By using test 1, you don’t need to prime factorize this big number.
Q5. Is the number 2837325 a perfect square?
Answer and Explanation
Solution: This number is not ending in 2,3,7,8 so this can be a perfect square. Let us calculate it’s digital root.
Add digits = 2+8+3+7+3+2+5 =30 = 3 + 0 = 3
If a number is perfect square it’s digital root has to be 1,4,7,9, but digital root of this number is 3. So this number cannot be a perfect square.







