In the previous articles, we learnt about an irrational number. But what is a Surd?
In this article we will get to know more about Surds and its applications.
Definition: An irrational number with root (square root, cube root, etc.) is called a surd. For example:
, etc.
Alternatively, when we can’t simplify a number to remove the root (square root, cube root, etc.), then it called a surd.
For example: , etc. cannot be simplified to remove the root. Hence, they are surds.
Note: Not all roots are surds.
For example: can be simplified to remove root. Therefore, it is not a surd. (As
=2)
Let us try understanding surds more closely,
If x is a positive rational number, then
root of x will be
. This is called a surd, where n is order of surd and x is positive rational number.
It can be noted that the operations applied in surds are basically opposite of that applied in exponents.
In exponents,
While in surds,
For example,
(As we know )
Which makes it =>
So, 
=3
That is why we say operation in surds is the opposite of operation in exponents.
Theory of surds:
It goes back to history in the time of Pythagorean theorem. We all are aware of Pythagorean theorem, which says square of hypotenuse is equal to sum of square of base and perpendicular.
Pythagorean theorem:
Consider a right angle triangle with base and perpendicular of 1 unit.
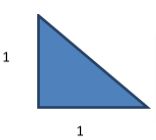
Using Pythagorean theorem,
It comes out to be root 2, which is a surd.
Rationalization in surds:
Rationalization is done in order to remove surd (or say, Root) from denominator to make calculation easier. Let us understand this with the help of examples.
Example 1: Rationalize
.
Solution:
As we want to rationalize , we have to make the denominator a rational number. Hence, we will multiply and divide the fraction by 
Hence, we have 
Let us take another example.
Example 2:
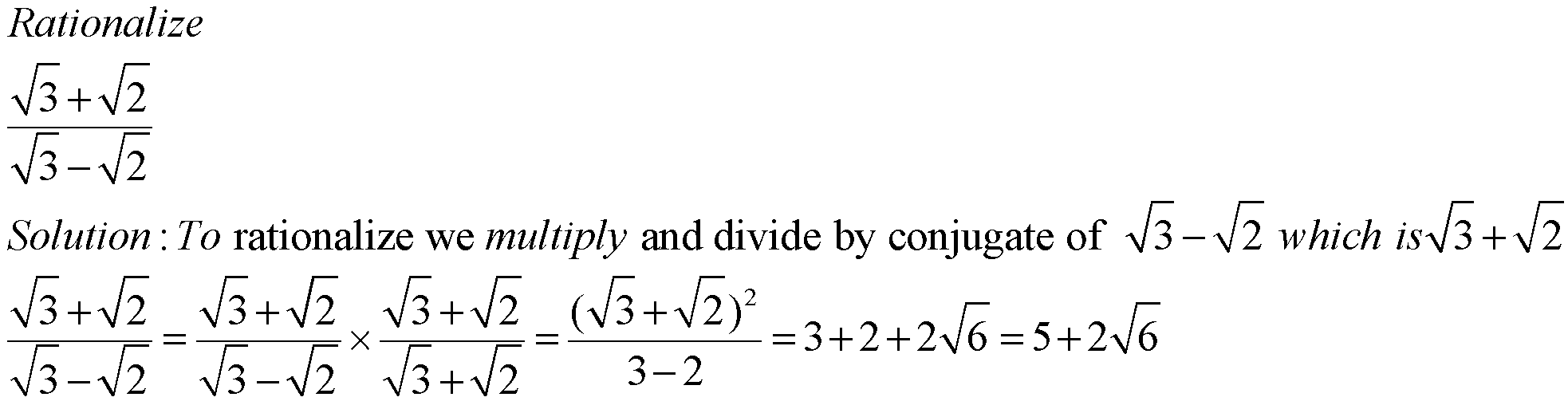
Operations in surds:
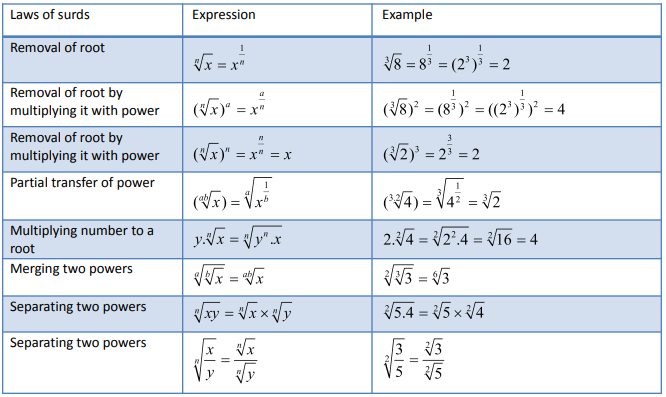
To understand surds more, take a look at the laws of surds given in the table below:
Comparison of surds:
It gets tricky to compare surds as it there isn’t a precise value and it needs judgment to make a quick and easy comparison.
You could refer the below cases to get quick with comparisons:
Case 1. When the power is same
When we have
if x>y
if x<y
Example 1: Which is greater ?
Solution: because 5>4 (as the power here in both options is same)
Example 2: Which is greater ?
Solution: because 8 > 7 (as the power here in both options is same)
Case 2. When power is not same
Step 1: First, we make the denominator of the power same, which is equal to the LCM of the denominators of powers, by multiplying and dividing by a suitable number.
Step 2: Then use the concept used in case 1.
Example 1: Which is greater
Solution:
LCM of denominators of powers is = LCM (3, 4) = 12. Now, we will make the denominators of powers equal to 12.
Example 2: Write following in descending order: .
Solution:
Lcm of denominators of power 3,4 and 12 is 12 .
So, to convert power into same order, we make the denominators of powers equal to 12.
Exercise :
