‘Time and work’ is a topic from which a lot of questions are asked in the competitive examinations.
Generally, questions are related to the men doing work individually and the time required in doing the same work together. Then there will be some questions where a group of people starts the work and after some time, some of them leave the work and you are asked to calculate the time required for the remaining persons to complete the work. But how do you go about solving such scenarios? Refer to this article for it!
You will learn how to solve different types of problems related to chapter time and work. But before starting with the types of problems, we will learn some basics about the topic.
Concept:
In time and work problems, we assume that the work done by the persons is same on each day unless it is specified in the question that they are doing the work with different rates on different days.
Example 1: Let a person A can do the work in 10 days. It means that each day he will do 1/10th of the work. Let another person B can do the same work in 15 days, so B can do 1/15th of the whole work every day. Now, if we employee both A and B to the work then in how many days the work will be completed?
Solution:Well!! In time and work problems you just keep two things in mind. First, that every person is doing his own work and second, for how many days each person is working.
Here if we employ A and B to do the work then in one day, A will do his own 1/10th part of the work and B will do his own 1/15th part of the work. So together they will do ![]() of the total work in one day. Now as they are doing 1/6th of the work in one day, so the total time taken by them will be 6 days.
of the total work in one day. Now as they are doing 1/6th of the work in one day, so the total time taken by them will be 6 days.
In this example we took the whole work as one unit.
There is another approach to solve these questions where fractions are not involved. In that case we take the whole work that is exactly divisible by the total days taken by A and B individually which is normally the LCM of the days.
So,in the above example, the LCM of 10 and 15 is 30, so let the total work is 30 units.
Now as A completes the work in 10 days, so he is doing 3 units work per day. Similarly, B is doing 2 units of the work daily. Together they will do 5 units of work daily.
So, to complete the whole 30 units, they will take 30/5 = 6 days.
Now let us see another problem.
Example 2: Let A and B can do a work in 15 days and 20 days,respectively. Both started the work together. After 6 days, A left the work. In how many days B will complete the remaining work?
Solution: Here A and B can do 1/15th and 1/20th work in one day working independently.
So together they will do![]() work in one day.
work in one day.
As they did the work together for six days, so in 6 days they will do ![]() of the total work.
of the total work.
Now, the remaining ![]() work will be done by B alone. B can do 1 unit work in 20 days, so he will do 3/10th work in
work will be done by B alone. B can do 1 unit work in 20 days, so he will do 3/10th work in ![]()
Let us try this question with the other method where the work is not 1 unit but a common multiple of the number of days. Let the total work = LCM (15, 20) = 60 units.
So, A can do 4 units in a day and B can do 3 units in a day. Together they can do 7 units in one day.
As they worked together for 6 days, so in six days they will do 7 × 6 = 42 units.
The remaining work is 60 – 42 = 18 units which will be done by B alone and as he can do 3 units in a day so he will take 18/3 = 6 days to complete it.
Note: In these questions you should be careful about what is asked. Whether the question is asking about the number of days to complete the remaining work or to complete the whole work? If in the above question we were asked to calculate the number of days required to do the whole work, then the answer would be 6 + 6 = 12 days (6 days when they worked together and 6 days when B worked alone)
Example 3: Let A and B can do a work in 20 days and 30 days, respectively. B started the work. After how many days A should join the work so that the work completes in 15 days?
Solution: Let the total work is LCM (20, 30) = 60 units.
So, A can do 3 units per day and B can do 2 units per day.
Now we want to complete the work in 15 days and B has already started the work. It means that B will work for full 15 days (Remember you must keep in mind that every person is doing his work and for how many days he is doing).
So, he will do 15 × 2 = 30 units in 15 days.
The remaining work is 60 – 30 = 30 units which will be done by A.
As A can do 3 units so he will take 30/3 = 10 days. It means that A worked for 10 days.
As the total works is completed in 15 days and A worked for only 10 days, so he should join after 15 – 10 = 5 days.
Hope that the above examples have made the concept clear to you all.
Now sometimes instead of the number of days the efficiency of the persons is given in the questions. Let us see how it works.
If A is twice as efficient asB, then you can take its meaning in two ways.
(i) At the same time, A will do twice the work done by B.
(ii) If the work is constant, then A will take half the time taken by B to complete it.
Let us see an example.
Example 4: A is twice efficient than B and together they can do a work in 30 days. In how many days they will do the work individually?
Solution: In this question, the work is constant.
As A is twice efficient than B so he will take half time than B.
Let the time taken by A alone is ‘x’ days and by B alone is ‘y’ days.
Together they take 30 days to complete the work.
So, we have ![]()
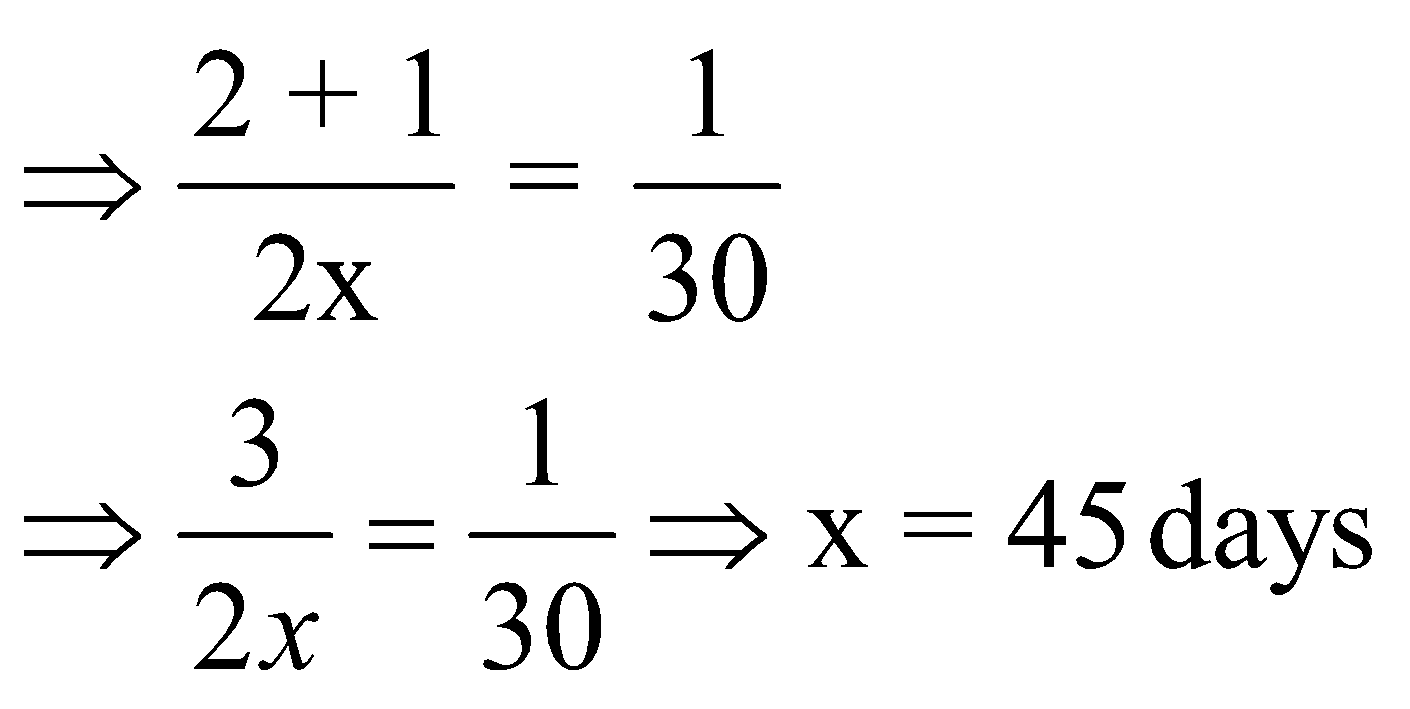
So, A can do the work individually in 45 days and B can do it in 2x = 2 × 45 = 90 days.
This question can also be solved by another method:
Since A is twice efficient than B, so let us say that A can do 2 units work in one day and B can do 1 unit work in 1 day. Together they will do 3 units in a day.
Now as the work is completed in 30 days, so the total work = 30×3 = 90 units.
So, A alone will take 90/2 = 45 days and B alone will take 90/1 = 90 days to complete it.
You can also use the following concepts that can directly help you to solve the question.
Concept 1:
If A can do a piece of work in x days and B can do it in y days, then A and B working together will do the same work in 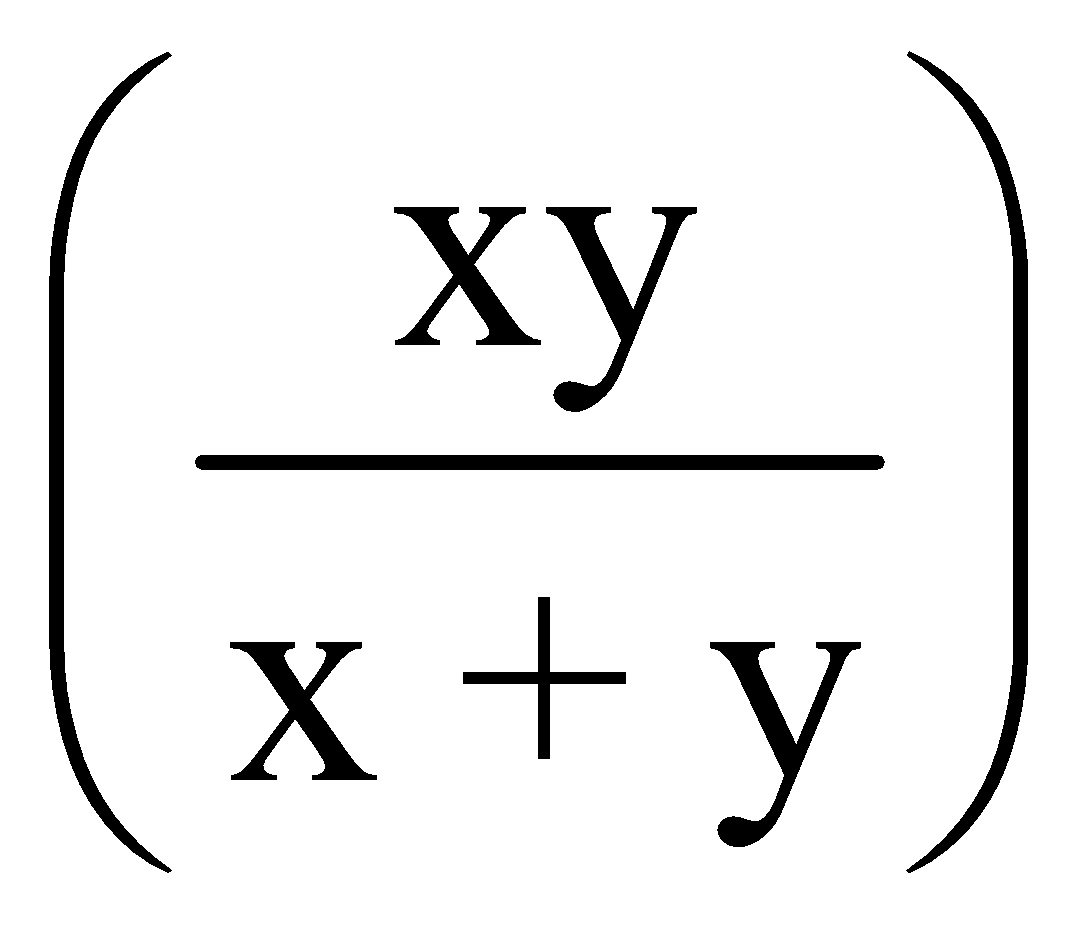 days.
days.
Derivation:
If A can do 1 work in x days,then,
In 1 day, work done by A will be =![]()
If B can do 1 work in y days, then,
In 1 day, work done by B will be =![]()
Their combined work in 1 day =![]() of total work =
of total work = ![]() of total work
of total work
Total time taken to do the work =![]()
Concept 2:
If A,B, and C can do a work in x,y, and z days respectively then all of them working together can finish the work in 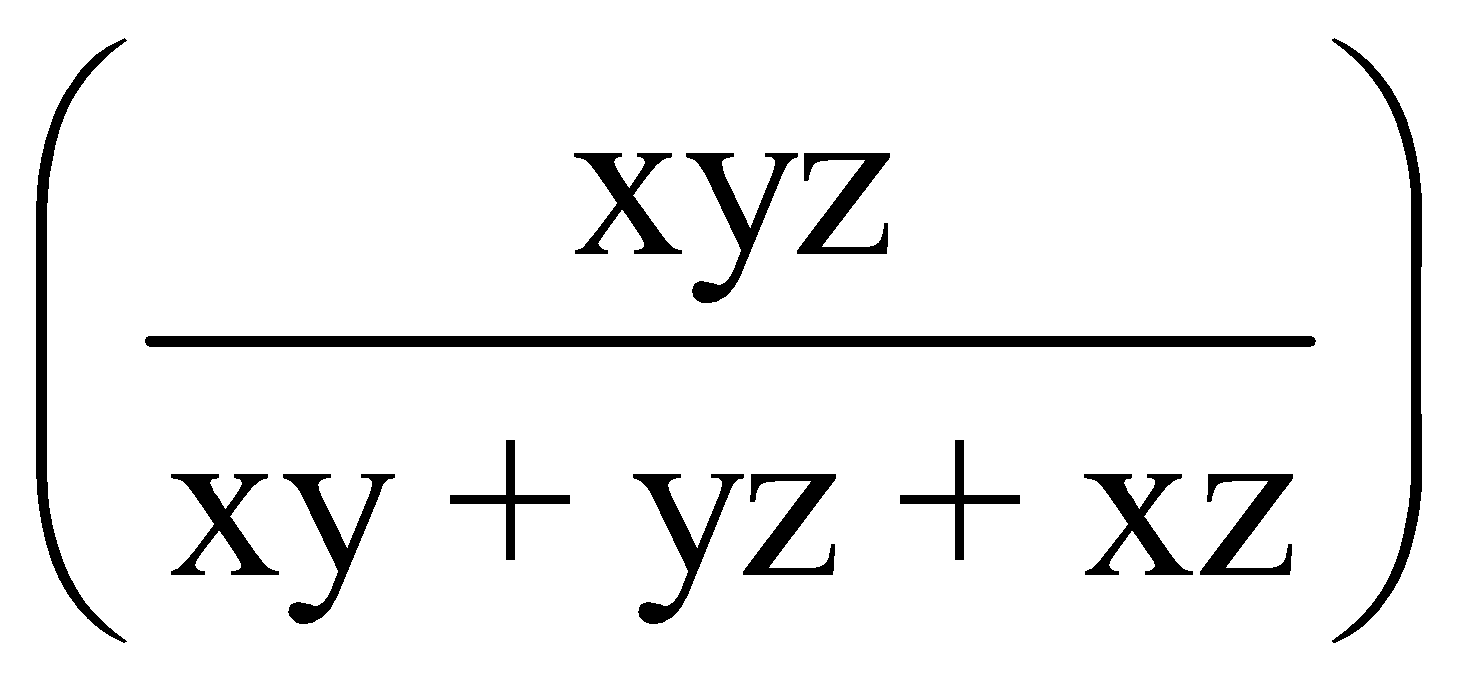 days.
days.
Example 5: A can do a piece of work in 6 days and B can do it in 5 days. How long will it take if both work together?
Solution: Using the formula, the number of days =![]()
Example 6: A can do a piece of work in 6 days, B can do it in 12 days, and C can do it in 5 days.How long will they take to complete the work?
Solution: Using the formula, the number of days =![]()
Concept 3:
If A and B together can do a piece of work in m days and A alone can do it in ndays,then B alone can do the work in![]()
Derivation:
(A+B)’s 1 day work =![]()
A’s 1 day work =![]()
B’s 1 day work= 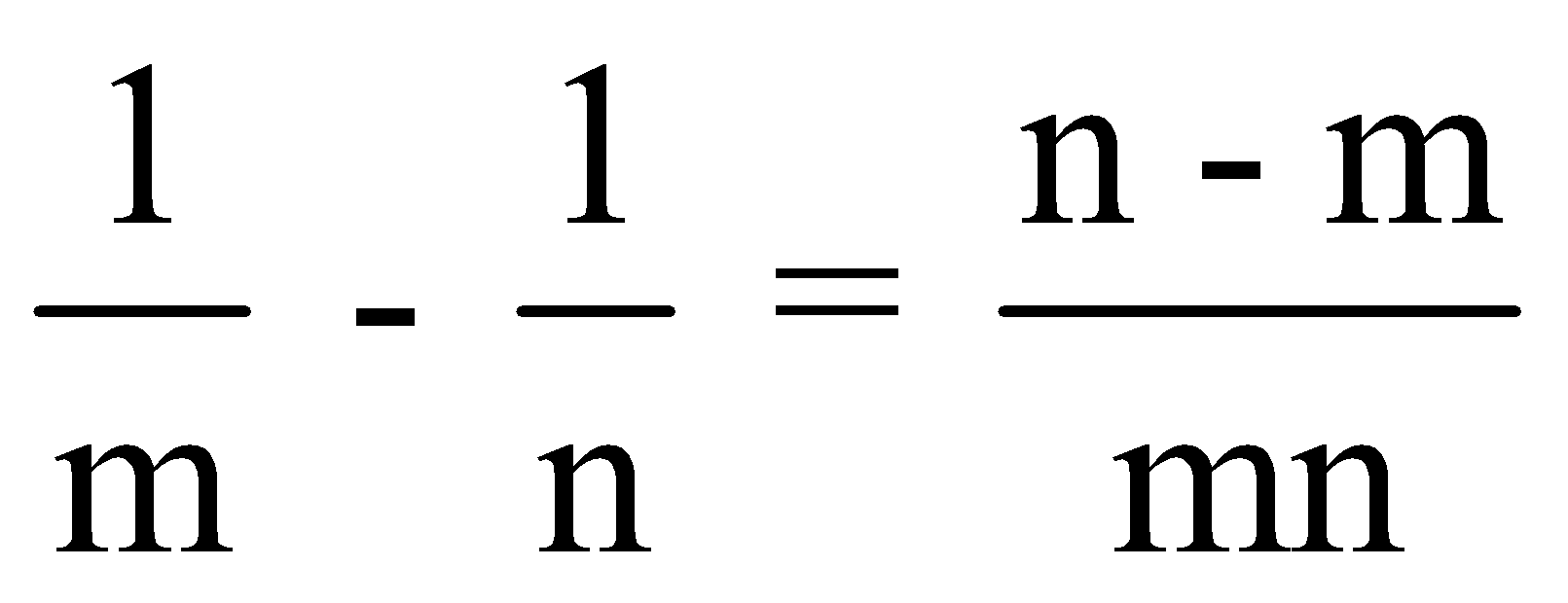 of total work
of total work
Time taken to do total work =![]()
Example 7: A and B together can do a piece of work in 9 days and A alone can do it in 12 days. In how many days B alone can do it?
Solution: Using the formula the required time taken by B =![]()
EXERCISE:
Question 1: A and B can do a piece of work in 72 days. B and C can do it in 120 days. A and C can do it in 90 days. In how many days all the three together can do the work?
(1) 80 days
(2) 100 days
(3) 60 days
(4) 150 days
Answer and Explanation
Solution: (3)
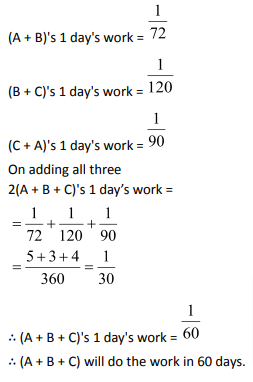
Question 2: A and B can do a piece of work in 10 days, B and C in 15 days and C and A in 20 days. C alone can do the work in:
(1) 60 days
(2) 120 days
(3) 80 days
(4) 30 days
Answer and Explanation
Solution: (2)
According to the question,
Work done by (A+ B) in one day = ![]() part of work
part of work
Work done by (B+ C) together in one day =![]() part of work
part of work
Work done by (C + A) together in one day =![]() part of work
part of work
By adding all the equations
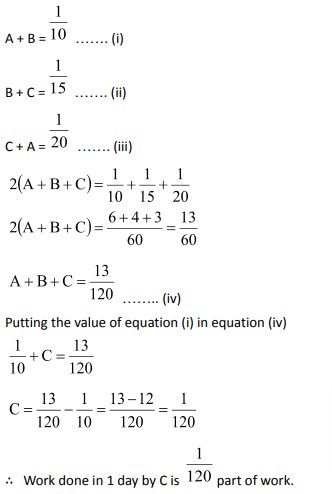
Hence, C will finish the whole work in 120 days.
Question 3: A can do a piece of work in 4 hours; B and C can do it in 3 hours; A and C can do it in 2 hours. How long will B alone take to do it?
(1) 10 hours
(2) 12 hours
(3) 8 hours
(4) 24 hours
Answer and Explanation
Solution: (2)
A can do 1 work in 4 days.
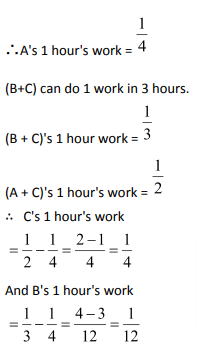
Hence, B alone can do the work in 12 hours.
Question 4: While working 7 hours a day, A alone can complete a piece of work in 6 days and B alone in 8 days. In what time would they complete it together, working 8 hours a day?
(1) 3 days
(2) 4 days
(3) 2.5 days
(4) 3.6 days
Answer and Explanation
Solution: (1)
A alone can complete the work in 42 days working 1 hour daily.
Similarly, B will take 56 days working 1 hour daily.

Question 5: Ronald and Elan are working on an Assignment. Ronald takes 6 hours to type 32 pages on a computer, while Elan takes 5 hours to type 40 pages. How much time will they take working together on two different computers to type an assignment of 110 pages?
(1) 7 hrs. 30 min.
(2) 8 hrs.
(3) 8 hrs. 15 min.
(4) 8 hrs. 25 min.
Answer and Explanation
Solution: (3)
Ronald takes 6 hours to type 32 pages.
Roland’s 1 hour’s work ![]() pages.
pages.
Elan takes 5 hours to type 40 pages.
Elan’s 1 hour’s work = 8 pages.
1 hour’s work of both:
![]()
pages
To type ![]() pages, they take 1hr.
pages, they take 1hr.
To type 110 page, they will take![]() hours= 8 hours 15 minutes
hours= 8 hours 15 minutes
[/learn_more
Question 6: A and B can do a work in 18 and 24 days, respectively. They worked together for 8 days and then A left, the remaining work was finished by B in:
(1) 5 days
(2) 5![]() days
days
(3) 8 days
(4) 10 days
Answer and Explanation
Solution: (2)
A’s one day’s work =![]()
B’s one day’s work![]()
(A + B)’s 1 day work =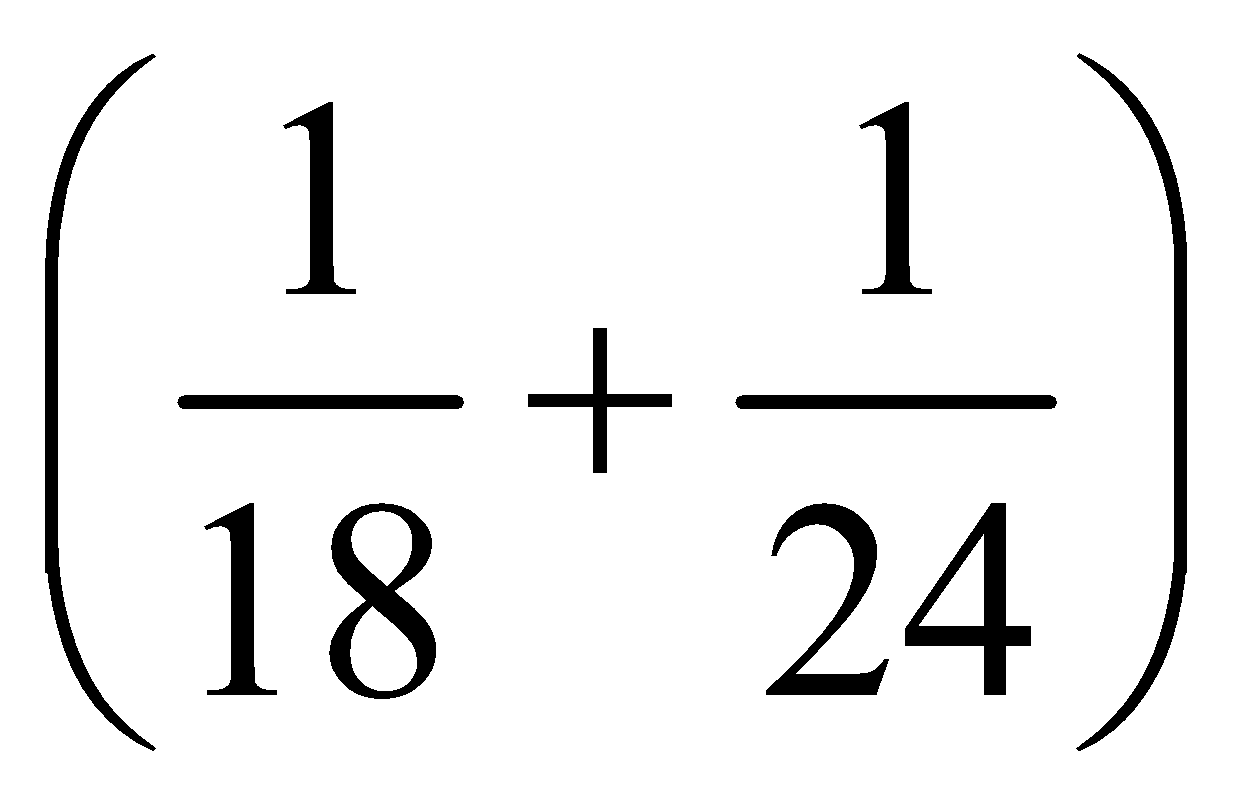
(A + B)’s 8 day’s work![]()
As we consider total work as 1
∴ Remaining work =![]()
This will be done by B.
∴ Time taken by B to finish ![]() of work =1 day
of work =1 day
Time taken by B to finish ![]() of work =
of work =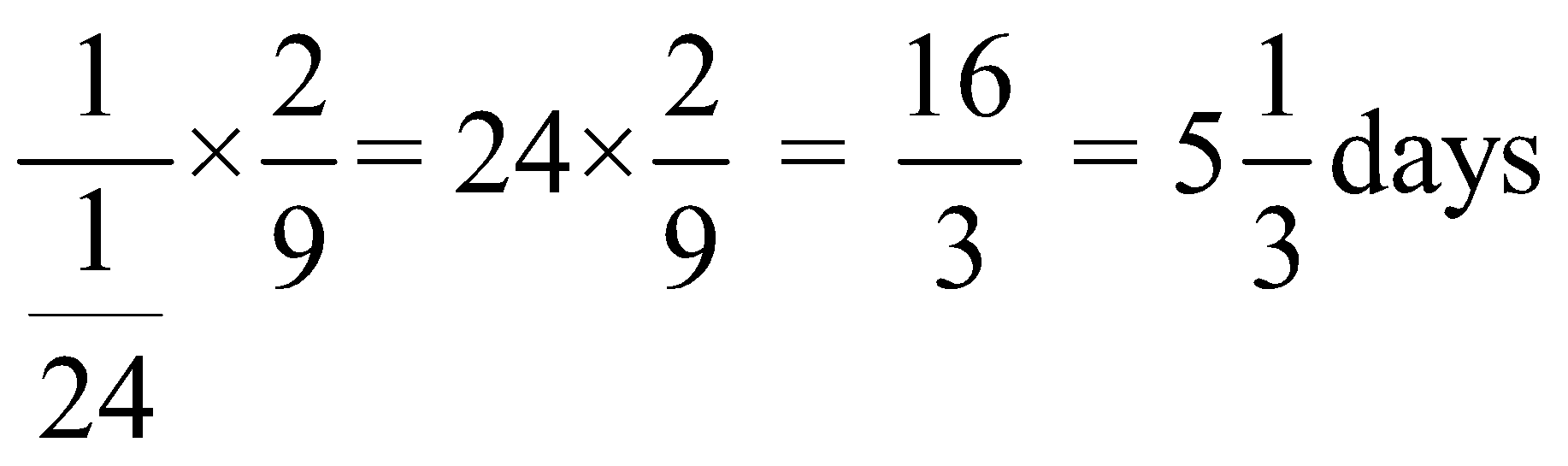
Question 7: A and B can do a piece of work in 28 and 35 days respectively. They began to work together but A leaves after some time and B completed remaining work in 17 days. After how many days did A leave?
(1) 14 ![]() days
days
(2) 9 days
(3) 8 days
(4) 7 ![]() days
days
Answer and Explanation
Solution: (3)
Let A worked for x days.
A’s 1 day work= ![]() of work
of work
B’s 1 day work= ![]() of work
of work
B works for (x+17) days so
According to the question (A+B)’s combined work will add up to 1
![]()
⇒![]()
⇒ 5x + 4x + 68 = 140
⇒ 9x = 140 – 68 = 72
⇒ x = 8
∴ A worked for 8 days.
Question 8: A man and a boy can complete a work together in 24 days. If for the last six days man alone does the work, then it is completed in 26 days. How long the boy will take to complete the work alone? (1) 72 days
(2) 20 days
(3) 24 days
(4) 36 days
Answer and Explanation
Solution: (1)
Suppose a man can complete the work in x days and a boy can complete in y days.
1 day work for a man =![]()
1 day work for a boy =![]()
They can complete it together in 24 days.
In 24 days, man’s work =![]()
In 24 days, boy’s work =![]()
Combined work
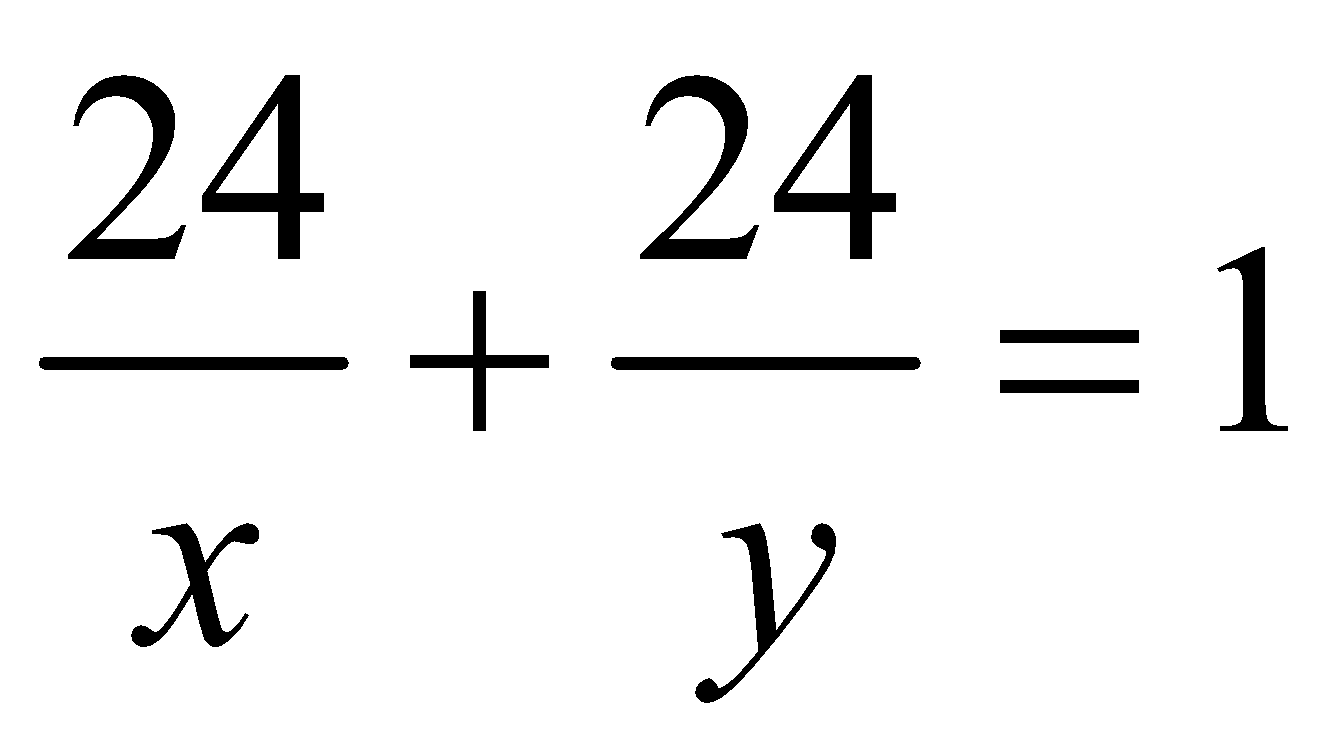 ….. (1)
….. (1)
![]() …… (2)
…… (2)
Solving the two equations together,we get y = 72 days.
Question 9: A and B together can complete a work in 8 days. B alone can complete that work in 12 days. B alone worked for four days. After that how long will A alone take to complete the work?
(1) 15 days
(2) 18 days
(3) 16 days
(4) 20 days
Answer and Explanation
Solution: (3)
Apply formula: –
Time taken by A to do 1 work =![]()
Here, m = 8 and n=12
So the required time = ![]() =24 days
=24 days
Work done by B in one day =![]() th of work
th of work
Work done by B in 4 days =>![]() rd of work
rd of work
Remaining work
![]() part
part
A can complete a work in 24 days.
A can complete![]() part of work in
part of work in ![]() = 16 days
= 16 days
Question 10: A, B and C can do a piece of work in 10, 12 and 15 days respectively. A leaves 5 days before the completion of the work and B leaves 2 days after A. The whole work lasts for
(1) 6 days
(2) 12 days
(3) 13 days
(4) 7 days
Answer and Explanation
Solution: (4)
Required time to complete the work is x.
And all will add up to do 1 work.
∴![]()
⇒![]()
⇒ 15x – 45 = 60
⇒ 15x = 105
⇒ x = 7 days
Time and WorkQuestions: Problems on Time and Workyou should solve for competitive examination preparation
Welcome to this exercise on Time and Work problems. In this exercise, we build on the basic concepts for Time and Work. As you prepare for your competitive examinations, you will come across questions on Time and Work. Such questions need optimized tackling and can be solved with ease by using simple tricks and understanding the relationships highlighted in this Time and WorkQuestions article. The Time and WorkQuestions exercise comes into the picture where it gives you a chance to practice the highlighted and important concepts related to Time and Workquestion type.













