In the previous article, we covered some important concepts of time and work. Now, we are going to proceed with another important concept of the topic time and work.
Concept:
Sometimes we deal with the questions in which a group of people can do a work in some days and then we are asked to calculate the number of days taken by the second group of the people to do the same work. We can use the following result to solve such questions.
If m1people can do w1work in d1 days working t1 hours daily with efficiency e1 andm2 people can do w2work in d2 days working t2 hours daily with efficiency e2then we have:
![]()
Here in the above equation, the work done by a group is written on the other side of the equation. The reason for this is that the work done is directly proportional to the number of men or the number of days or the number of hours or the efficiency.
If any parameter is not given in the question, then we can directly ignore that parameter from the above equation. E.g., if number of hours and efficiency is not given then the above equation will become:
![]()
Let us understand this by some examples:
Solved Examples:
Example 1: 40 men can do a work in 10 days.How many men are needed to complete the work in 80 days?
Solution:Here m1 = 40, d1 = 10,d2 = 80, m2 =?
We have the result![]()
⇒ 40 × 1 × 10 = m2 × 1 ×80 (Here the work as taken as 1 unit)
⇒ m2 = 5.
Example 2: 40 men can make 60 walls in 8 hours.If 8 men leave the job, how many walls will be made in 12 hours?
Solution:Here we have m1=40; w1=60; t1=8hrs; m2=40-8=32men; t2=12hrs; w2=?
We have m1 t1 w2 = m2 t2 w1
⇒ 40 × 8 × w2 = 32 × 12 × 60
![]()
Example 3: A is four times as fast as B and is therefore able to finish a work in 60 days less than B.Find the time in which they can do it together.
Solution:Use formula: ![]()
d1e1 = d2e2
Let d2 = x,
d1=x-60; e1=4; e2=1
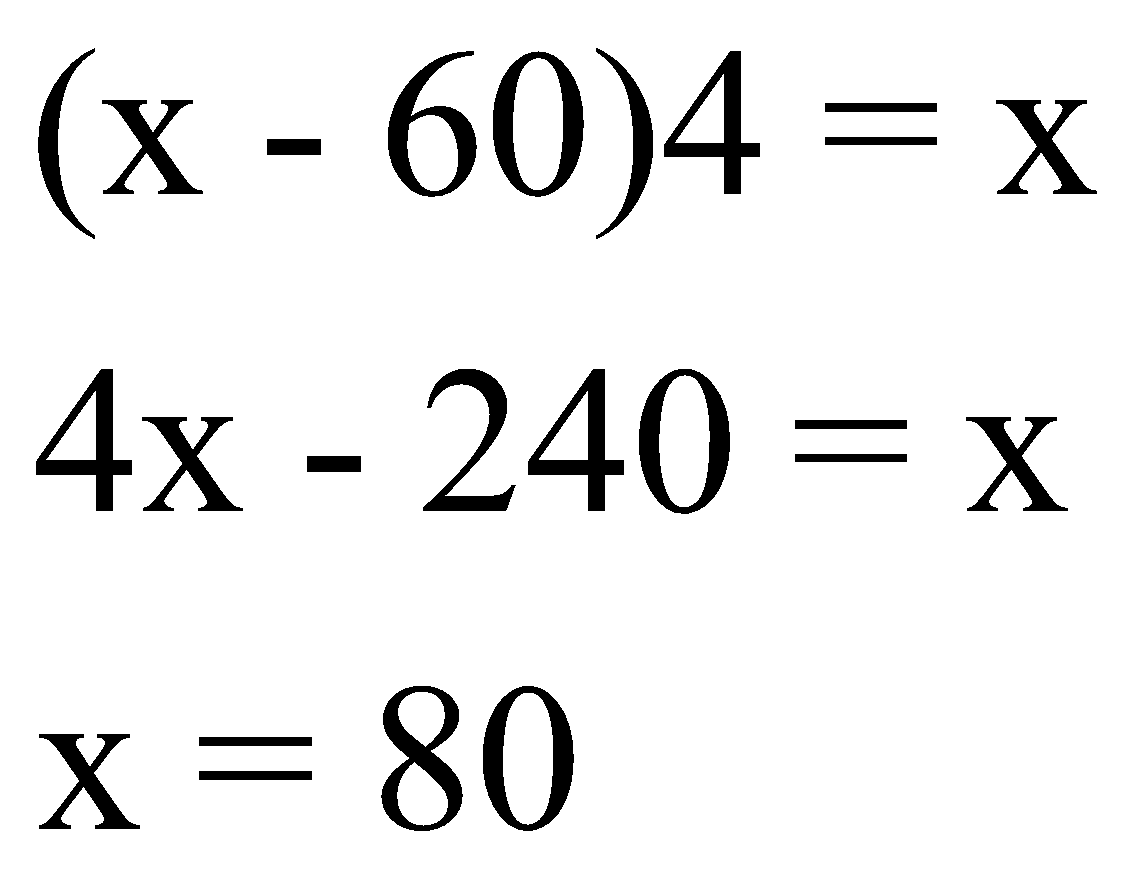
Time taken by A =20 days
Therefore, time taken when they work together =![]() =
= ![]() days
days
Example 4: 8 men can do a work in 12 days. After 6 days of work, 4 more men were engaged to finish the work. In how many days would the remaining work be completed?
Solution:Work done by 8 men in 1 day=![]()
Work done by 8 men in 6 days![]()
Remaining work =![]()
When 4 more men are engaged, Total number of men= 8 + 4 = 12
Applying men-days formula:![]()
![]()
Example 5: In a hostel there is food for 500 students that will last for 40 days. After 10 days 100 more students came. Find the number of days for which the food will last now.
Solution:Here the available food is for 500 students. So, the food will last for 30 more days if no student joins.
But as 100 new students joined, so let the food lasted for ‘x’ days.
Also,now the total number of students becomes 600.
We have M1 D1 = M2 D2 where M1 = 500, M2 = 600, D1 = 30 and D2 = x
⇒500 × 30 = 600 × x
![]()
Example 6: A contractor employed 300 men to complete a work in 150 days. When the work was reviewed after 100 days, he found that only 1/4 work was completed. How many more men are required to complete the work on time?
Solution: Here 300 men had done only 1/4 work in 100 days.
Let after adding the new men, the total number of workers (old + new) is ‘x’.
As the work is to be done on time so the remaining days are 50 in which 3/4of the total work is to be completed. We have
M1 D1 W2 = M2 D2 W1
Þ 300 × 100 × 3/4 = x × 50 × 1/4
![]()
Hence, the new men required = 1800 – 300 = 1500.
Time and Work Questions: Problems on Time and Work you should solve for competitive examination preparation
Welcome to this exercise on Time and Work problems. In this exercise, we build on the basic concepts for Time and Work. As you prepare for your competitive examinations, you will come across questions on Time and Work. Such questions need optimized tackling and can be solved with ease by using simple tricks and understanding the relationships highlighted in this Time and WorkQuestions article. The Time and WorkQuestions exercise comes into the picture where it gives you a chance to practice the highlighted and important concepts related to Time and Workquestion type.







