Previously, we have learned the basics of divisibility and various divisibility checks and rules. In this article, we will learn some shortcuts and tricks for divisibility that will help you solve questions quickly. Without wasting time, let’s get going with the tricks.
Some basics tips and tricks you studied in the previous lessons that you can use for divisibility:
- All whole numbers are divisible by 1.
- A number is divisible by 2 if it is even.
- A non-zero number is divisible by 5 if it ends in 0 or 5.
- In order to check the divisibility of a number by a composite number, divide the composite divisor into prime factors, which are co-prime and then check for its divisibility with each. For example, to check the divisibility of a number with 12, break down 12 into 3 and 4.
Tricks for Divisibility:
- an – bn is always divisible by a-b
Example: 85–55 is divisible by 8-5= 3
Remember it by:
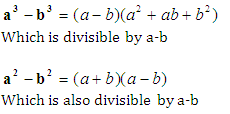
- an – bn is divisible by a + b when n is even
Example: 710 – 510 is divisible by 7-5= 2
Remember it by:
a3 – b3 is not divisible by a + b
a2 – b2 is also divisible by a + b
a4 – b4 is also divisible by a + b
- an + bn is divisible by a + b when n is odd
711 + 511 is divisible by 7 + 5 = 12
Remember it by:
a3 + b3 is divisible by a + b
a2 + b2 is NOT divisible by a + b
a4 + b4 is NOT divisible by a + b
- an + bn + cn is divisible by a + b + c when n is odd.
73 + 53 + 23= 343 + 125 + 8 = 476 divisible by 7 + 5 + 2 = 14
Given below are some questions for you to apply these formulae:
Example 1: 3223 + 1723 is definitely divisible by:
a. 49
b. 15
c. 49 & 15
d. None of these.
Solution: Answer is A
As an + bn is divisible by a + b when n is odd
So 3223 + 1723 is divisible by 32 + 17 = 49.
Example 2: 3223 – 1723 is definitely divisible by:
a. 49
b. 15
c. 49 & 15
d. none of these.
Solution: Answer is B
As an – bn is always divisible by a-b.
So 3223 – 1723 is divisible by 32 – 17 = 15.
Example 3: 32232 – 17232 is definitely divisible by:
a. 49
b. 15
c. 49 & 15
d. none of these.
Solution: Answer is C
As an – bn is always divisible by a-b and an – bn is divisible by a + b when n is even
So 32232 – 17232 is divisible by both 32 – 17 = 15 and 32 + 17 = 49.
Example 4: 35 + 55+ 75 is definitely divisible by:
a. 8
b. 7
c. 15
d. all of these.
Solution: Answer is C
As an + bn + cn is divisible by a + b + c when n is odd.
So 35 + 55 + 75 is divisible by 3 + 5 + 7 = 15
Try out some more questions given in the exercise.
EXERCISE:
Question 1: (49)15 –1 is exactly divisible by:
(1) 50 (2) 51 (3) 29 (4) 8
Answer and Explanation
Solution (4)
By property 1
an – bn is always divisible by a-b
(49)15 –(1)15 is exactly divisible by 49–1 = 48, that is a multiple of 8.
Question 2: If a and b are two odd positive integers, by which of the following integers I (a4 –b4) always divisible?
(1) 3 (2) 6 (3) 8 (4) 12
Answer and Explanation
Solution (3)
an – bn is divisible by a + b when n is even
an – bn is always divisible by a-b
a4 – b4 = (a2 + b2) (a + b) (a – b)
put a=3 , b=1 ( because 1,3 are the smallest odd numbers)
![]() Required number = (3 + 1) (3 – 1) = 8
Required number = (3 + 1) (3 – 1) = 8
Question 3: m and n are positive integers and (m–n) is an even number, then (m2–n2) will be always divisible by
(1) 4 (2) 6 (3) 8 (4) 12
Answer and Explanation
Solution (1)
Let m – n = 2x
m + n = 2x
![]() (m–n) (m+n) = 4x2
(m–n) (m+n) = 4x2
![]() m2–n2 = 4x2
m2–n2 = 4x2
Question 4: It is given that (232 + 1) is exactly divisible by a certain number, which one of the following is also definitely divisible by the same number?
(1) 296 + 1 (2) 7 × 233 (3) 216 – 1 (4) 216 + 1
Answer and Explanation
Solution (1)
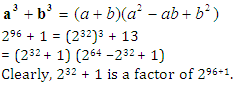
Question 5: The greatest whole number, by which the expression n4 + 6n3 + 11n2 + 6n + 24 is divisible for every natural number n, is
(1) 6 (2) 24 (3) 12 (4) 48
Answer and Explanation
Solution (4)
For n = 1
n4 + 6n3 + 11n2 + 6n + 24
=1 + 6 + 11 + 6 + 24 = 48
For, n = 2
n4 + 6n3 + 11n2 + 6n + 24
=16 + 48 + 44 + 12 + 24
=144 which is divisible by 48.
Clearly, 48 is the required number.







